2.4. Эквивалентные нормы

Определение 13. Пусть в линейном нормированном пространстве с нормой задана еще одна норма . Говорят, что норма подчинена норме , если найдется такая постоянная , что

, . (2.8)

Имеет место теорема.

Теорема 1. Для сходимости по норме любой последовательности, сходящейся по норме , необходимо и достаточно, чтобы норма была подчинена норме .

Доказательство. Достаточность доказывается легко. Действительно, пусть последовательность сходится к элементу по первой норме, т.е. , при . Тогда из (2.8) имеем

,

откуда следует сходимость последовательности к элементу и по второй норме.

Необходимость докажем от противного. Пусть неравенство (2.8) не выполнено. Тогда для любого натурального числа найдется такой элемент , что

.

Обе части этого неравенства поделим на одно и то же число , отличное от нуля, которое затем внесем под знак каждой нормы. В результате получим неравенство

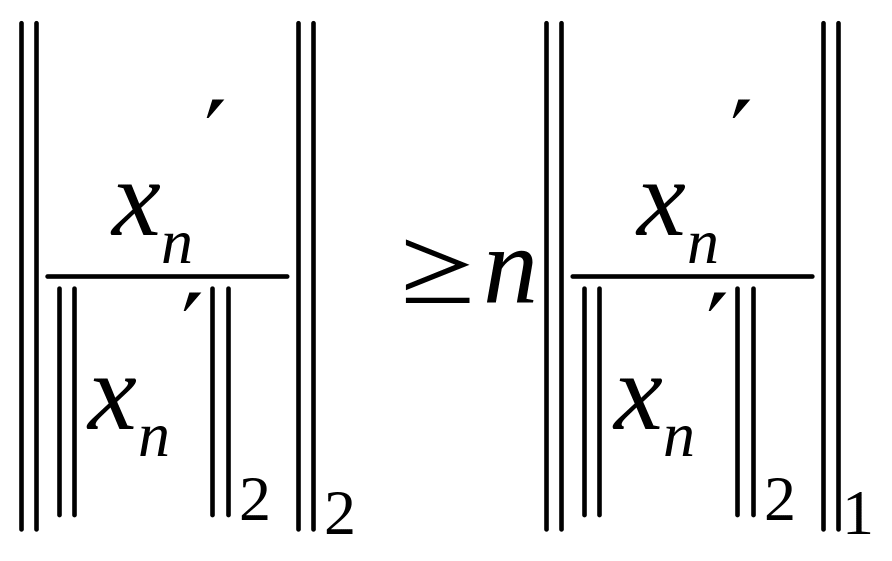
или

, (2.9)

где

,

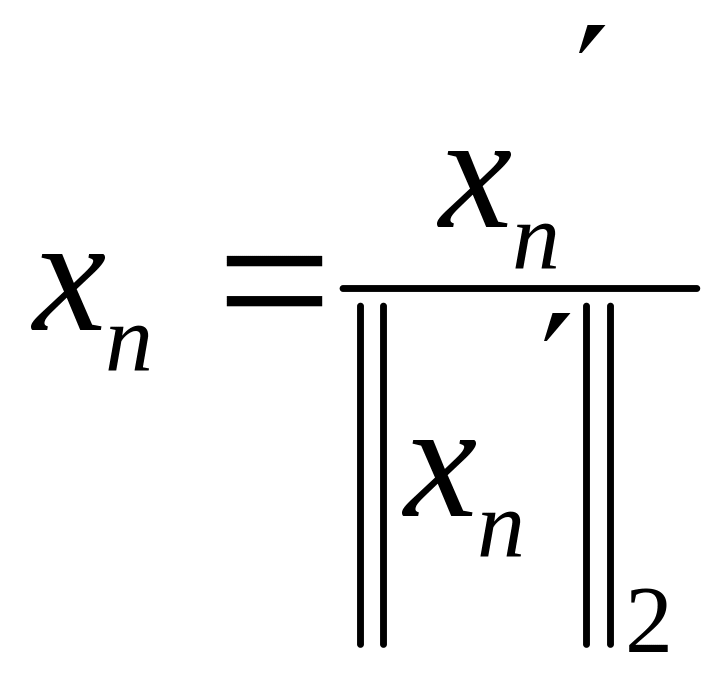причем . С другой стороны из неравенства (2.9) немедленно следует, что

, при .

Таким образом, построили последовательность , которая сходится к нулю по первой норме и не сходится по второй. Это противоречие и доказывает теорему.

Определение 14. Пусть в линейном нормированном пространстве заданы две нормы: и . Нормы и называются эквивалентными, если найдутся такие постоянные и , что

, . (2.10)

Имеет место предложение.

Предложение 14. Две нормы и эквивалентны тогда и только тогда, когда сходимость по одной норме влечет сходимость по другой норме.

Доказательство этого предложения сразу следует из теоремы 1.

В заключение этого параграфа заметим, что отношение эквивалентности норм обладает следующими свойствами:

1. (рефлексивность);

2. Если , то (симметричность);

3. Если и ,то (транзитивность).

Здесь значок означает эквивалентность норм.

2.5. Конечномерные нормированные пространства

Имеет место теорема.

Теорема 2. Во всяком конечномерном линейном пространстве все нормы эквивалентны.

Доказательство. Пусть задано - мерное линейное пространство с базисом . Разложим произвольный элемент этого пространства по базису

и введем норму

.

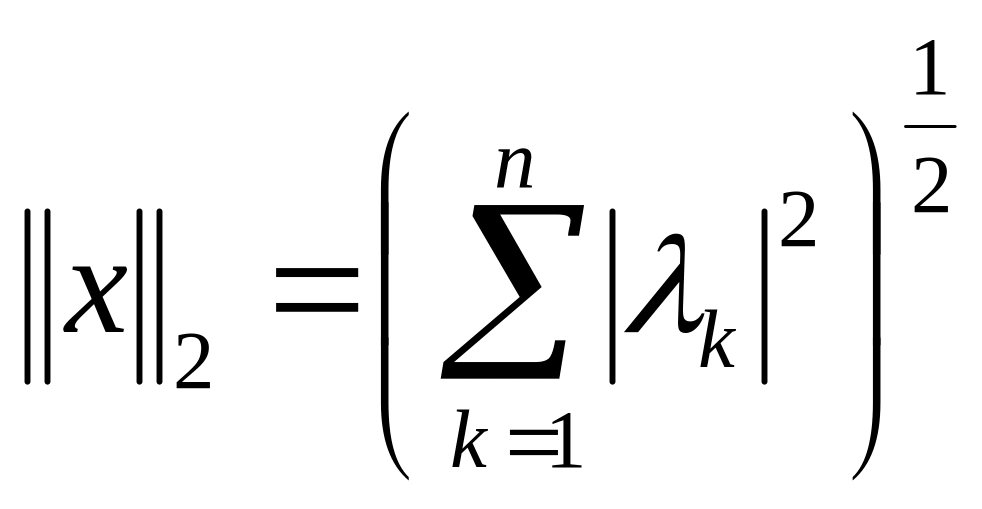С этой нормой пространство можем отождествить с арифметическом пространством упорядоченных наборов из действительных чисел .

Пусть - еще одна произвольная норма в . С помощью неравенства Коши-Буняковского [3] имеем

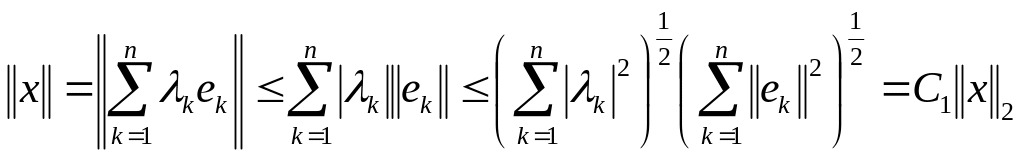. (2.11)

Следовательно, норма подчинена норме . Далее будем доказывать, что норма подчинена норме . С этой целью на поверхности единичного шара пространства рассмотрим функцию

.

Из неравенства

следует, что - непрерывная функция. По теореме Вейерштрасса на ограниченном и замкнутом множестве функция достигает своей нижней грани: найдется такое, что , где нижняя грань берется по всем . Причем , поскольку . Отсюда уже для любого и соответственно для любого имеем

.

Таким образом, подчинена норме . Теорема полностью доказана.

Используя эту теорему, докажем ряд важных предложений.

Предложение 15. Для любого все его координаты удовлетворяют неравенству

, (2.12)

где С – константа, зависящая только от выбора базиса в .

Доказательство. Из теоремы 2 непосредственно выводим

,

где , а

Предложение доказано.

Предложение 16. В конечномерном нормированном пространстве сходимость по норме совпадает со сходимостью по координатам.

Доказательство. Пусть задана последовательность и элемент . Все элементы разложим по базису:

, ,

.

Вначале предположим, что имеется сходимость по координатам, т.е.

.

Используя непрерывность суммы и произведения в нормированных пространствах, получим

, ,

.

И доказана сходимость по норме. Теперь предположим, что имеется сходимость по норме. Применяя неравенство (2.12) к элементам , получим

.

Как следствие этого неравенства: из сходимости по норме следует сходимость по всем координатам. Предложение доказано.

Определение 15. Последовательность называется фундаментальной, если для любого положительного числа найдется такой номер , что для всех верно неравенство .

Нетрудно показать, что любая сходящаяся последовательность фундаментальна. Обратное утверждение, вообще говоря, неверно.

Определение 16. Линейное нормированное пространство называется полным, если каждая фундаментальная последовательность имеет предел.

Предложение 17. Конечномерное нормированное пространство полно.

Доказательство. Возьмем фундаментальную последовательность , . Применяя неравенства (2.12) к разности элементов , получим

.

Тогда, благодаря полноте множества вещественных чисел существуют конечные пределы

, .

И по предложению 16 имеем

.

Предложение доказано.

Определение 17. Замкнутое линейное многообразие в нормированном пространстве называется подпространством.

Предложение 18. Всякое конечномерное линейное многообразие нормированного пространства является подпространством.

Доказательство. Пусть мерно. Возьмем последовательность и допустим, что . Тогда последовательность является фундаментальной в . По предыдущему предложению существует такой , что . Но поскольку во всем пространстве предел сходящейся последовательности – единственный, то , т.е. . Это и означает замкнутость линейного многообразия . Предложение доказано.