Симплекс-таблицi

Спочатку розглянемо допоміжне твердження, що дозволяє стандартним чином (за допомогою симплекс-перетворення) обчислювати симплекс-рiзницi для змінних у КЗЛП.

Нехай на s-у кроцi симплекс-методу є КЗЛП

Лема 1.5. Якщо з цільової функції L(x) КЗЛП виключити базисні змінні, то коефіцієнтами при небазисних змінних будуть відповідні їм симплекс-рiзницi i з'являється вільний член, що дорівнює значенню цільової функції в базисній точці, що розглядається.

Тепер симплекс-рiзницi змінних у КЗЛП легко одержати, якщо на початковій iтерацiї додати до вихідних непрямих обмежень ЗЛП рівняння L(x ) = 0, з якого виключені базисні змінні. На наступних iтерацiях симплексне перетворення застосовується також i до цього нового рівняння.

При проведенні ручних розрахунків, пов'язаних з розв'язуванням ЗЛП симплексним методом, зручно всі обчислення на кожній iтерацiї заносити до симплекс-таблицi, що має такий вигляд:

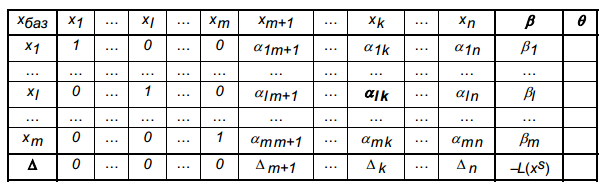
6.

7. Метод штучного базису

:

застосовується в тих випадках, коли для канонічної форми задачі ЛП не означений початковий опорний план. Тоді симплекс-методом розв’язується перетворена задача зі штучним базисом. Вона утворюється з початкової задачі додаванням до лівої частини векторного рівняння-обмеження стількох штучних одиничних векторів з відповідними невід’ємними штучними змінними,  щоб створена матриця містила систему т одиничних, лінійно-незалежних векторів. В цільову функцію початкової задачі додається складова, яка дорівнює добутку суми штучних змінних на число (-М), в разі  максимізації Z, або +М, в разі мінімізації Z, де М - досить велике число.

Якщо в оптимальному плані задачі зі штучним базисом усі штучні змінні дорівнюють нулю, то відповідний опорний план є оптимальним планом початкової задачі. Якщо оптимальний план задачі зі штучним базисом містить хоч одну штучну змінну або задача нерозв’язна, то початкова задача  також не має розв'язків.

У попередніх параграфах розглядався випадок, коли система обмежень задачі лінійного програмування містила одиничну матрицю порядку m. Проте більшість задач не можна звести до потрібного вигляду. В такому разі застосовується метод штучного базису.

Розглянемо задачу лінійного програмування:

 (2.60)

 (2.61)

 (2.62)

Задача подана в канонічному вигляді і система обмежень (2.61) не містить одиничної матриці. Отримати одиничну матрицю можна, якщо до кожного рівняння в системі обмежень задачі додати одну змінну . Такі змінні називають штучними. (Не обов’язково кількість введених штучних змінних має дорівнювати m. Їх необхідно вводити лише в ті рівняння системи обмежень, які не розв’язані відносно базисних змінних.) Допустимо, що система рівнянь (2.61) не містить жодного одиничного вектора, тоді штучну змінну вводять у кожне рівняння:

 (2.63)

У результаті додавання змінних у рівняння системи (2.61) область допустимих розв’язків задачі розширилась. Задачу з системою обмежень (2.63) називають розширеною, або М-задачею

8.

9.

10.11.

Зв’язок міжрозв’язками пари двоїстихзадач.Теорема двоїстості

Розглянемо кілька двоїстих задач, утворену основною задачею лінійного програмування і двоїстої до неї.

Вихідною задачею є: найти максимум функції

 (1)

при умовах

 (2)

 (3)

Двоїста задача: знайти мінімум функції

 (4)

при умовах

 (5)

Кожна з задач двоїстої пари (1) — (3) і (4), (5) фактично є самостійною задачею лінійного програмування і може бути вирішена незалежно одна від іншої. Однак при визначенні симплексним методом оптимального плану однієї з задач тим самим знаходиться рішення й інша задача.

Існуючі залежності між рішеннями прямої і двоїстої задач характеризуються сформульованими нижче лемами і теоремами подвійності.

Лемма 1.1. Якщо X — деякий план вихідної задачі (1) — (3), а В — довільний план двоїстої задачі (4), (5), те значення цільової функції вихідної задачі при плані X завжди не перевершує значення цільової функції двоїстої задачі при плані Y, тобто F(X) F*(Y)

Лемма 1.2. Якщо F(X*) = F*(Y*) для деяких планів X* і Y* задач (1) — (3) і (4), (5), те X* — оптимальний план вихідної задачі, a Y* — оптимальний план двоїстої задачі

Теорема 1. (перша теорема подвійності) Якщо одна з пари двоїстих задач (1) — (3) чи (4), (5) має оптимальний план, те й інша має оптимальний план і значення цільових функцій задач при їхніх оптимальних планах рівні між собою, тобто  .

Якщо ж цільова функція однієї з пари двоїстих задач не обмежена (для вихідної (1) — (3) —зверху, для двоїстої (4), (5) — знизу), то інша задача взагалі не має планів.

Теорема 2. (друга теорема подвійності). План  задачі (1) — (3) і план  задачі (4), (5) є оптимальними планами цих задач тоді і тільки тоді, коли для будь-якого  виконується рівність

Геометрична інтерпретація двоїстих задач. Якщо число перемінних у прямій і двоїстої задачах, що утворять дану пару, дорівнює двом, то, використовуючи геометричну інтерпретацію задачі лінійного програмування, можна легко знайти рішення даної пари задач При цьому має місце один з наступних трьох взаємно виключають один одного випадків: 1) обидві задачі мають плани; 2) плани має тільки одна задача; 3) для кожної задачі двоїстої пари безліч планів порожньо

1. Для задачі, що складає у визначенні максимального значення функції F = 2x1+7x2 при умовах

-

2 x1 + 3x2 14,

x1 + x2  8,

x1, x2 0,

скласти двоїсту задачу і знайти рішення обох задач.

Рішення. Двоїстою задачею стосовно вихідного є задача, що складається у визначенні мінімального значення функції F*=14y1 + 8y2 при умовах

- 2y1 + y2  2

3y1 + y2  7,

y1, y2  0.

Як у вихідної, так і в двоїстій задачі число невідомих дорівнює двом. Отже, їхнє рішення можна знайти, використовуючи геометричну інтерпретацію задачі лінійного програмування (рис. 1. і 2.)

Як видно з мал. 1., максимальне значення цільова функція вихідної задачі приймає в крапці В Отже, Х* = (2; 6) є оптимальним планом, при якому Fmax= 46.

Мінімальне значення цільова функція двоїстої задачі приймає в крапці Е (мал. 4.). Виходить, Y* = (1; 4) є оптимальним планом двоїстої задачі, при якому Fmin=46 Таким чином, значення цільових функцій вихідної і двоїстої задач при їхніх оптимальних планах рівні між собою.

Одночасно, як видно з мал. 2., значення цільової функції двоїстої задачі при будь-якому її плані не менше 46. Таким чином, при будь-якому плані вихідної задачі значення цільової функції не перевершує значення цільової функції двоїстої задачі при її довільному плані.

2. Знайти рішення двоїстої пари задач.

Вихідна задача:

- 4x1 + 2x2  4, 

x1 + x2  6,

x1, x2  0.

Двоїчна задача:

 - 4y1 + y2  -2,

2y1 + y2  -3,

y1, y2  0.

Рішення. Як вихідна, так і двоїста задача містять по двох перемінні. Тому їхнє рішення знаходимо, використовуючи геометричну інтерпретацію задачі лінійного програмування (мал. 3. і 4.). З мал. 3. видно, що вихідна задача не має оптимального плану через необмеженість знизу її цільової функції на безлічі припустимих р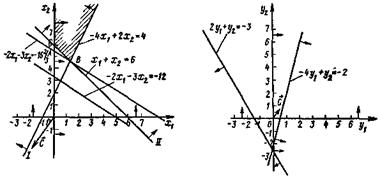 ішень.

З мал. 4. випливає, що двоїста задача не має планів, оскільки багатокутник рішень її порожній. Це означає, що якщо вихідна задача двоїстої пари не має оптимального плану через необмеженість на безлічі припустимих рішень її цільової функції, те двоїста задача також не має планів.

Перебування рішення двоїстих задач. Розглянемо пари двоїстих задач — основну задачу лінійного програмування (1) — (3) і двоїсту до неї задачу (4), (5).

Припустимо, що за допомогою симплексного методу знайдений оптимальний план X* задачі (1) — (3) і цей план визначається базисом, утвореним векторами Рi1, Рi2,…,Pim.

Позначимо через С6=(ci1,ci2,…,cim) вектор-рядок, складений з коефіцієнтів при невідомих у цільовій функції (1) задачі (1) — (3), а через Р-1— матрицю, зворотну матриці Р, складеної з компонентів векторів Рi1, Рi2,...,Рimбазисa. Тоді має місце наступне твердження.

Теорема 3. Якщо основна задача лінійного програмування має оптимальний план X*, тo Y* = С6Р-1 є оптимальним планом двоїстої задачі.

Таким чином, якщо знайти симплексним методом оптимальний план задачі (1) — (3), те, використовуючи останню симплекс-таблицю, можна визначити С6 і Р-1 і за допомогою співвідношення Y*=С6Р-1 знайти оптимальний план двоїстої задачі (4), (5).

У тому випадку, коли серед векторів Р1, P2,…,Рn, складених з коефіцієнтів при невідомих у системі рівнянь (2), мається m одиничних, зазначену матрицю Р-1 утворять числа перших m рядків останньої симплекса-таблиці, що коштують у стовпцях даних векторів Тоді немає необхідності визначати оптимальний план двоїстої задачі множенням C6 на Р-1, оскільки компоненти цього плану збігаються з відповідними елементами (m+1)-й рядка стовпців одиничних векторів, якщо даний коефіцієнт cj=0, і дорівнюють сумі відповідного елемента цього рядка і cj якщо cj  0.

Сказане вище має місце і для симетричної пари двоїстих задач При цьому тому що система обмежень вихідної задачі містить нерівності виду « », те компоненти оптимального плану двоїстої задачі збігаються з відповідними числами (m+1)-й рядка останньої симплекса-таблиці рішення вихідної задачі Зазначені числа коштують у стовпцях векторів, що відповідають додатковим перемінної