6. Моделирование нелинейной системы второго порядка в Simulink.

Имеющаяся передаточная функция звена второго порядка:

Представим ее в виде:

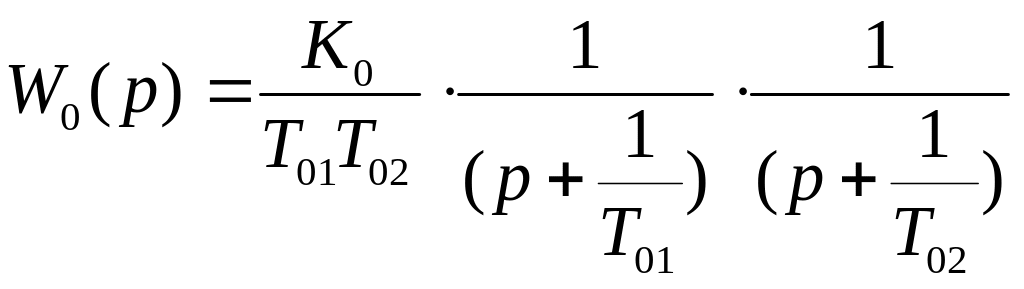
Моделирование системы в Simulink:

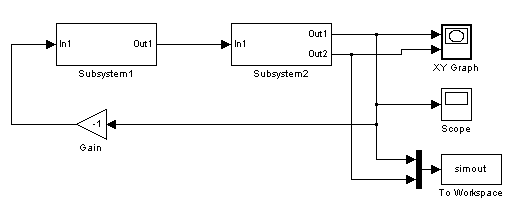
Рис. 3.6.1. Схема модели системы второго порядка

Рис. 3.6.2. Блок Subsystem1

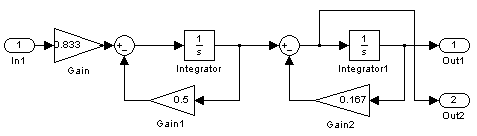
Рис. 3.6.3. Блок Subsystem2

Построим фазовые портреты и переходные пр-сы системы для нач условий: U=1В и U= -1В.

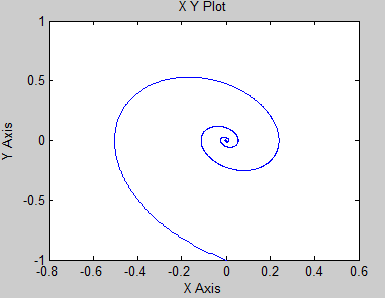
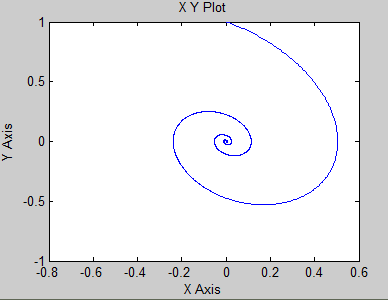
Рис. 3.6.4. Фазовые портреты системы второго порядка при нулевых начальных условиях

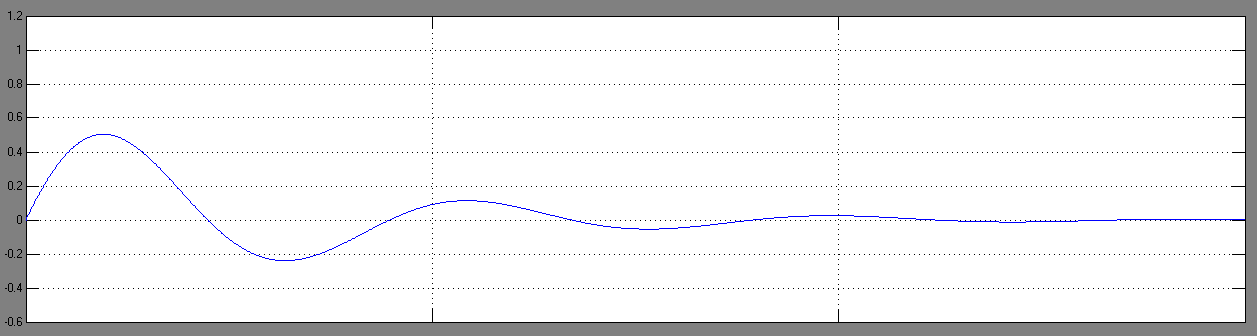
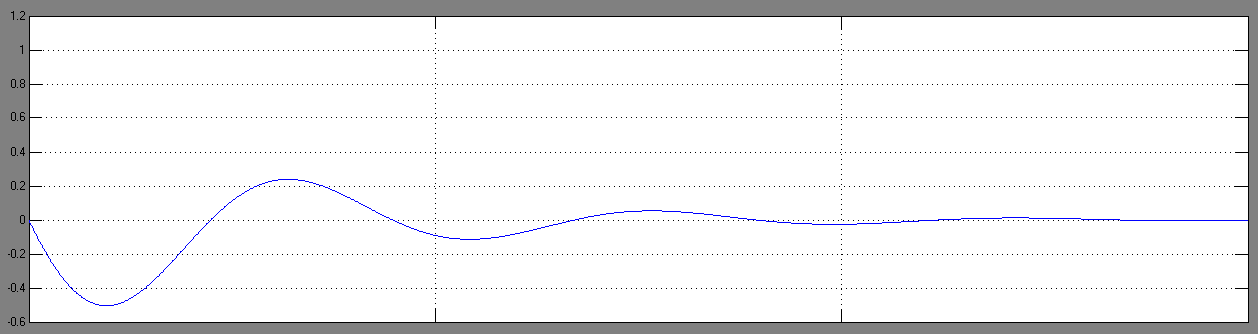
Рис. 3.6.5 Фазовые портреты системы второго порядка при нулевых начальных условиях

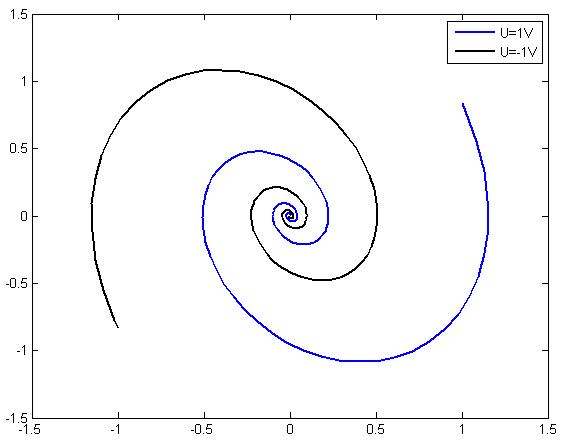
Рис. 3.6.6. Фазовые портреты системы второго порядка при нач условиях: а) U=1B, б) U= -1B

а)

б)

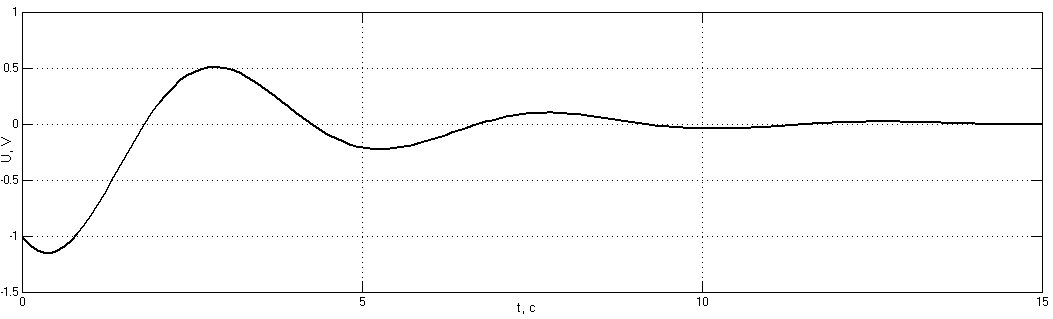
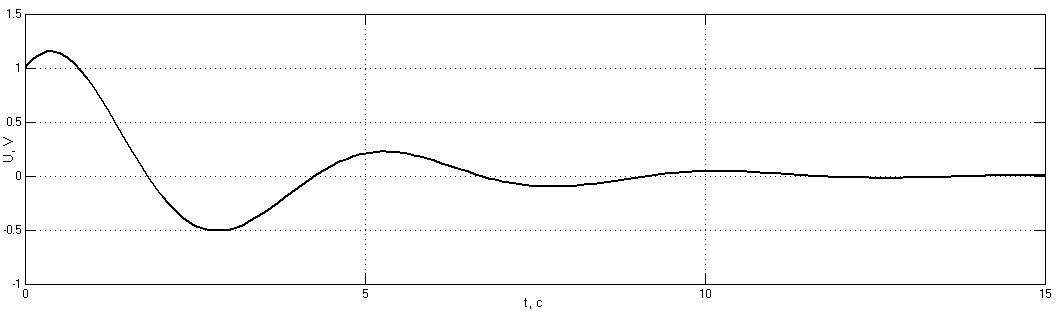
Рис. 3.6.7. Переходные пр-сы в системе второго порядка при нач условиях: а) U=1B, б) U= -1B

Из получившихся графиков видно, что переходные процессы в системе затухают в положении равновесия (U = 0В), вне зависимости от начальных условий, то есть от пути, по которому система попала в это положение.

Введем обратную связь по скорости (К_ос=1) и исследуем ее влияние на процессы в системе.

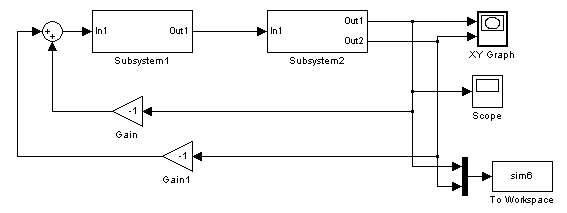
Рис. 3.6.8. Схема модели системы второго порядка с ОС по скорости

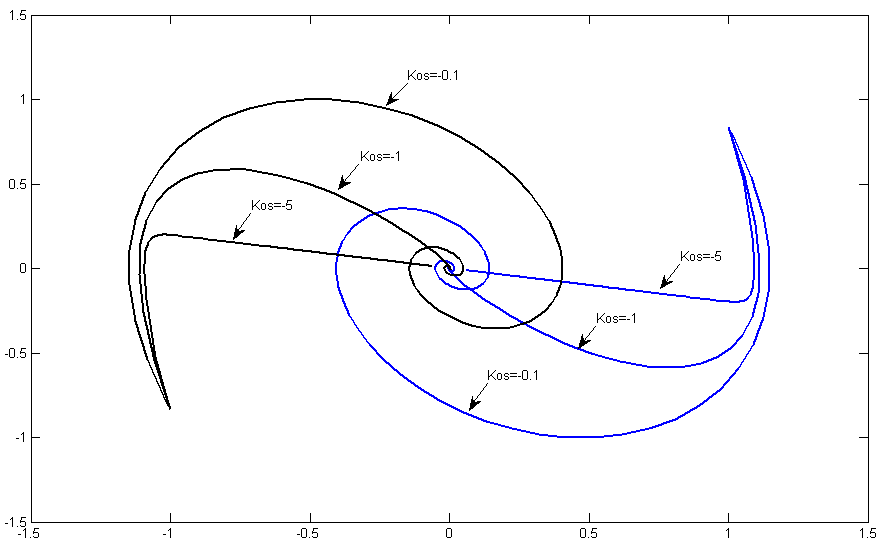
Рис. 3.6.9. Фазовые портреты системы второго порядка с ОС при начальных условиях: а) U=1B, б) U= -1B

а)

б)

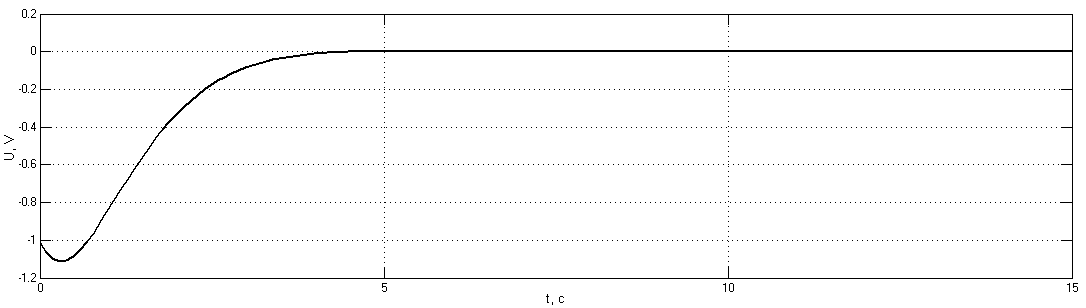
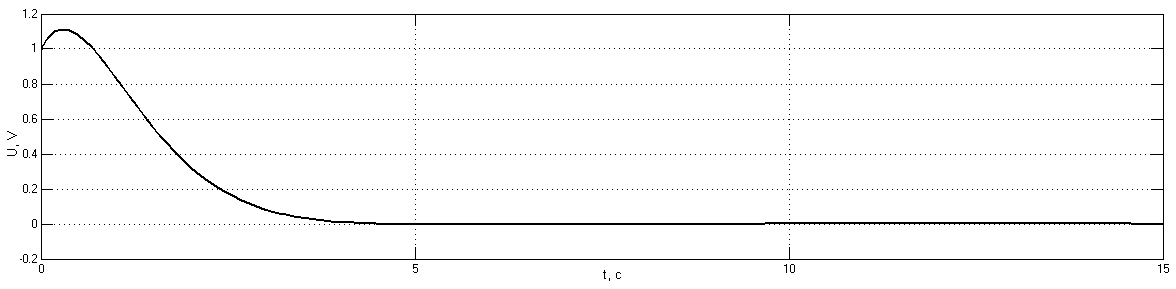
Рис. 3.6.10. Переходные процессы в системе второго порядка с ОС при начальных условиях: а) U=1B, б) U= -1B

Введение обратной связи по скорости приводит исчезновению колебательности в системе. Переходные процессы принимают апериодический характер.

7. Исследование автоколебаний в системе при включении на входе регулятора нелинейного звена

Рис. 3.7.1. Схема модели системы с включенным регулятором нелинейного звена; блоки Subsystem1,2 – те же, что и в схемах на рисунках 3.6.2 и 3.6.3.

Для возбуждения незатухающих автоколебаний данной системе требуется начальное воздействие. При отсутствии начальных условий для любых значений T_p и K_p автоколебания в системе не возникают. При подаче начального воздействия, даже небольшого по амплитуде (U = 0,05 B), в системе возникают незатухающие автоколебания.

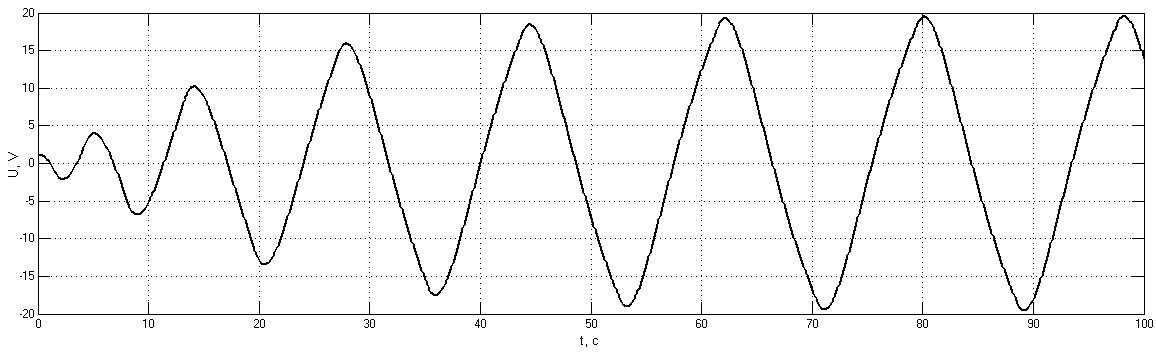
Рис. 3.7.2. Возникновение незатухающих колебаний при небольшом начальном воздействии

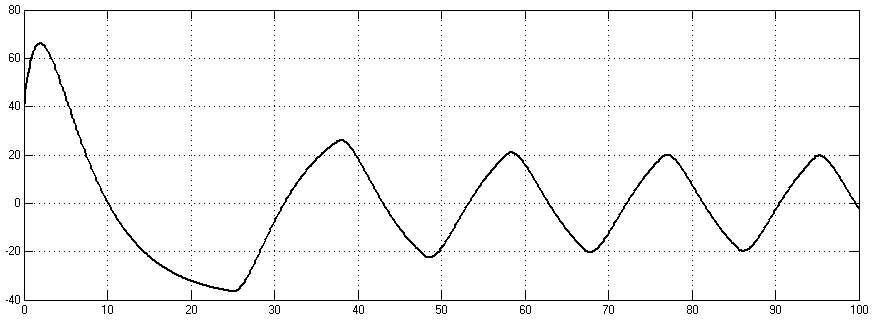
Рис. 3.7.3. Незатухающие колебания при других начальных воздействиях

Из последнего рисунка видим, что автоколебания являются устойчивыми, т.е. при разных входных значениях колебания сходятся к одному и тому же уровню. Граничные значения коэффициента усиления и постоянной времени для инициирования незатухающих колебаний не зависят от подаваемых начальных условий: K_гр=0,03 (min, т.е. при меньших значениях коэффициента усиления колебания затухают), T_гр=1,4 (max, т.е. при больших значениях колебания затухают).

Частота колебаний не зависит от коэффициента усиления регулятора, так как заданная нелинейность однозначна. Получим зависимость амплитуды от коэффициента усиления регулятора.

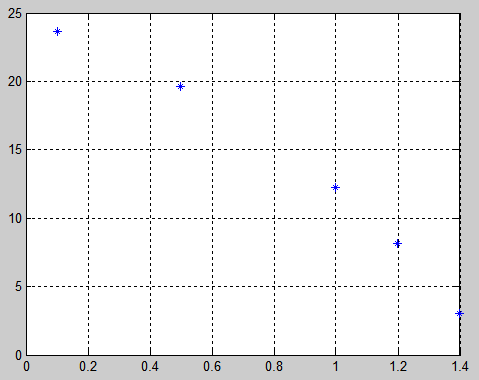
Рис. 3.7.4. Зависимость амплитуды от коэффициента усиления регулятора

а) б)

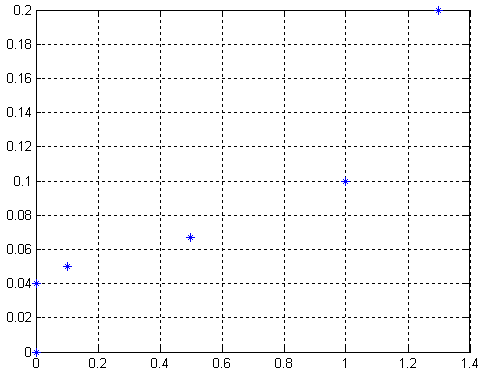
Рис. 3.7.5. Графики зависимости а) амплитуды, б) частоты колебаний от постоянной времени