Санкт-Петербургский Государственный Политехнический Университет

Факультет Технической Кибернетики

Кафедра Компьютерных Систем и Программных Технологий

Курсовой проект

Теория автоматического управления

Работу выполнил

студент группы 4081/10:

Нармания Г.Г.

Преподаватель:

Королев В.С.

Санкт-Петербург

2012г

1. Задание:

1. Исследовать устойчивость разомкнутой и замкнутой системы.

2. Построить границы областей устойчивости в плоскости параметров, отмеченных *.

3. Построить линии равной степени устойчивости в плоскости тех же параметров.

4. Построить переходный процесс для единичного ступенчатого воздействия на входе при нулевых начальных условиях для оптимальных значений параметров (по п.3). Определить показатели качества переходного процесса.

5. Построить фазовый портрет нелинейной системы второго порядка, считая регулятор безынерционным звеном и полагая W_р(p)=1. Сделать выводы о характере процессов в системе. По фазовым траекториям построить примерный вид переходных процессов для характерных начальных условий.

6. Промоделировать нелинейную систему 2-го порядка в Simulink. Сравнить фазовые портреты, полученные расчетным способом с результатами моделирования. Ввести обратную связь по скорости и исследовать ее влияние на процессы в системе.

7. Исследовать автоколебания при включении в систему на входе регулятора нелинейного звена. Исследовать условия возникновения автоколебаний (найти К_гр. или Т_гр.). Построить зависимости амплитуды и частоты автоколебаний от К или Т.

2. Параметры системы:

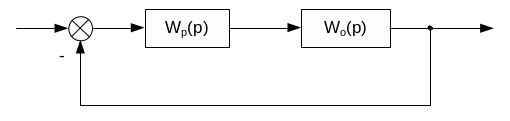
Рис. 2.1. Структурная схема системы

, где K₀ = 100, Т₀₁ = 1 с, Т₀₂ = 4 с

, где K_p= 2, T_p = 0,2 с

Статическая характеристика нелинейности имеет вид:

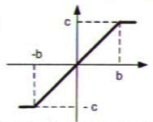
Рис. 2.2. Статическая характеристика нелинейности

Параметры нелинейности: c = 2, b = 1

3. Выполнение работы:

1. Исследование устойчивости разомкнутой и замкнутой системы

ЛАХ и АФЧХ исходной системы:

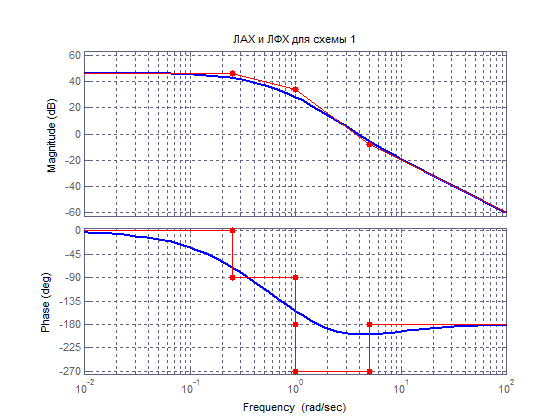
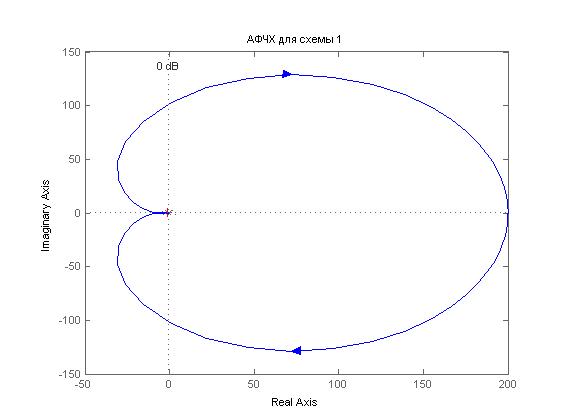
а) Разомкнутая система

Передаточная функция:

Корни характеристического полинома:

Все корни характеристического полинома меньше нуля, сл-но, система устойчивая.

Проверим по критерию Гурвица:

Характеристический полином: 4p³+9p²+6p+1

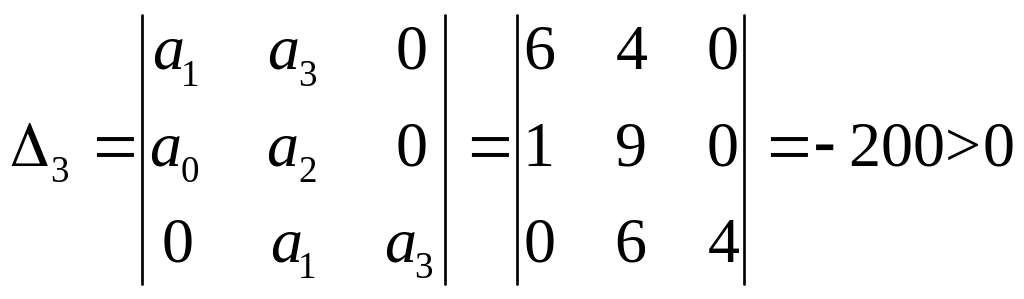
б) Замкнутая система

Передаточная функция:

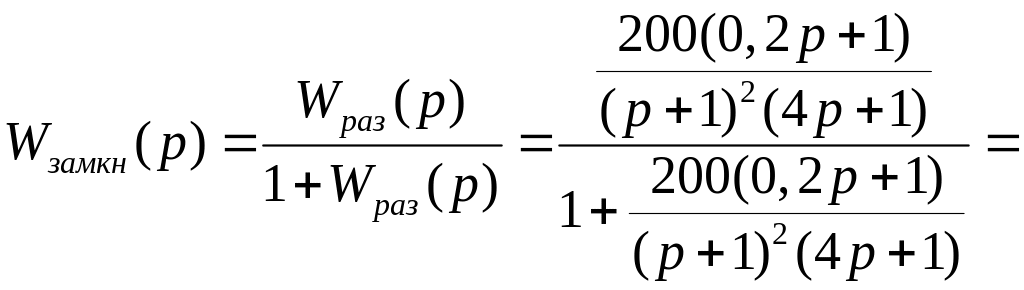
К характеристического полинома:

Проверка по модифицированному критерию Гурвица:

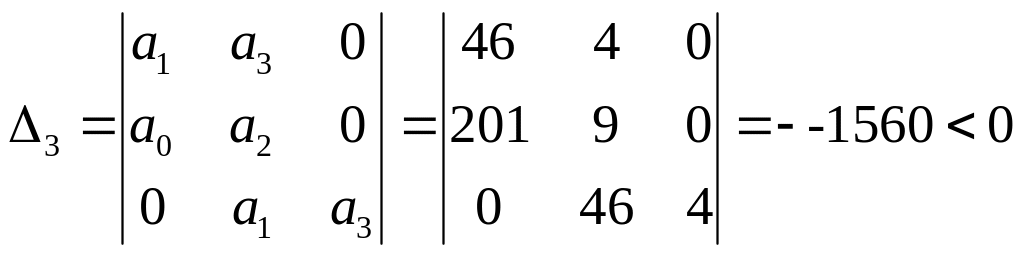,замкнутая система является неустойчивой

С помощью Mаtlab найдем корни характеристического полинома:

>> roots([4 9 46 201])

ans =

0.5396 + 3.8473i

0.5396 - 3.8473i

-3.3293

Система неустойчивая, так как у характеристического полинома есть корни, лежащие в правой полуплоскости.

Проверим критерий Михайлова:

Для разомкнутой системы:

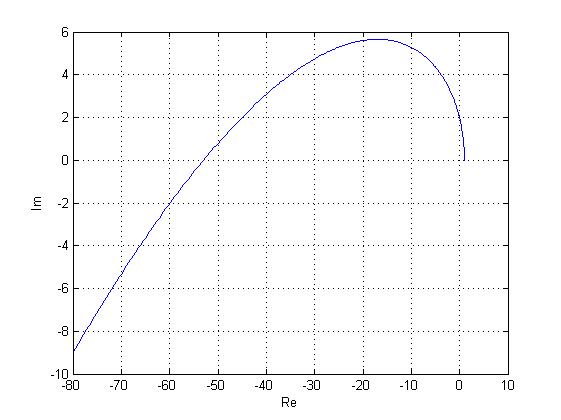
Кривая начинается на положительной полуоси и огибает n=3 квадрантов, соотв-но – система устойчива.

Для замкнутой системы:

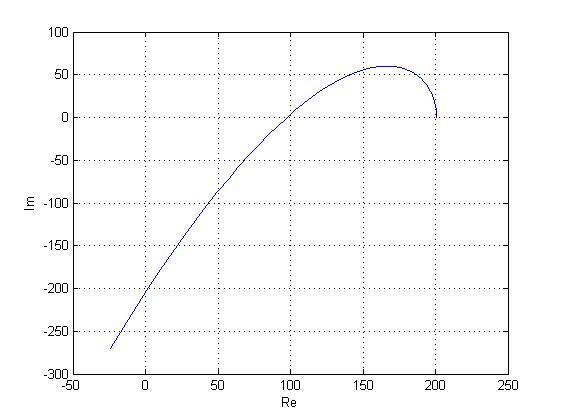
Начинаясь на положительной полуоси кривая не огибает ноль и не проходит 3 квадранта, система не устойчива.

Проверим критерий Найквиста по АФЧХ разомкнутой системы:

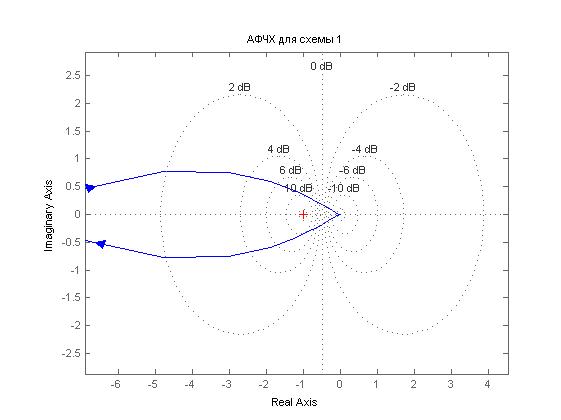
Как видно, кривая огибает точку (-1,0), соответственно замкнутая систем неустойчива.

2. Построение областей устойчивости в плоскости параметров Kp и Tp

Рассчитаем области устойчивости с помощью D-разбиения в плоскости параметров K_p и T_p в программе DCOM пакета Matlab.

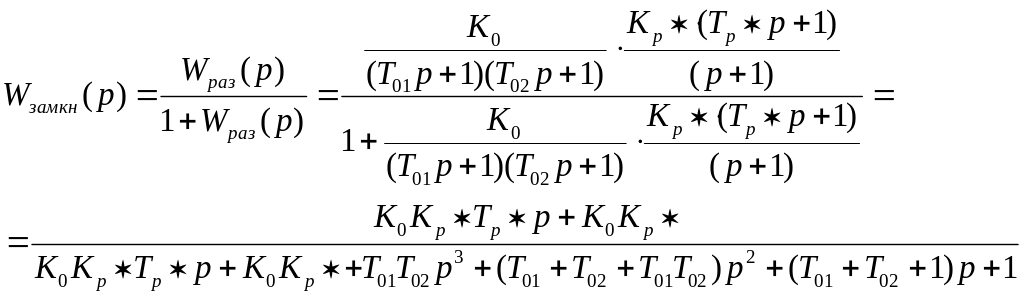
Характеристический полином замкнутой системы:

echo on

>> q = '[4 9 9+100*x*y 1+100*y]';

>> y = [-1:0.01:2];

>> x = [-1:0.01:1];

>> dcom( q, x, y )

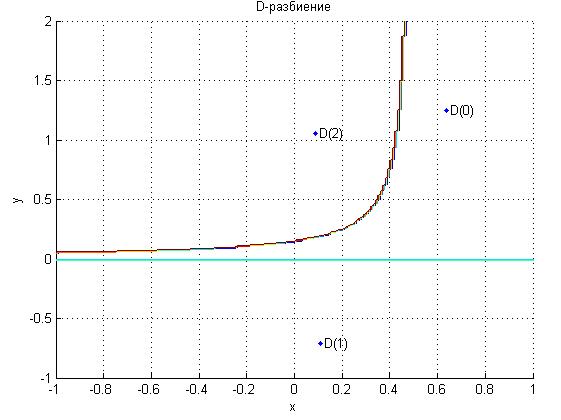
Рис. 3.2.1. Области устойчивости в плоскости параметров K_p и T_p

_{Проверим по критерию Михайлова. Запишем характеристический полином как:}

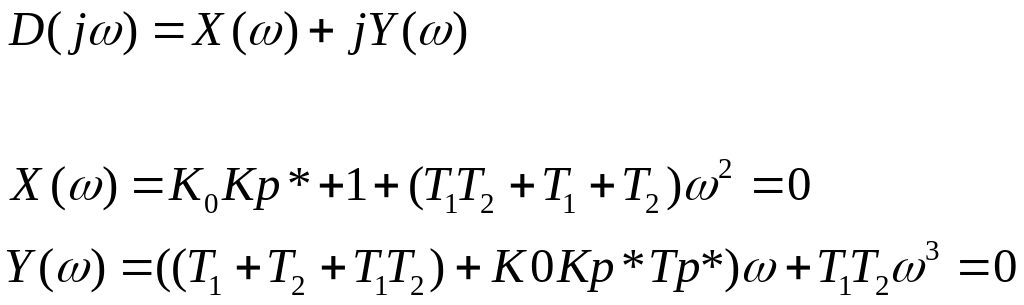
Из второго уравнения получим:

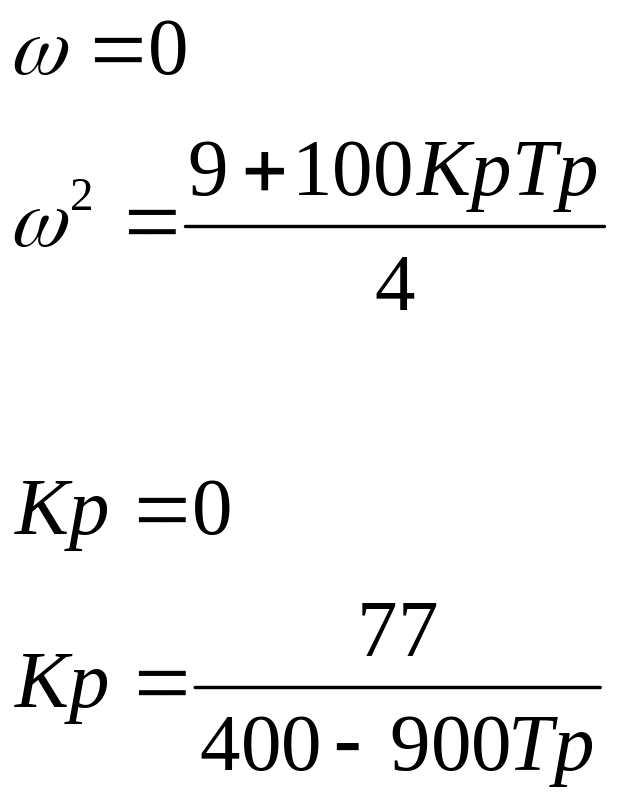
Линии совпадают с полученным посредством DCOM.