9.3. Способы борьбы с гидравлическим ударом

В различных гидравлических системах применяются быстродействующие устройства управления, время срабатывания которых чрезвычайно мало, и величина р_у достигает значительных величин.

Забросы давления могут вывести из строя отдельные агрегаты и трубопроводы. Кроме того, импульсы давления при гидравлическом ударе, распространяющиеся по системе, могут быть причиной неожиданных срабатываний отдельных устройств. Поэтому приходится применять различные способы борьбы с этим явлением.

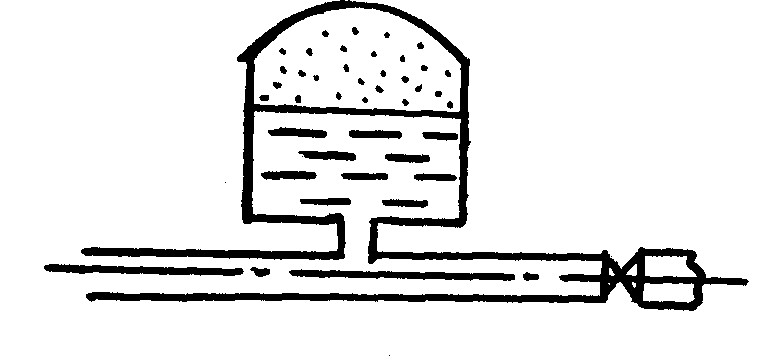
Наиболее эффективным методом борьбы с гидравлическим ударом является устранение возможности прямого гидравлического удара путём применения медленно закрывающихся запорных устройств. Можно применять гидравлические аккумуляторы. Это цилиндрическая ёмкость, которая частично заполнена жидкостью, а частично воздухом. Энергия гидравлического удара расходуется на сжатие воздуха, предохраняя тем самым трубопровод и запорное устройство от разрушения.

Наконец, в ряде случаев применяют специальные противоударные клапаны, которые срабатывают при повышении давления и сбрасывают часть жидкости, что позволяет снизить давление.

Рис. 9.5

Глава 10. Взаимодействие струи с преградой

10.1. Приложение теоремы Эйлера к случаю взаимодействия струи с преградой

Рассмотрим неподвижный криволинейный канал, по которому движется жидкость. Будем полагать движение жидкости установившимся. Выделим два сечения 1-1 и 2-2 (рис. 10.1).

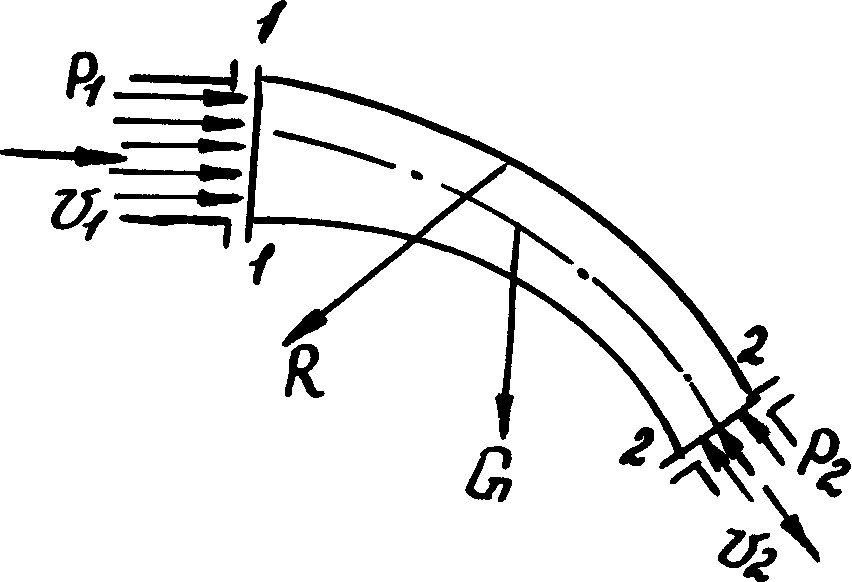
Рис. 10.1

На жидкость действуют следующие силы:

р₁ – сила давления в сечении 1-1;

р₂ – сила давления в сечении 2-2;

G – вес жидкости;

R – сила, с которой стенки канала действуют на жидкость.

Результирующая внешних сил, действующих на жидкость

.

(10.1)

Применим к указанной системе материальных точек и действующим на неё силам теорему Эйлера: производная по времени вектора количества движения системы материальных точек равняется главному вектору внешних сил, действующих на систему:

.

(10.2)

Так как сила R, с которой стенка действует на жидкость, равна силе N, с которой жидкость действует на стенку, и направлена в обратную сторону , получим:

.

(10.3)

Обозначим – статическая составляющая реакции потока, – динамическая составляющая реакции потока

.

(10.4)

10.2. Определение силы давления жидкости на преграду

Рассмотрим силу давления жидкости на стенку конической формы (рис. 10.2).

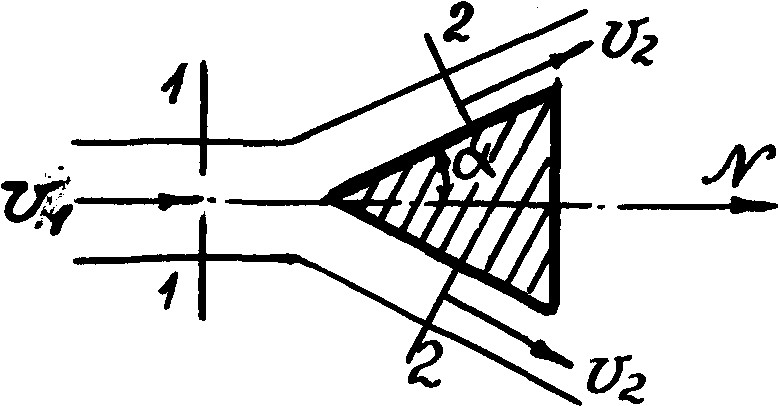
Рис. 10.2

Выделим сечениями 1-1 и 2-2 участок потока. Так как в сечениях 1-1 и 2-2 действует атмосферное давление, то Р₁ = Р₂ = 0.

Если пренебречь весом жидкости G, то статическая составляющая потока будет равна нулю и

.

(10.5)

Если для сечений 1-1 и 2-2 написать уравнение Бернулли, то с учётом указанных выше соображений и упрощений придем к выводу, что v₁ = v₂ = v. Так как поток направлен по оси конической стенки, то сила действия потока на стенку так же направлена по оси.

Спроектируем на это направление векторы сил:

.

(10.6)

Рассмотрим некоторые частные случаи:

1. Струя натекает на плоскую стенку под углом  = 90° (рис.10.3). Тогда используя (10.6), получим:

.

(10.7)

Рис. 10.3

2. Струя натекает на стенку чашеобразной формы, поворачиваясь при этом на 180° (рис.10.4). В этом случае

.

(10.8)

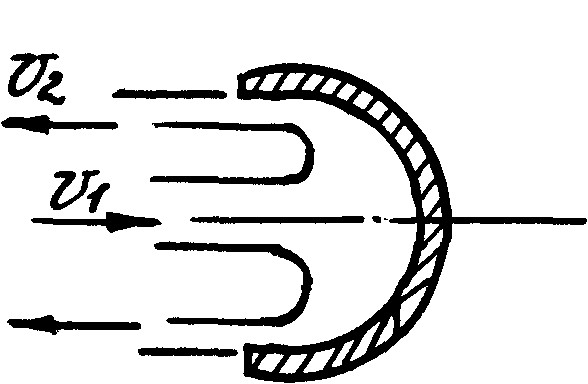
Рис. 10.4

3. Рассмотрим случай натекания жидкости на плоскую стенку, расположенную под углом  к оси струи (рис, 10.5). Пусть жидкость растекается по стенке только двумя потоками (т.е. считаем, что стенка имеет форму желоба). Сила N действия струи на стенку направлена перпендикулярно стенке. Силы Р₁, Р₂, Р₃, равны нулю, а весом жидкости пренебрегаем. Тогда N_ст = 0 следовательно

.

(10.9)

Спроектируем векторы сил на направления х и у (рис. 10.5), получим

	,	(10.10)
	.	(10.11)

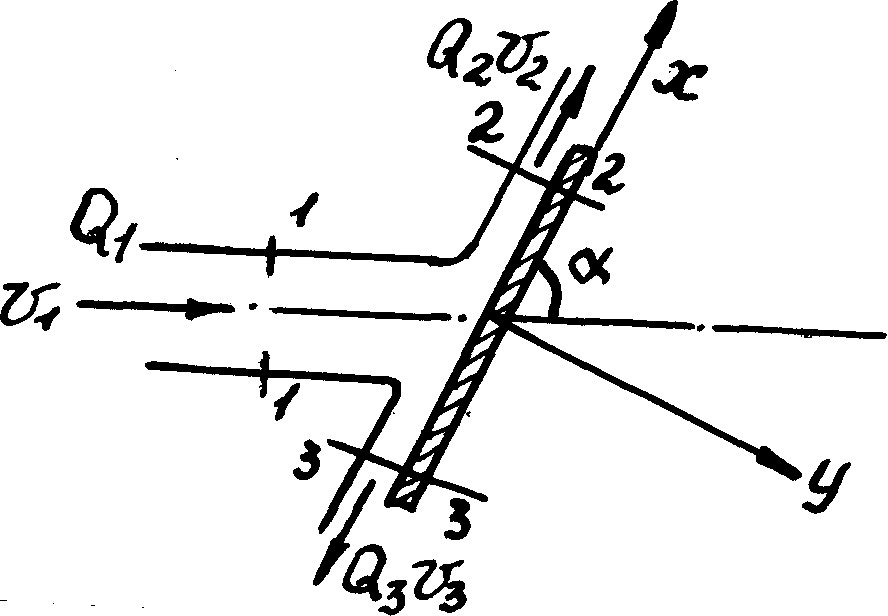
Рис. 10.5

Если пренебречь гидравлическими сопротивлениями на участках 1-1, 2-2, 3-3, то скорости будут одинаковыми и из (10.10) получим:

.

(10.12)

Воспользовавшись очевидным соотношением

.

(10.13)

Из (10.12) и (10.13) легко получить значения расходов Q₂ и Q₃.

64