9.2. Определение величины ударного повышения давления. Основы теории н. Е. Жуковского

Пусть при мгновенном закрытии задвижки волна повышенного давления пройдёт путь l = c t. Если до удара скорость жидкости равнялась v₀, то к концу промежутка времени t она будет v₀ – v (рис.9.3).

Рис. 9.3

Применим к указанному объёму жидкости теорему о количестве движения. В соответствии с этой теоремой

,

(9.1)

или

,

Подставим в левую часть уравнения l = c t, тогда

,

(9.2)

следовательно

.

(9.3)

Переходя к дифференциальной форме, получим

.

Берём интеграл – левую часть в пределах от р₀ до р_у –, а правую от v₀ до v:

.

(9.4)

Интегрируя, получим

.

(9.5)

Обозначим р_у – р₀ = р_у, тогда

.

(9.6)

При мгновенном закрытии задвижки v = 0 и повышение давления будет макси-мальным

.

(9.7)

Для определения скорости распространения ударной волны рассмотрим изменение массы жидкости за промежуток времени t.

До деформации участка трубы длиной l масса жидкости составляет Fl. После гидравлического удара плотность будет ( + ), а площадь (F + F).

Изменение массы жидкости составит

.

(9.8)

Это изменение массы жидкости будет равно массе, притекающей в объём вздутия

.

(9.9)

Следовательно, приравнивая (9.8) и (9.9), получим:

.

(9.10)

По закону Гука

,

(9.11)

где Е_ж – модуль упругости жидкости.

Относительное изменение площади представим следующим образом

,

(9.12)

Пренебрегая весьма малой величиной d², получим:

.

(9.13)

Величина представляет собой относительное увеличение диаметра трубы, которое по закону Гука равно

,

(9.14)

где Е – модуль упругости материала стенки;

– увеличение растягивающего напряжения в стенке трубы.

Рассмотрим чему равно . Для этого изобразим участок рассматриваемой трубы (рис. 9.4).

Рис. 9.4

.

(9.15)

В знаменателе показана площадь, по которой происходит разрыв, а в числителе сила, разрывающая трубопровод. Тогда

,

(9.16)

а

.

(9.17)

Внесём (9.11) и (9.17) в (9.10) и получим:

.

(9.18)

Подставив р_ym=cv₀ и сократив v₀, получим

,

(9.19)

откуда

.

(9.20)

Выражение является скоростью распространения звука или упругих деформаций в жидкой среде и для воды равно 1425 м/с. Следовательно

.

(9.21)

Формулы Н.Е.Жуковского справедливы при очень быстром закрытии задвижки или, когда

.

П ри этом условии имеет место прямой гидравлический удар. При t_зак > t₀ возникает непрямой удар, при котором ударная волна, отразившись от резервуара, возвращается к задвижке раньше, чем она будет полностью закрыта. Повышение давления при этом будет меньше, чем при прямом ударе. При непрямом ударе повышение давления приближённо определяется по формуле:

.

(9.22)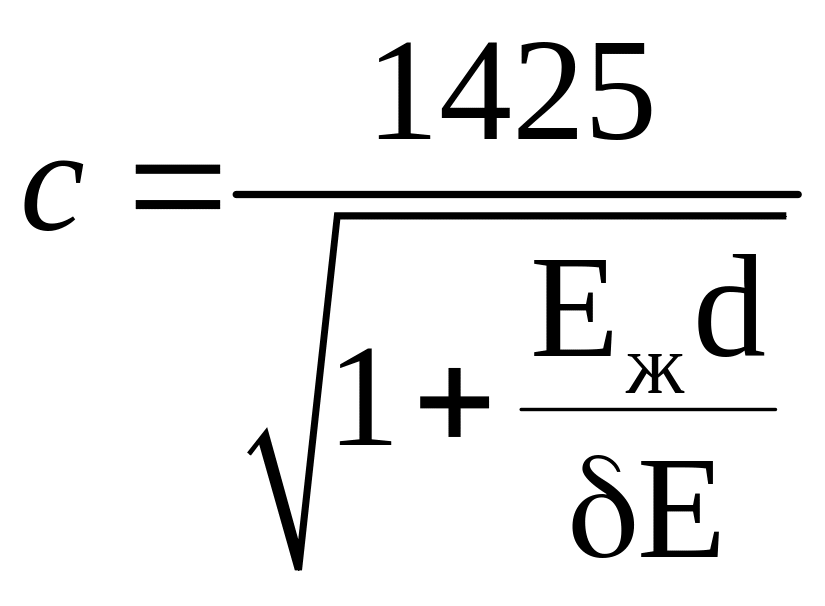