
Шпоры по дискре (3 семестр)
.doc
|
22. (1 из 3) Свойства графа линейного преобразования, заданного с помощью нильпотентной матрицы |
22. (2 из 3) Свойства графа линейного преобразования, заданного с помощью нильпотентной матрицы |
|
Утверждение:
Пусть
A:LpLp
, тогда
М – матрица линейного оператора: М= ◄
Рассмотрим N2(A)= Преобразуем
N2(A):
p1=…=ps=x;
ps+1,…,pk
– отличны от x. Получим: N2(A)= Рассмотрим
|А1|= Заметим, что |S(p)|0, где р(х)х. Действительно: (S(p))=|Е-S(p)|=p, но |S(p)|=p(0) (p(0) – является условной записью свободного коэффициента многочлена p), но так как р(х)х, то р(0)0 |A1|0. |
Рассмотрим
А0= S(xk)k=0 A0 – нильпотентна.► Утверждение: (свойство) Пусть А0 LpLp, |Р|<∞,А0 – нильпотентная. Тогда G(A0) – дерево. ◄Т.к.
А0=
Утверждение:
Пусть А= а)
б)
r |
|
22. (3 из 3) Свойства графа линейного преобразования, заданного с помощью нильпотентной матрицы |
23. (1 из 2)Построение графа линейного преобразования, заданного с помощью нильпотентной матрицы |
|
Рассмотрим
граф
1) С(А) G(A1) 2)
eC(A),
◄без доказательства►
|
Утверждение:
Пусть А0:LpLp
и
rN
т.ч.
1) L – число слоев (уровней) дерева G(A0) 2) Ni – число вершин слоя i, i=1…L 3)
Ki
– число концевых вершин слоя i,
i=1…L
(концевые – в них не входят ребра, но
из них могут выходить
4) R(v) – число ребер, входящих в вершину v. Утверждение: Пусть A0=S(k), тогда: 1) L=k 2) N0=1; N0+…+Ni=qi, i=1…L 3) ki=0, ik 4) R(v)={0,q} ◄
|
|
23. (1 из 2)Построение графа линейного преобразования, заданного с помощью нильпотентной матрицы |
24. (1 из 1)Свойства графа линейного преобразования, заданного с помощью обратимой матрицы |
|
Найдем
число вершин графа G(A0),
из которых корень дерева достижим за
не более чем I
шагов. Легко видеть, что эти вершины
имеют вид
Покажем,
что R(v){0,v}.
Рассмотрим вершину
1) если S10, то R(v)=0 2)
если S1=0,
то
|
Утверждение:
(свойство) Пусть
◄Пусть
Так как
|
|
25. (1 из 2) Цикловые термы. Сведение задачи построения графа линейного преобразования, заданного со помощью обратимой матрицы, к задаче построения линейного преобразования, заданного с помощью сопровождающей матрицы степени неприводимого многочлена. |
25. (2 из 2) Цикловые термы. Сведение задачи построения графа линейного преобразования, заданного со помощью обратимой матрицы, к задаче построения линейного преобразования, заданного с помощью сопровождающей матрицы степени неприводимого многочлена. |
|
Теорема:
Пусть А0:LpLp,
|P|=q,
A0 Положим m1 – число элементов последовательности 1…k, равных 1, m2 – равных 2 и т.д. до mk – число элементов данной последовательности, равных L (например последовательность 2,3,3,5, тогда m1=0,m2=1, m3=2, m4=0, m5=1). Тогда G(A0) определяется следующими параметрами: 1) L=max(1…k) 2)
R(v){0, 3)
N0=1,
N0+…+NL= 4)
Ki=Ni- ◄Доказать самим► Определение:
Пусть
Цикловой
структурой преобразований
Определение:
Пусть
|
Определим
произведение
а) Сумма цикловых термов.
б) Произведение цикловых термов
в)
Утверждение:
Пусть матрица
◄Без доказательства► //Для
матрицы вида
|
|
26. Построение графа линейного преобразования, заданного с помощью сопровождающей матрицы степени неприводимого многочлена (без доказательства) |
26. Построение графа линейного преобразования, заданного с помощью сопровождающей матрицы степени неприводимого многочлена (без доказательства) |
|
Теорема:
Пусть
Тогда
◄Без доказательства► Алгоритм построения графа линейного преобразования
1)
2) Для
|
3)
Для
4)Пусть
5)
К каждой вершине
|

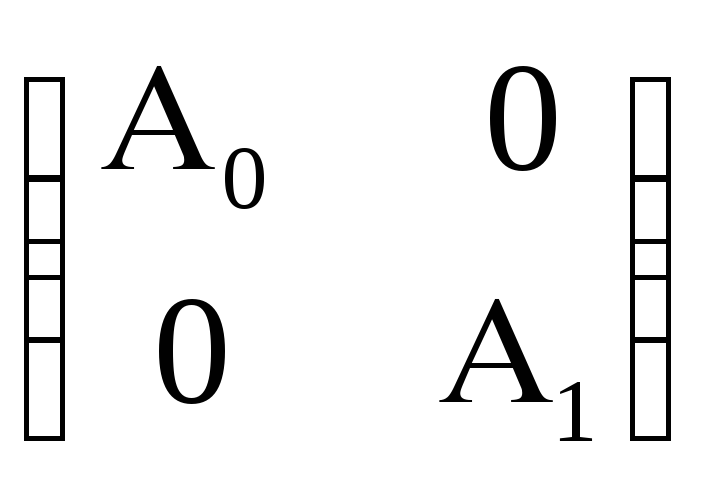 ,
где А0
– нильпотентная матрица (т.е.
rN:
,
где А0
– нильпотентная матрица (т.е.
rN:
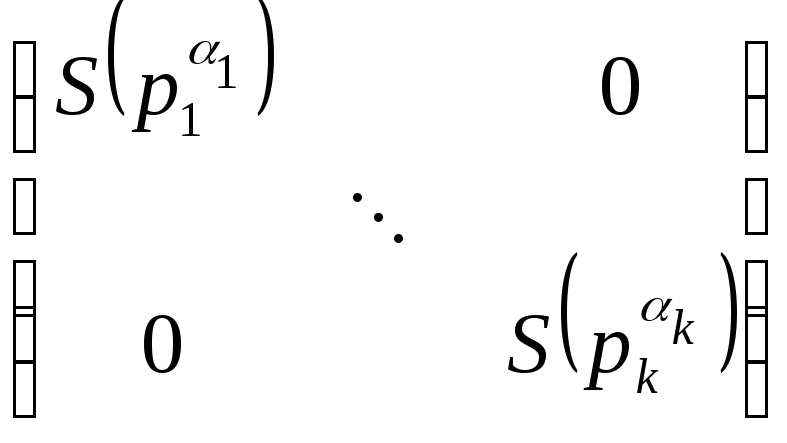 ,
pi
– неприводимые многочлены из P[x].
,
pi
– неприводимые многочлены из P[x].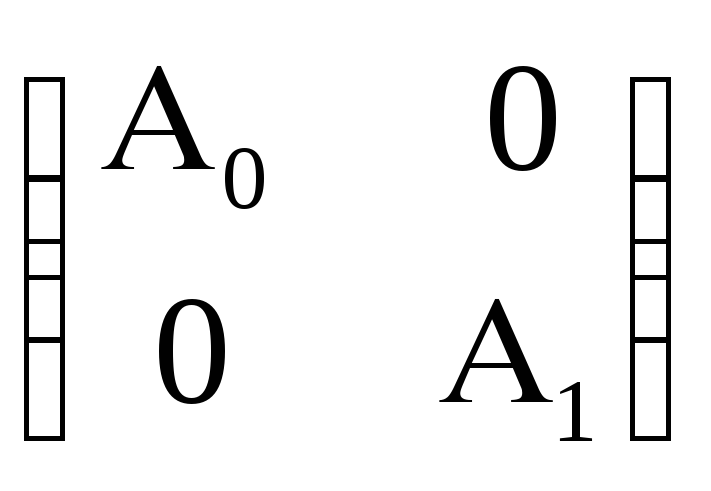 ,
где А0=
,
где А0=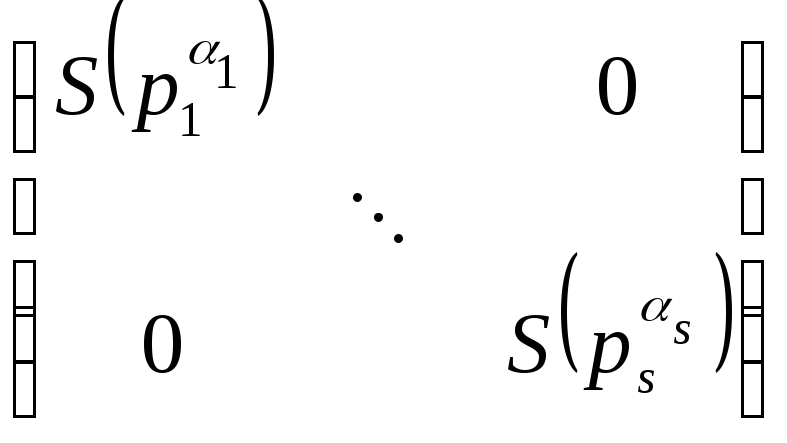 и А1=
и А1=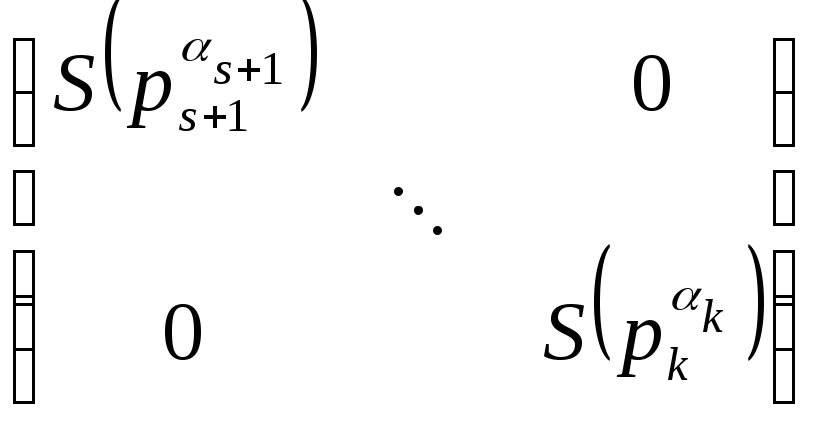 .
.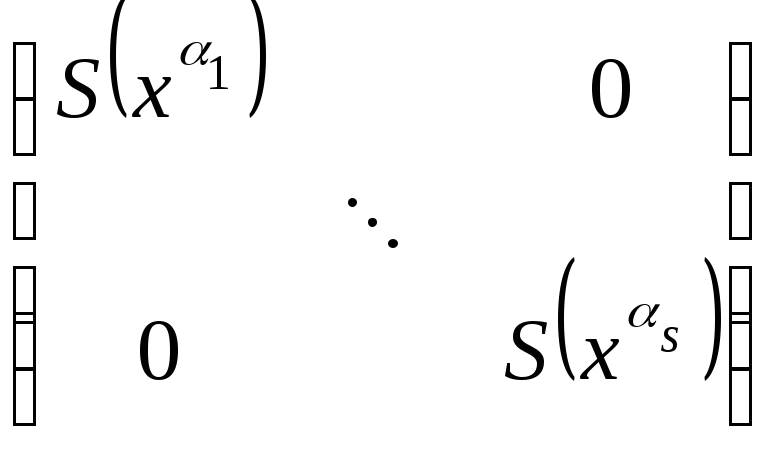 ,
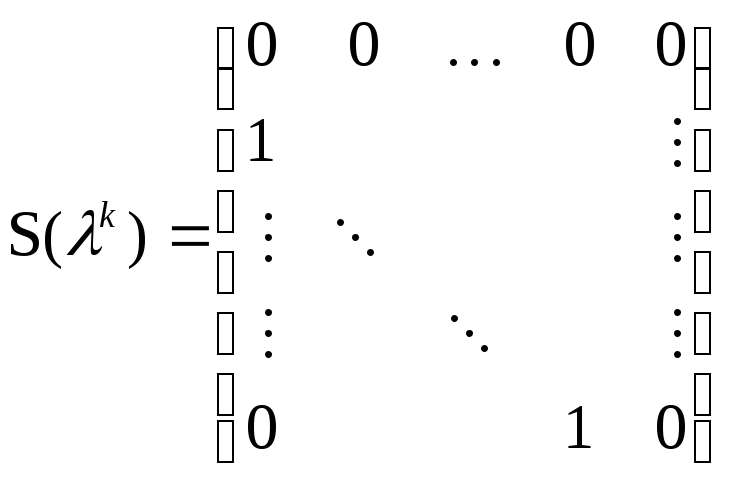
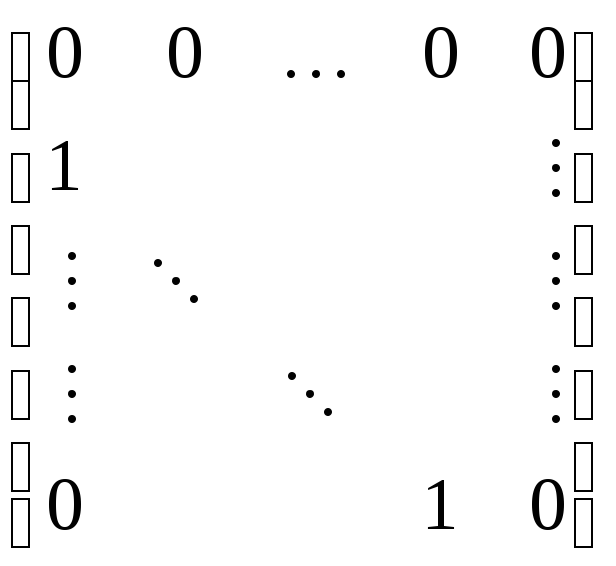
но S(xk)=
,
но S(xk)=
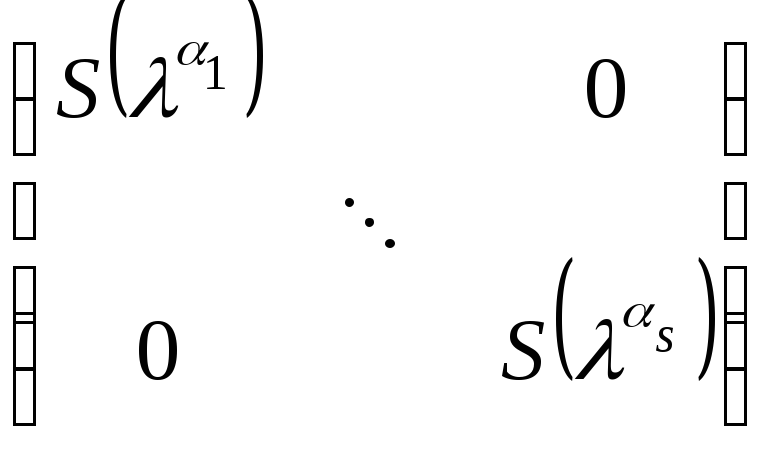 ,
то Утв достаточно доказать для случая
А0=S().
,
то Утв достаточно доказать для случая
А0=S().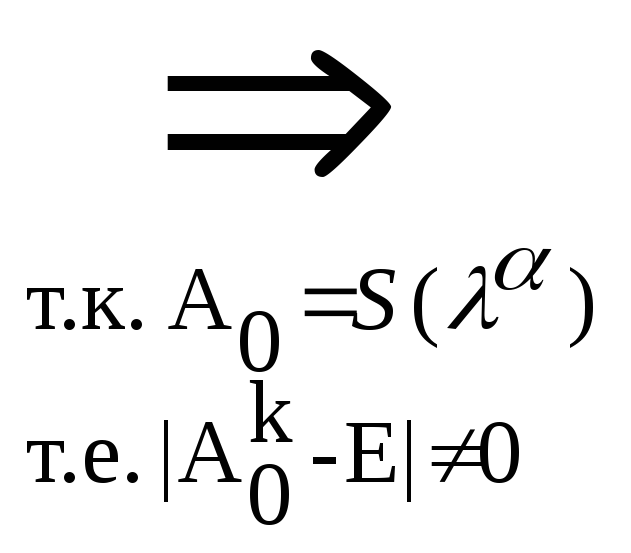 u=0
u=0
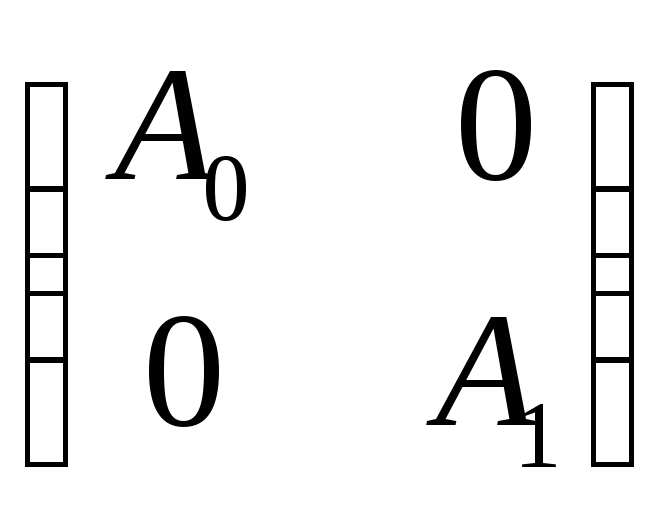 ,
А0
– нильпотентная матрица, А1
– обратимая матрица. Пусть С(А) –
подграф графа G(A),
состоящий из всех вершин графа G(A),
принадлежащих какому либо циклу.
еVC(A)
рассмотрим подграф графа G(A)
– De(A)
вида:
,
А0
– нильпотентная матрица, А1
– обратимая матрица. Пусть С(А) –
подграф графа G(A),
состоящий из всех вершин графа G(A),
принадлежащих какому либо циклу.
еVC(A)
рассмотрим подграф графа G(A)
– De(A)
вида:
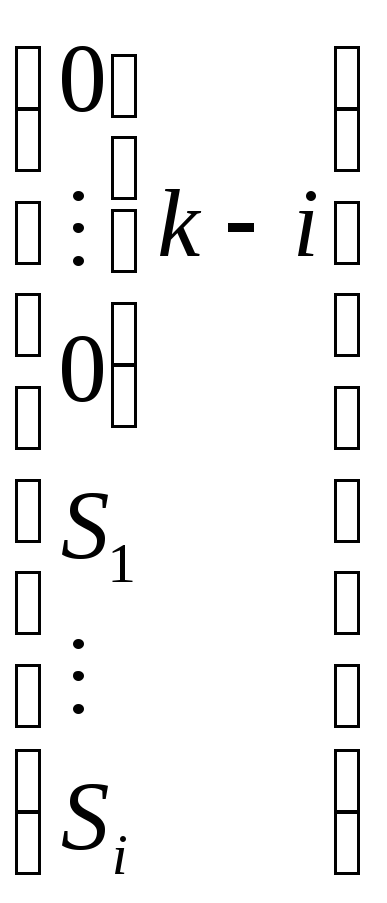 .
Таких векторов qi.
.
Таких векторов qi.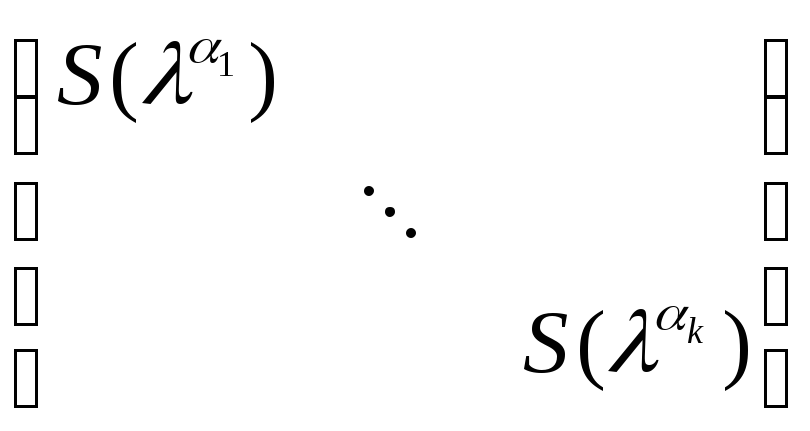 ,
11…kL
,
11…kL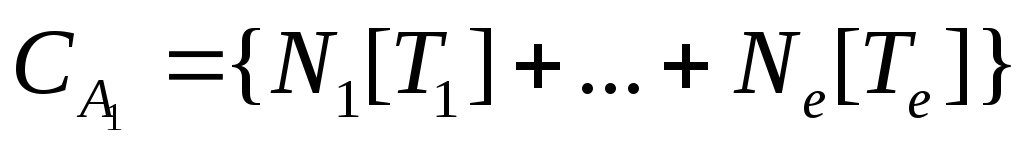 ,
где
,
где
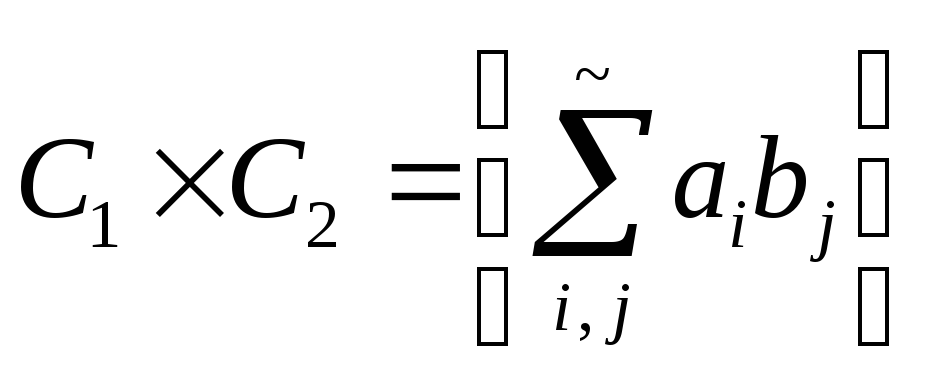 ,
где
,
где
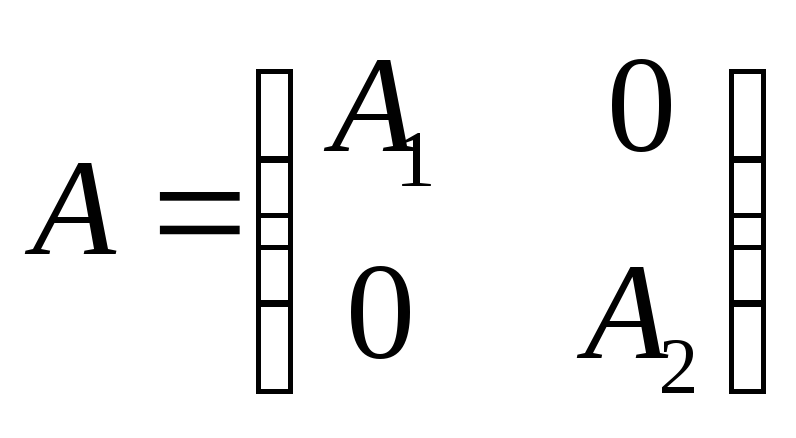 ;
;
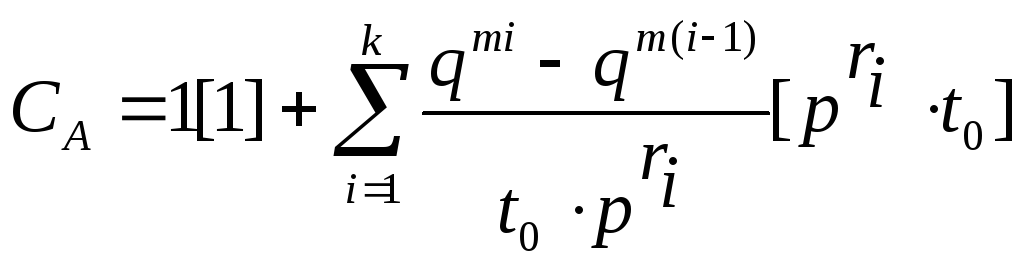 ,
где
,
где
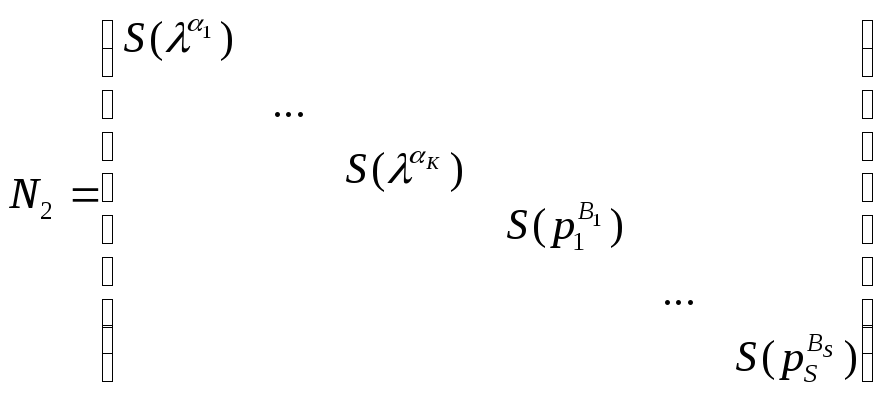
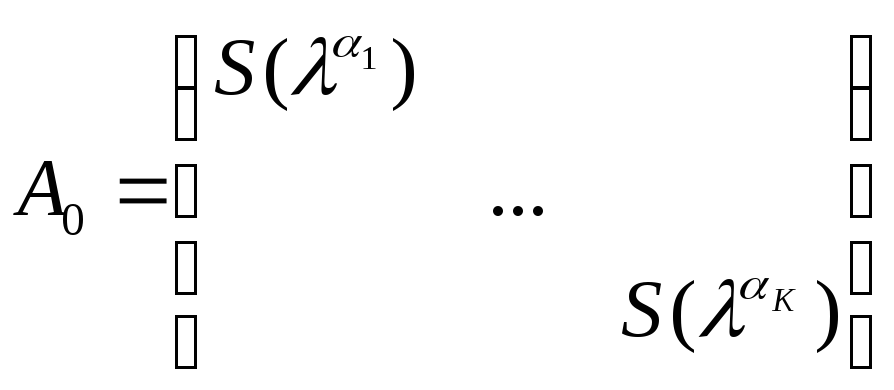 построим
построим
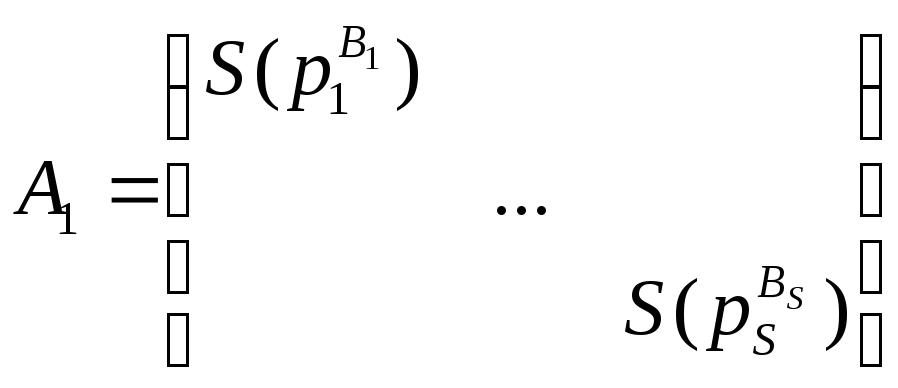 =>
=>