
Шпоры по дискре (3 семестр)
.doc
|
16. (1 из 1) Подобие матриц над полем. Критерий подобия матриц над полем |
17. (1 из 3) Сопровождающая матрица многочлена над полем и ее свойства |
|
Определение:
Теорема:
(критерий)
Пусть
◄без доказательства► Следствие:
|
Определение: Пусть :LpLp – линейное преобразование, заданное с помощью матрицы А. Пусть А()={q()Р[] | q()()=0, Lp}. Множество А() называется множеством аннулирующих многочленов линейного преобразования . q()=Ckk+Ck-1k-1+…+C0E, где q()=Ckk+C0 В матричной форме: q(A)()=0 Lp. Утверждение: А() – идеал кольца Р[], Р[] – кольцо главных идеалов ◄а) если f1,f2A(), то (f1-f2)A() б) gР[] и fA() g*fA() Проверим: g()*f()=(g*f)() (g()=Q, f()=F) Q*F=F*Q (g*f)()()=(g()*f())()=(g())(f()())=g()(0)=0 g*fA()► Сл А()=<m()>, m()Р[]. Определение: Унитарный многочлен m(x) аннулирующий преобразование и имеющий минимальную степень называется минимальным многочленом преобразования . Если задано с помощью матрицы А, то m() или mA() – минимальный многочлен матрицы А. Утверждение:
А – матрица над полем Р. mA()= (()=|E-A|)
Если в условии утверждения k(E-A)=Diag(1,…1,f,…,fk), то mA()=fk. ◄()=f1…fk
|
|
17. (2 из 3) Сопровождающая матрица многочлена над полем и ее свойства |
17. (3 из 3) Сопровождающая матрица многочлена над полем и ее свойства |
|
Определение:
Матрица S(f)= Утверждение:
K(E-S(f))= ◄E-S(f)= Найдем
|
=
|
|
18. (1 из 2) Существование и единственность представления матрицы над полем в 1-ой нормальной форме |
18. (2 из 2) Существование и единственность представления матрицы над полем в 1-ой нормальной форме |
|
Определение:
Теорема: А-матрицы размером nxn над полем Р ! N1(A) – матрица в первой нормальной форме: АN1(A). ◄Пусть
К(E-A)=Diag Заметим,
что ft()0
(если бы ft()=0,
то характеристический многочлен был
бы равен 0, а это невозможно в силу
определения характерестического
многочлена или |k(E-A)|=|E-A|=f1…ft=n+…0).
Рассмотрим матрицу:
Для
доказательства утверждения достаточно
показать, что SA.
Для этого найдем каноническую форму
|
= Докажем
единственность:
Алгоритм:
требуется построить матрицу в первой
нормальной форме, для заданной А, т.е.
1 K(E-A)=Diag (1,…,1,f1,…,ft) 2)
N1(A)= т.е нахождение 1-ой нормальной формы сводится к нахождению канонической формы. |
|
19. (1 из 6) Существование и единственность представления матрицы над полем во 2-й нормальной форме |
19. (2 из 6) Существование и единственность представления матрицы над полем во 2-й нормальной форме |
|
Определение:
Пусть
,
//
Теорема:
Пусть
◄
Пусть
Пусть
При этом:
|
Рассмотрим
сопровождающие матрицы
Рассмотрим
Найдем
|
|
19. (3 из 6) Существование и единственность представления матрицы над полем во 2-й нормальной форме |
19. (4 из 6) Существование и единственность представления матрицы над полем во 2-й нормальной форме |
|
Но
Тогда,
ЕДИНСТВЕННОСТЬ. ◄Пусть
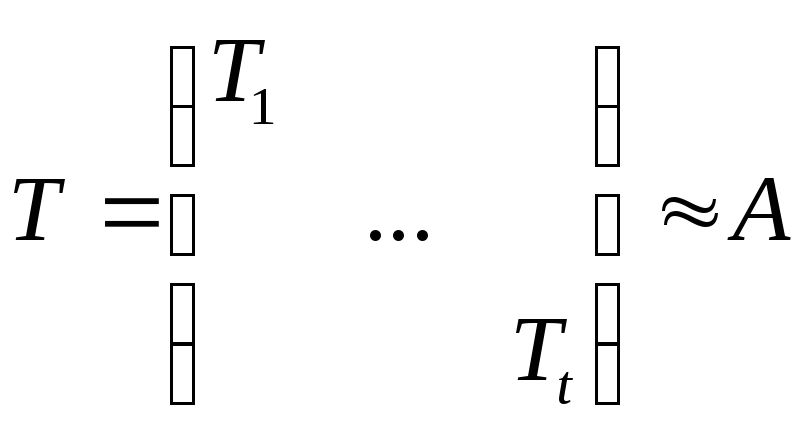
Построим матрицу N1(N2(A)).
|
ВНИМАНИЕ. В матрице ниже, мы сгруппировали сопровождающие матрицы следующим образом: взяли многочлен р1 минимальной степени и поместили его матрицу наверх, затем взяли многочлен р2 минимальной степени, и его матрицу поставили следующей по диагонали, и так далее до рк минимальной степени. Затем операция повторяется с оставшимися сопровождающими матрицами (смотри пример ниже). Рассмотрим
матрицу:
Т.к. приводимые преобразования однозначны, то и матрица N2(A) – единственна.► Пример:
|
|
19. (5 из 6)Существование и единственность представления матрицы над полем во 2-й нормальной форме |
19. (6 из 6) Существование и единственность представления матрицы над полем во 2-й нормальной форме |
|
Алгоритм.
Построение
Пусть
А – матрица над полем
|
Пример:
N1(A)=S(2+1)= Пример:
N1(A)=
|
|
20. (1 из 2) Минимальный многочлен линейного преобразования и способы его вычисления |
20. (2 из 2) Минимальный многочлен линейного преобразования и способы его вычисления |
|
Пусть
Пусть
//
Утверждение:
Множество аннулирующих многочленов является идеалом кольца многочленов. ◄Надо проверить: 1)
2)
Утверждение
2:
Определение:
1)
2)
3)
|
Определение:
Пусть
Тогда
◄Без доказательства►
Следствие:
Пусть
|
|
21. (1 из 4) Граф линейного преобразования линейного пространства над конечным полем. Циклы и деревья. |
21. (2 из 4) Граф линейного преобразования линейного пространства над конечным полем. Циклы и деревья. |
||
|
Пусть
Определение:
Пусть
О
|
здесь
поэтому
кол-во элементов
|
кол-во элементов
Пояснение:
//
Определение:
Пусть
1)
2)
Замечание:
В
|
Пример:
Определение:
Рассмотрим последовательность
элементов
а) если
б) если
Определение:
а) Подграф
|
|
21. (3 из 4) Граф линейного преобразования линейного пространства над конечным полем. Циклы и деревья. |
21.(4 из 4) Граф линейного преобразования линейного пространства над конечным полем. Циклы и деревья. |
|
1.
2.
б)
Определение:
Графы
|
Проверить на изоморфизм:
-
в графе такого преобразования нет
Утверждение:
Если
◄Пусть
Рассмотрим
Проверим
|

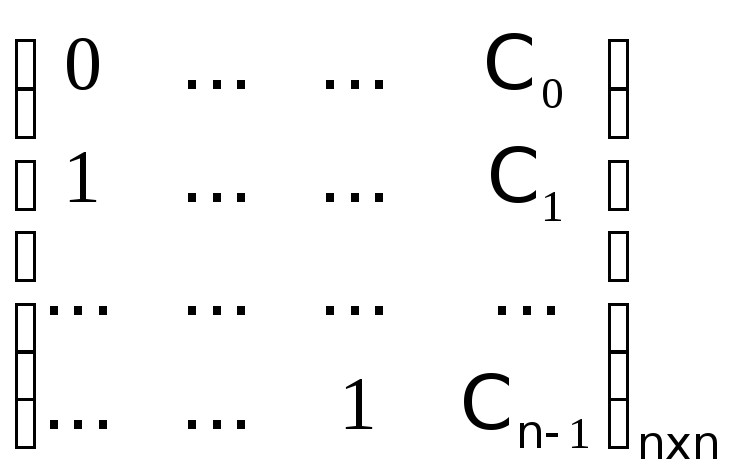 -
называется сопровождающей матрицей
многочлена f()=n-Cn-1n-1-…-C0,
f()P[],
P-поле
-
называется сопровождающей матрицей
многочлена f()=n-Cn-1n-1-…-C0,
f()P[],
P-поле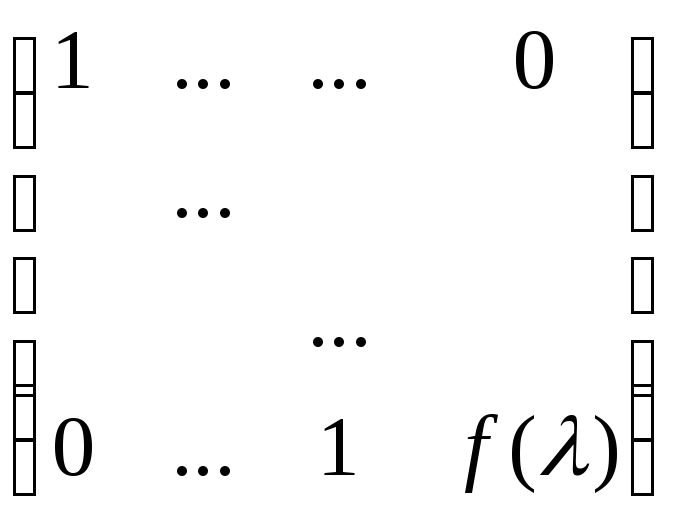
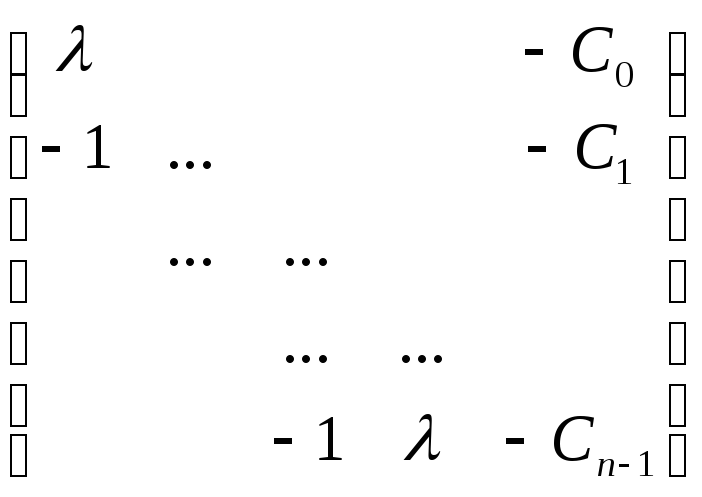
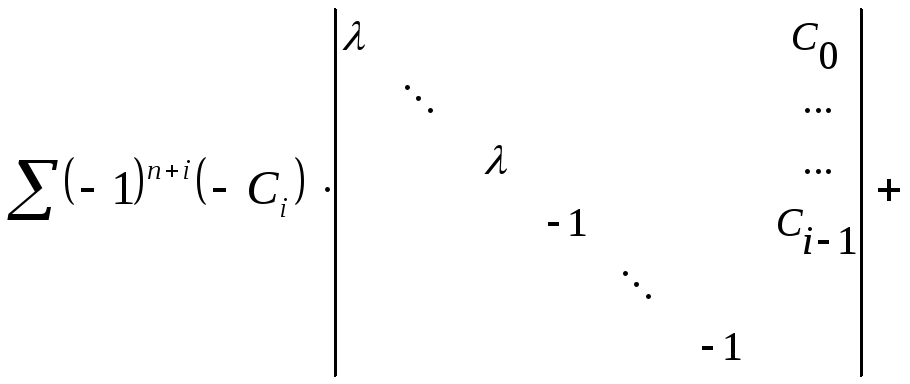
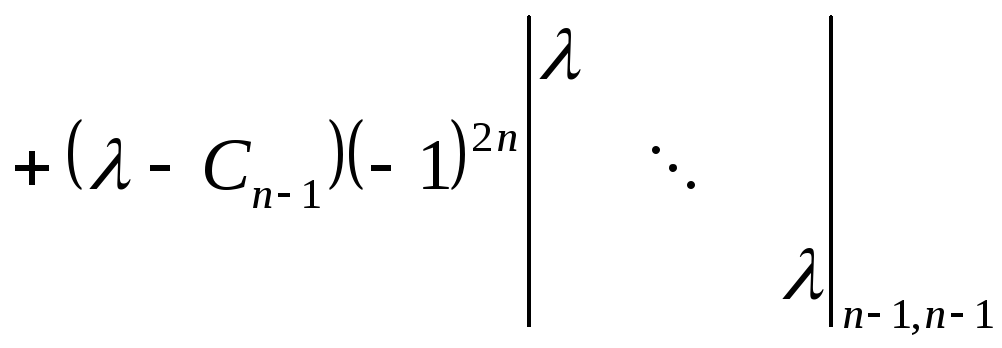 =
=(-Cn-1)n-1-
=
=(-Cn-1)n-1-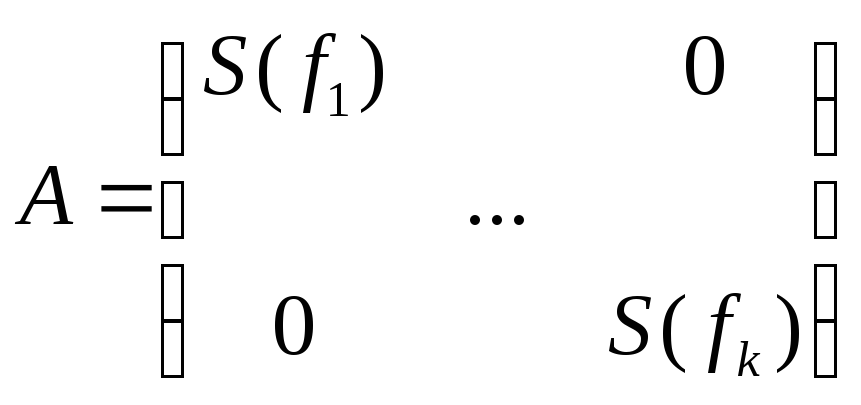 , где
, где
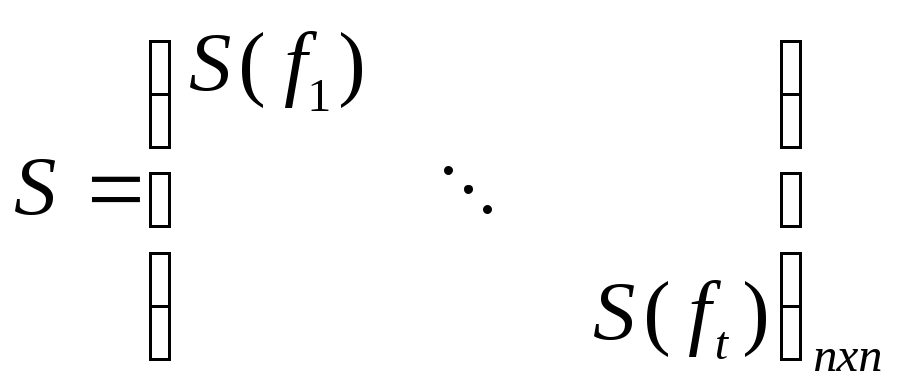
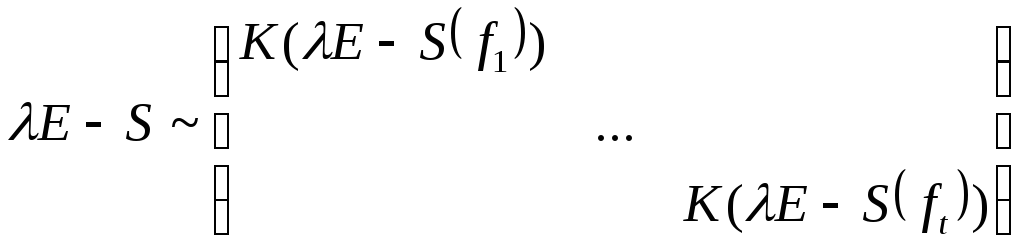 =
= ~
~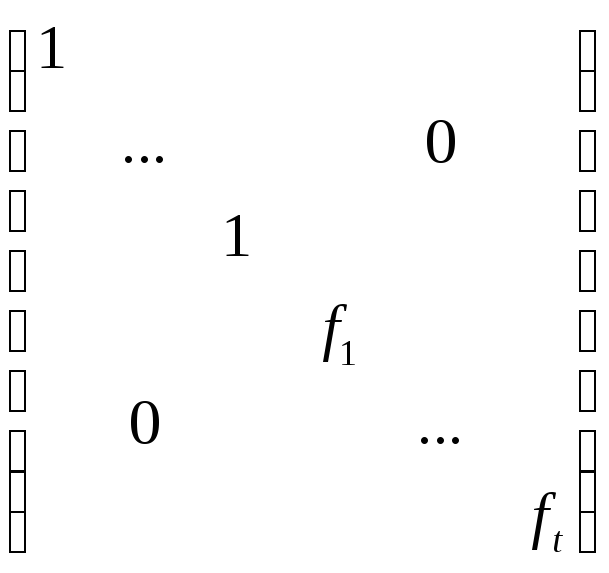 =K(E-S(f))=K(E-A)
AS,
но S
– в первой нормальной форме.
=K(E-S(f))=K(E-A)
AS,
но S
– в первой нормальной форме.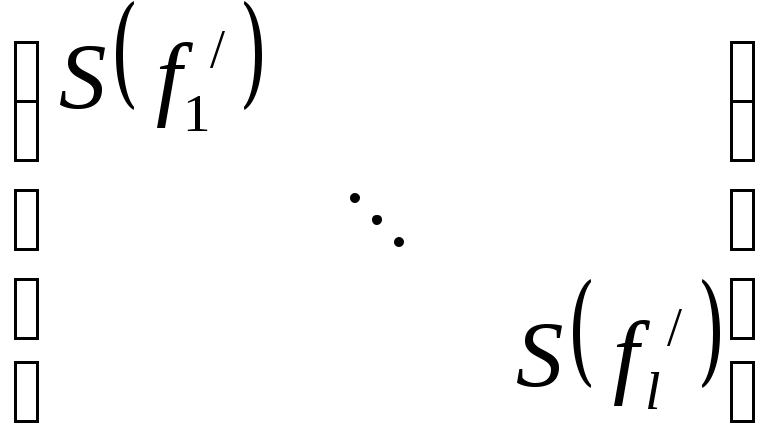 ,
S’≠S.
Тогда K(E-A)=Diag(1..1,f’1…f’ξ)=
=Diag(1…1,f1…ft)ξ=t
и f’i=fiS’=S
,
S’≠S.
Тогда K(E-A)=Diag(1..1,f’1…f’ξ)=
=Diag(1…1,f1…ft)ξ=t
и f’i=fiS’=S
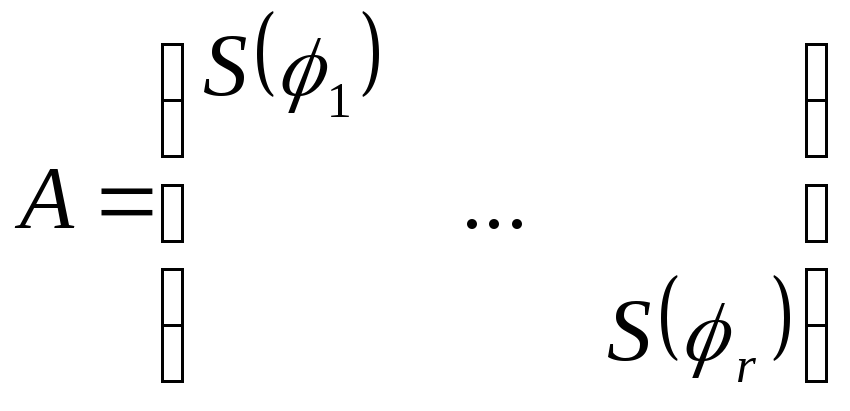 где
где
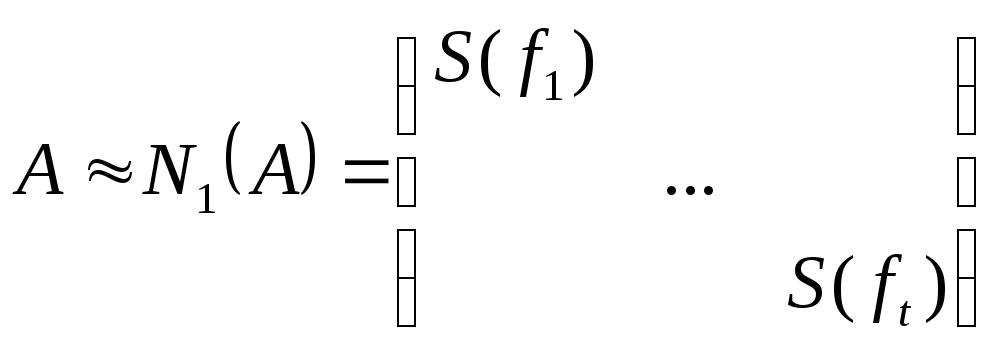 ,
где
,
где
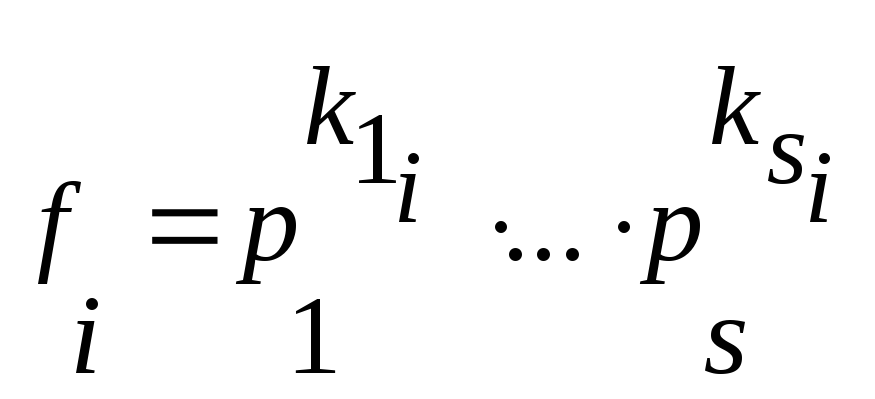 ,
,
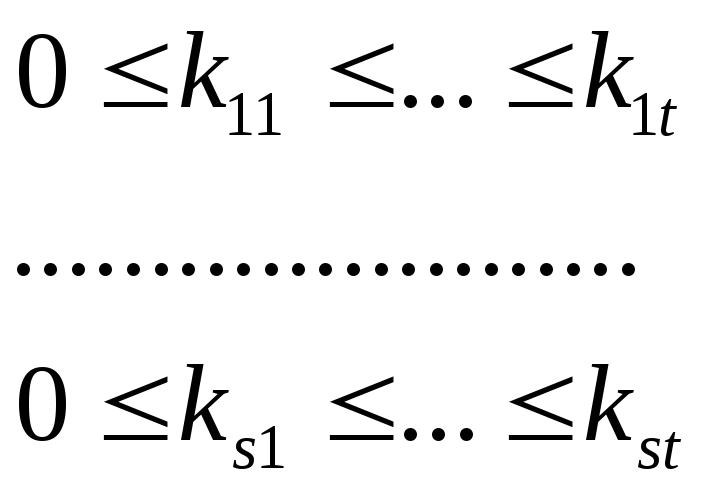 (*)
(*)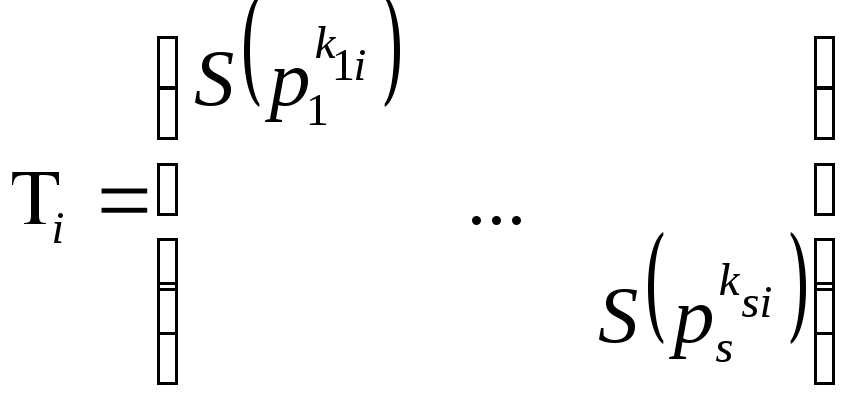 .
Покажем, что
.
Покажем, что
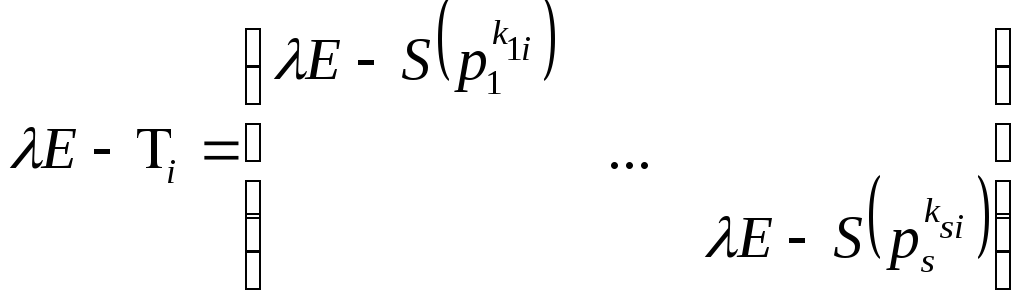

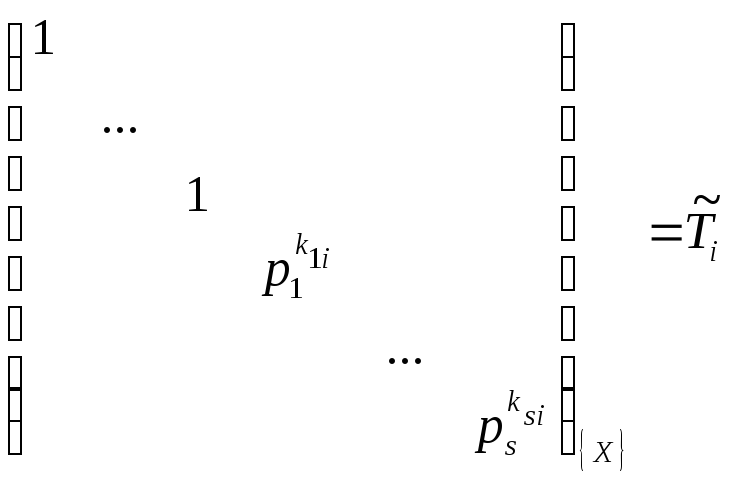
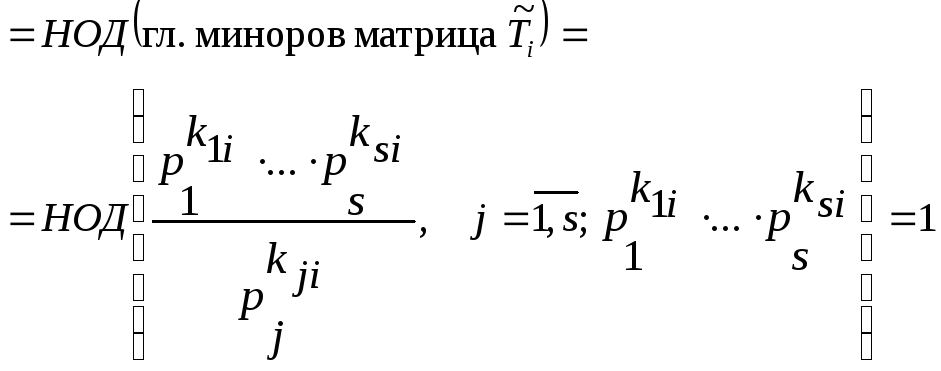
 ►
►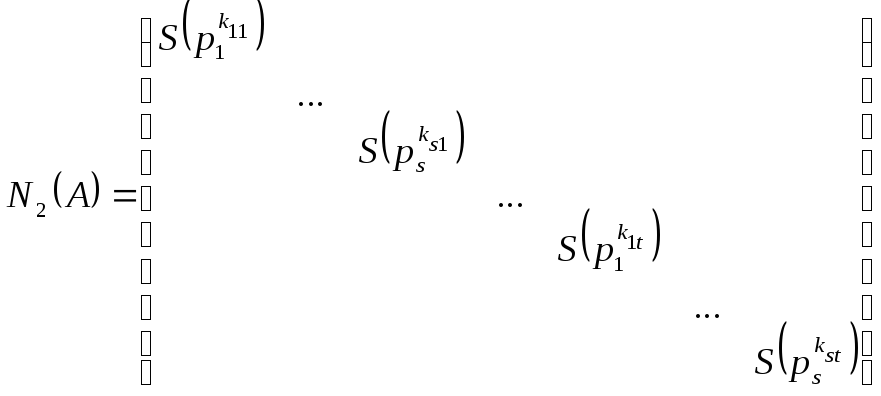 ,
где kij
удовлетворяет системе неравенств
(*), p1,…,ps
– неприводимые многочлены.
,
где kij
удовлетворяет системе неравенств
(*), p1,…,ps
– неприводимые многочлены.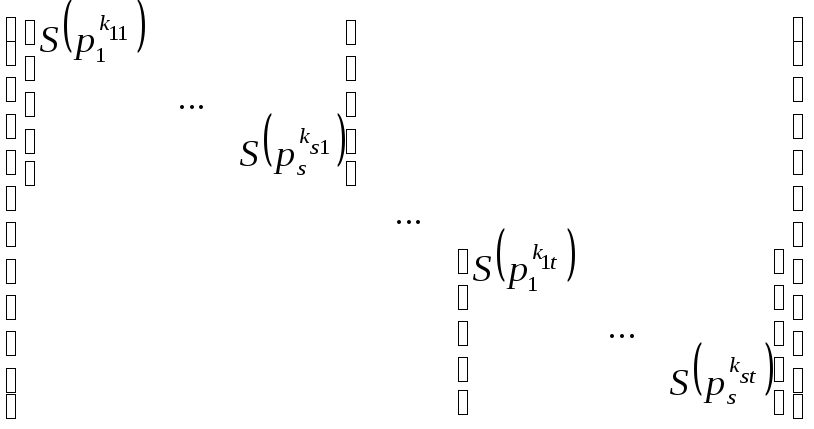
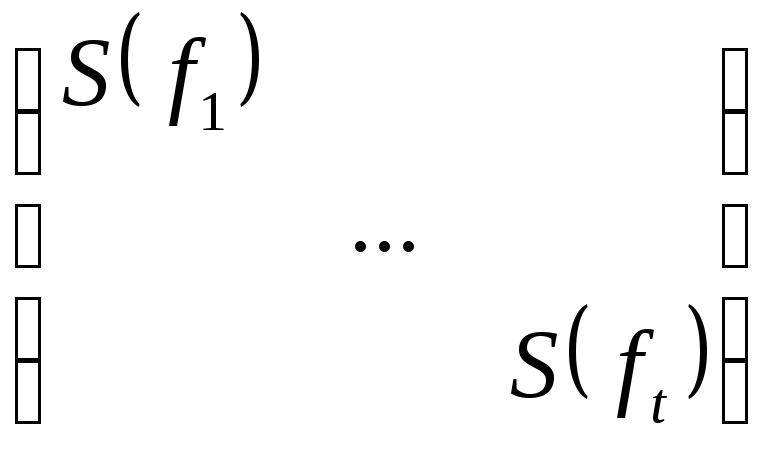
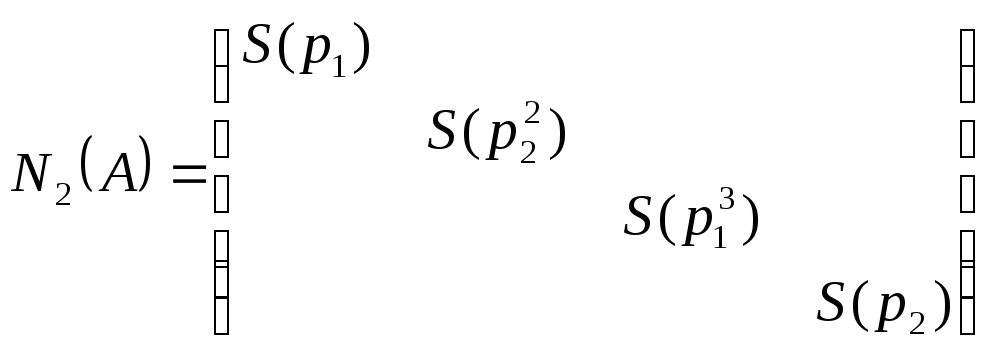
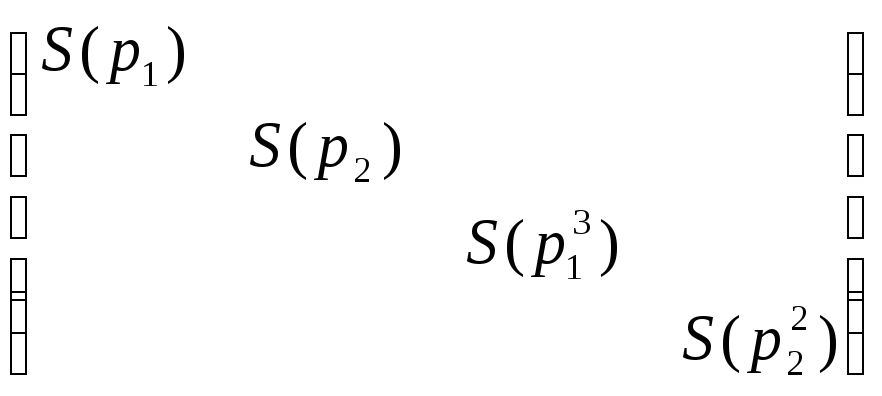
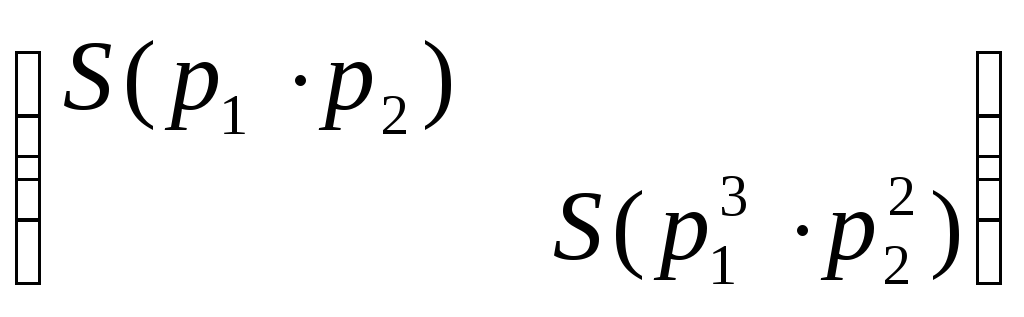
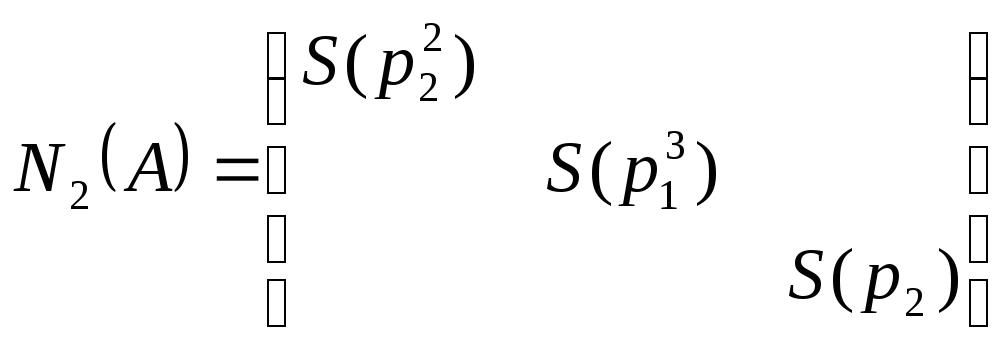
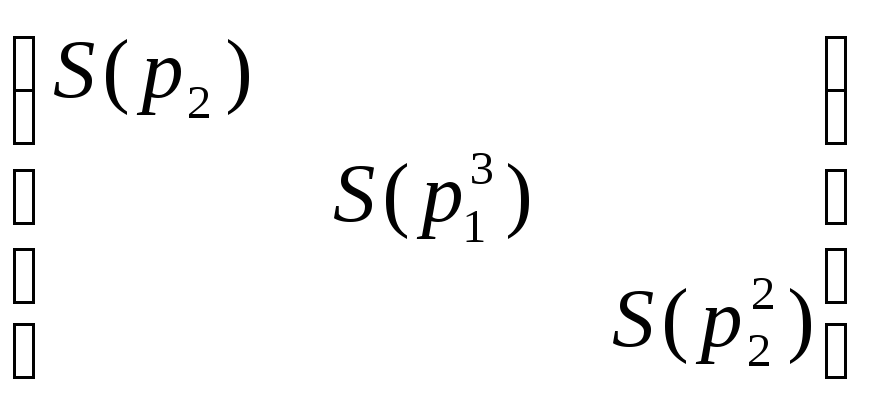
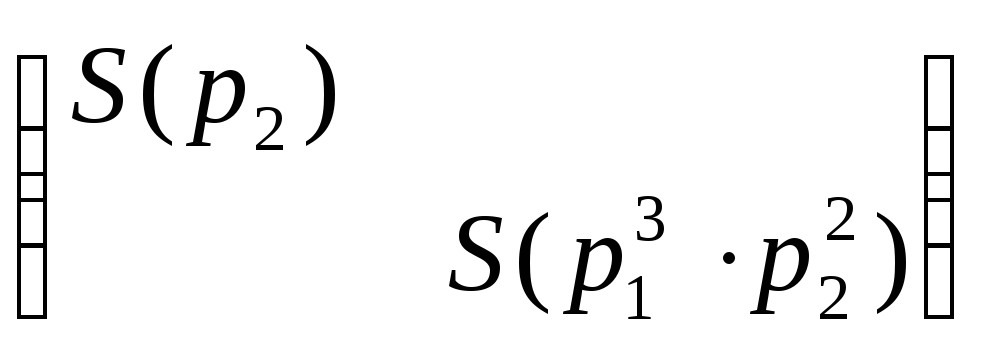
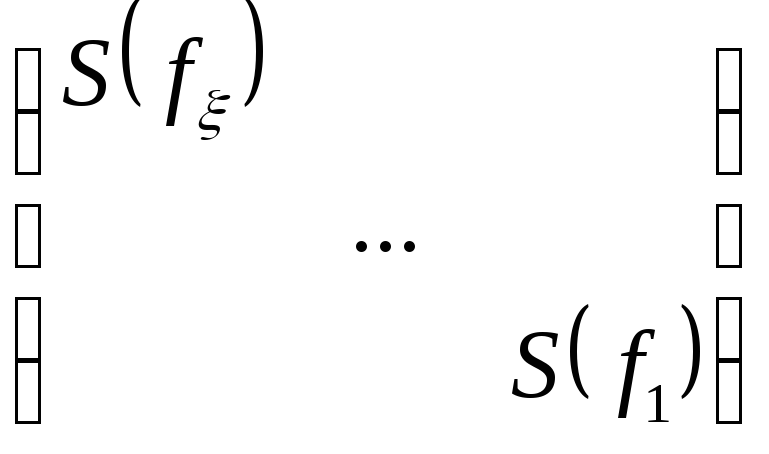
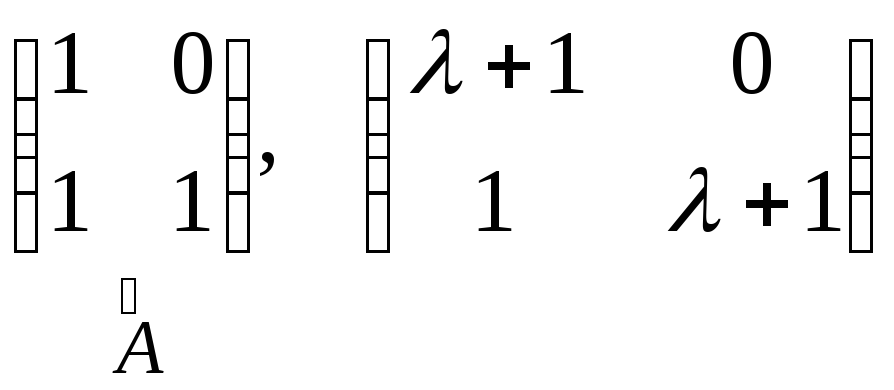
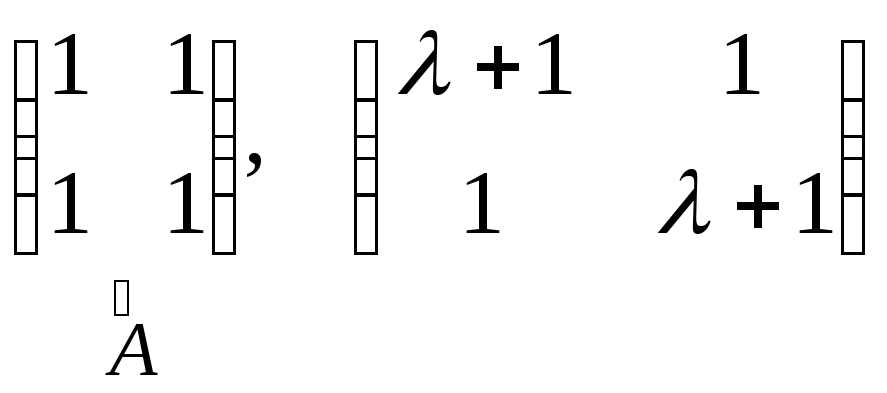
 - ориентированный граф.
- ориентированный граф.



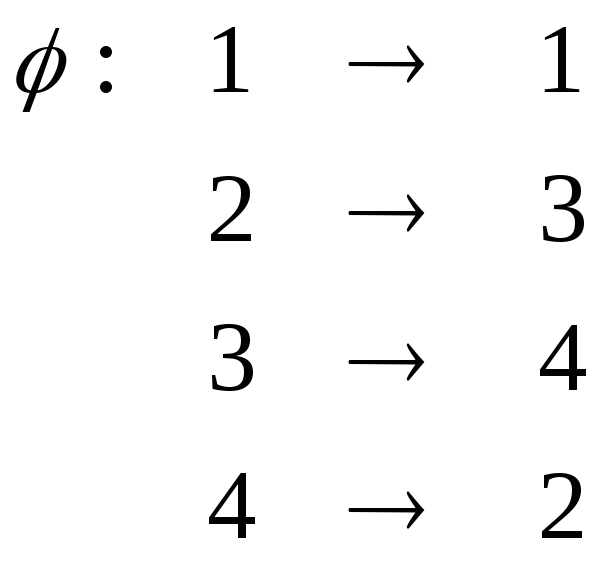


 ,
но
,
но