2.Информационные технологии в обучении математике.

Научные исследования последних лет свидетельствуют о необходимости внедрения компьютера в учебно-познавательную деятельность учащихся. Возможности, заложенные в нем, могут качественно изменить технологию школьного образовательного процесса. Компьютер становится эффективным средством обучения. Наличие многочисленных информационных сред и программ выдвигает перед педагогами одну из трудных проблем, связанную с выбором наиболее эффективных средств и методов обучения. Наша задача состоит в том, чтобы выяснить, какие из имеющихся информационных средств наиболее приспособлены для использования в процессе обучения учащихся математике. Для этого рассмотрим, например, различные способы визуализации поверхностей, заданных в трехмерном пространстве уравнением:

f(x, y)= sin( ).

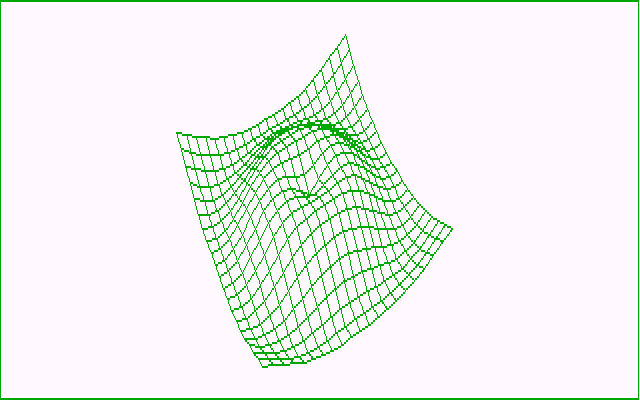
I. Построение графика функции осуществим сначала с помощью языка программирования Паскаль, который в последнее время считается одним из наиболее универсальных языков программирования.

Программа на языке Паскаль занимает четыре страницы машинописного текста и результат работы этой программы – изображение поверхности, представленное в виде прямоугольной сетки.

Целесообразно разработать программное обеспечение, позволяющее использовать компьютер как инструмент для решения задач без необходимости детального изучения языка программирования.

Получают распространение системы, ориентированные на решение определенного класса математических задач, не требующие специальной подготовки в области программирования, например, такие системы символьной математики, как Mathcad и Mathematica.

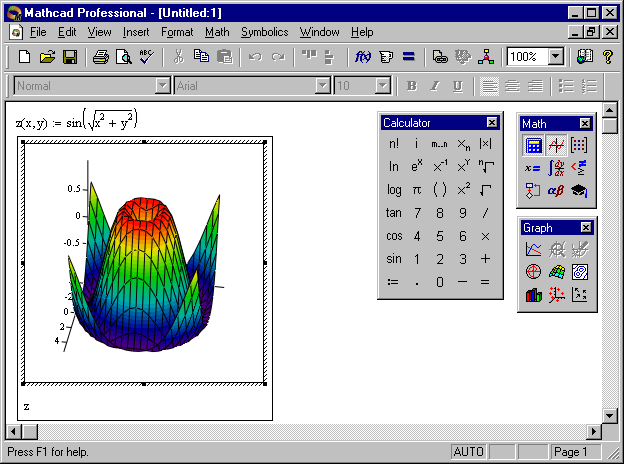
II. Построение объемных (трехмерных) графиков всегда было ахиллесовой пятой систем класса Mathcad. Связано это с тем, что такие графики даже в простейшем случае требуют создания матрицы точек зависимости z (x,y), то есть функции двух переменных. Создание такой матрицы нетривиальная задача, решение которой приводило не только к усложнению построений, но и к потере их наглядности. В новой версии Mathcad 2000 эта трудность была преодолена.

Построение графика осуществляем по следующему плану.

1. Определяем функцию z (x,y) двух переменных х и y.

2. Используя палитру графики, открываем шаблон трехмерной графики.

3. На единственное место ввода под шаблоном вводим z.

4. Отводим указатель мыши в сторону от графика и нажимаем левую кнопку мыши – строится график в виде “проволочного каркаса”.

График в виде “проволочного каркаса” не слишком эстетичен, хотя иногда и полезен, поскольку сквозь каркас видны обычно невидимые линии. Невидимые детали можно убрать, используя режим удаления невидимых линий. Это повышает внешнюю наглядность графика. Однако еще красочнее выглядят графики с функциональной окраской поверхности. Для ее получения проведем форматирование полученного графика. Наведем на график указатель и дважды щелкнем левой кнопкой. Появится довольно большое окно форматирования трехмерных графиков с множеством вкладок.

Открытая вкладка Special этого окна позволяет задать функциональную окраску поверхности. Для этого надо установить флажок Fill, снять флажок Auto Contour и увеличить до 30 значение в поле со счетчиком Number. Значение Z – Contours в раскрывающемся списке означает, что цвет окраски каждой точки поверхности является функцией от координаты z (высоты точки). Низко расположенные точки представляются темными цветами, а высоко – яркими. В принципе, возможен выбор ряда схем освещения поверхности, учет перспективы и т.д.

Итак, подобрав нужные параметры их можно проверить в деле. Располагаем окно форматирования так, чтобы была видна часть построенного графика. Тогда, щелкнув на кнопке Применить, можно увидеть, как повлияли введенные изменения на вид графика.

Если теперь отвести указатель мыши от графика и щелкнуть левой кнопкой, появится отформатированный график с функциональной цветной окраской.

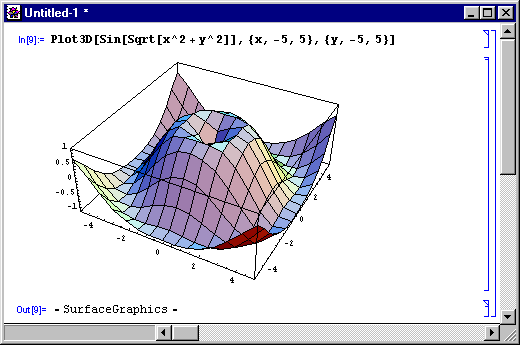
III. Для того, чтобы построить график заданной функции с помощью системы Mathematica, во входной строке помещаем название встроенной графической функции Plot3D, которая дает возможность получить изображение графика функции двух переменных вида z=f(x,y), саму функцию и промежутки рассмотрения переменных х и у. Затем нажимаем клавиши Shift+Enter и получаем изображение.

Сравнивая полученные графики и способы их получения, можно сделать вывод, что по простоте использования и по наглядности полученного изображения Паскаль и Mathcad значительно уступают системе символьной математики Matematica. К сказанному еще можно добавить, что Matematica уже успела себя зарекомендовать как высокоэффективное средство обучения. Компьютерная математическая система Mathematica получила широкое распространение в образовательных учреждениях многих стран. Начиная с 90-х годов, в них активно внедряется система обучения математике под названием “Mathematica: a system for doing mathematics by computer”. Система реализована на многих информационных платформах и представляет собой современную предметную среду с широким спектром возможностей в области обучения математике.