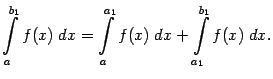- •2. Интегрирование подведением под знак дифференциала (см. Выше) и по частям. Интегралы, не берущиеся в элементарных функциях. (см. Выше)
- •4. Основные типы интегралов от элементарных дробей.
- •5. Интегралы, приводящиеся к интегралам от рациональных дробей, биноминальный дифференциал и подстановки Чебышева.
- •8. Суммы Дарбу и условия существования определенного интеграла.
- •9. Классы интегрируемых функций. Свойства определенных интегралов. Теоремы «о среднем».
- •11. Замена переменной в определенном интеграле, интегрирование по частям.
- •12. Площадь плоской фигуры и длина кривой в декартовых и полярных координатах, а также при параметрическом задании уравнений кривых.
- •13. Объем тела. Объем тела вращения и длина кривой в декартовых и полярных координатах и параметрически(см. Выше).
- •15. Несобственные интеграды. Интегралы с бесконечными пределами. Сходимость интеграла от неотрицательной функции. Признаки сходимости
- •16. Признаки сходиомсти несобственных интегралов. (см. Выше). 1-й и 2-й признаки сравнения интегралов. Абсолютная сходимость.
- •18. Признаки сходимости несобчтвенных интегралов от неограниченных фенкций. Признаки сравнения. См. Выше.
- •19. Определение линейного пространства. Элементы линейного пространства (вектора). Линейная зависимость и независимость между элементами. Базис и координаты.
- •20. Линейное пространство (см. Выше). Базис и координаты. (см. Выше). Размерность пространства (см. Выше).
- •21. Матрица и определители n-го порядка. Алгебраически едополнения и миноры.
- •22. Ранг матрицы. Теорема о базисном миноре и ее следствия. Методы вычисления ранга матрицы.
- •23. Система линейных кравнений. Решения системы однородных уравнений.
- •24. Неоднорродная система и ее совместность. Теорема Кронекера-Капелли.
- •25. Матричная алгебра. Сложение матриц и умножение матрицы на число. Перемножение матриц. Диагональная и единичная матрицы. Обратная матрица.
- •Умножение матриц Определение 14.4 Произведением матрицы размеровна матрицуразмеровназывается матрицаразмеров, элементы которой вычисляются по формуле
- •26. Матричная запись системы линейных уравнений (см. В 23). Решение систем в матричной форме (см. В 23)
- •27. Метод Гаусса решения системы линейных уравнений. (см. В 3)
- •28. Свойства определителей порядка n. Приведение определителя к треугольной и диагональной форме.
- •29. Элементарные преобразования матриц. Методы вычисления ранга матрицы (см. 22)
16. Признаки сходиомсти несобственных интегралов. (см. Выше). 1-й и 2-й признаки сравнения интегралов. Абсолютная сходимость.
Общий
признак сравнения.
Пусть на полупрямой
![]()
![]()
Тогда
из сходимости интеграла
![]() вытекает сходимость интеграла
вытекает сходимость интеграла![]() Доказательство.
Пусть
Доказательство.
Пусть
![]() сходится.
Тогда, согласно критерию Коши, для
любого
сходится.
Тогда, согласно критерию Коши, для
любого![]() найдется
такое В>а, что для любых А1>В и А2>В
выполняется неравенство
найдется
такое В>а, что для любых А1>В и А2>В
выполняется неравенство .Согласно
известным неравенствам для интегралов
и неравенству
.Согласно
известным неравенствам для интегралов
и неравенству![]() получим
получим
![]() Отсюда
и из
неравенства
Отсюда
и из
неравенства
 вытекает,
что для любых А1>В
и
А2>В
справедливо
неравенство
вытекает,
что для любых А1>В
и
А2>В
справедливо
неравенство![]() .
Следовательно, интеграл
.
Следовательно, интеграл![]() сходится.
сходится.
Частный
признак сравнения.
Пусть
на полупрямой
![]() функция
f(x)
удовлетворяет соотношению
функция
f(x)
удовлетворяет соотношению
![]() ,
где
с и
,
где
с и
![]() —
постоянные,
—
постоянные,
![]() >1.
Тогда
интеграл
>1.
Тогда
интеграл![]() сходится.
Если же существует такая постоянная
с>0,
что
на полупрямой
сходится.
Если же существует такая постоянная
с>0,
что
на полупрямой
![]() справедливо
соотношение
справедливо
соотношение
![]() ,
в котором
,
в котором
![]() ,то
интеграл
,то
интеграл
![]() расходится.
расходится.
Утверждение этой теоремы вытекает из утверждения общего признака сравнения. Абсолютная и условная сходимость несобственных интегралов. Введем понятия абсолютной и условной сходимости интегралов. Пусть f(x) интегрируема по любому сегменту [а, A] .
Определение
1. Несобственный интеграл
![]() называется
абсолютно сходящимся, если сходится
называется
абсолютно сходящимся, если сходится![]()
Определение
2. Несобственный интеграл
![]() называется условно сходящимся,
если он сходится, а ин-теграл
называется условно сходящимся,
если он сходится, а ин-теграл![]() расходится.
расходится.
17. Несобственные интегралы от функций, имеющих ращрыв второго рода. Признаки сходиомсти (+см. выше).
Несобственным интегралом второго рода назовём тогда интеграл
![]() значение
значение
![]() которого
равняется левостороннему пределу
которого
равняется левостороннему пределу Если
этот предел существует, то несобственный
интеграл называетсясходящимся,
а если предела не существует, то
расходящимся.
Расходящемуся интегралу не приписывается
никакого числового значения; в этом
случае будем условно писать
Если
этот предел существует, то несобственный
интеграл называетсясходящимся,
а если предела не существует, то
расходящимся.
Расходящемуся интегралу не приписывается
никакого числового значения; в этом
случае будем условно писать
 Геометрически
вычисление несобственного интеграла
второго рода представляет собою (при
Геометрически
вычисление несобственного интеграла
второго рода представляет собою (при![]() )
исчерпание плошади неограниченной
фигуры под графиком функции
)
исчерпание плошади неограниченной
фигуры под графиком функции![]() над
над![]() с
помощью вычисления плошадей ограниченных
фигур, получающихся над отрезком
с
помощью вычисления плошадей ограниченных
фигур, получающихся над отрезком![]() ,
а затем приближением правого конца
,
а затем приближением правого конца![]() к
точке
к
точке![]() (см. рис.).
(см. рис.).
 Итак,
площадь неограниченной фигуры,
изображённой на рисунке, по
определению
равна значению несобственного интеграла
Итак,
площадь неограниченной фигуры,
изображённой на рисунке, по
определению
равна значению несобственного интеграла
![]() .
.
Аналогично интегралу
по полуинтервалу
![]() от
функции
от
функции![]() с
особенностью в точке
с
особенностью в точке![]() ,
определяется несобственный интеграл
второго рода от функции
,
определяется несобственный интеграл
второго рода от функции![]() ,
имеющей особенность в точке
,
имеющей особенность в точке![]() полуинтервала
полуинтервала![]() :
:![]() если
существует предел
если
существует предел В
случае существования указанного предела
интеграл называетсясходящимся,
а в случае, когда предел не существует, --
расходящимся.
Свойства несобственных интегралов
второго рода
В
случае существования указанного предела
интеграл называетсясходящимся,
а в случае, когда предел не существует, --
расходящимся.
Свойства несобственных интегралов
второго рода
Свойства
несобственных интегралов второго рода,
по сути дела, повторяют свойства
несобственных интегралов первого рода:
меняется лишь база предела, задающего
несобственный интеграл, с
![]() для
интеграла
для
интеграла на
на![]() для
интеграла от функции с особенностью в
точке
для
интеграла от функции с особенностью в
точке![]() :
: Теорема
4.5
Пусть
фиксированы числа
Теорема
4.5
Пусть
фиксированы числа
![]() и
функция
и
функция![]() интегрируема
на любом отрезке
интегрируема
на любом отрезке![]() ,
где
,
где![]() ,
и имеет особенность в точке
,
и имеет особенность в точке![]() .
Тогда если несобственный интеграл
.
Тогда если несобственный интеграл сходится,
то при любом
сходится,
то при любом![]() сходится
интеграл
сходится
интеграл![]() .
Обратно, если при некотором
.
Обратно, если при некотором![]() сходится
интеграл
сходится
интеграл![]() ,
то сходится и интеграл
,
то сходится и интеграл![]() .
Доказательство.
Докажем, что из сходимости
.
Доказательство.
Докажем, что из сходимости
![]() следует
сходимость
следует
сходимость![]() при
при![]() .
Из аддитивности интеграла следует, что
при любом
.
Из аддитивности интеграла следует, что
при любом![]() имеет
место равенство
имеет
место равенство
|
|
(4.4*) |
Переходя
в этом равенстве к пределу при
![]() ,
получаем:
,
получаем:
|
|
|
причём
несобственный интеграл в правой части
сходится по условию теоремы, а интеграл
 --
постоянное слагаемое. Значит, предел,
задающий интеграл
--
постоянное слагаемое. Значит, предел,
задающий интеграл![]() ,
существует и равен
,
существует и равен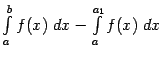 .
Докажем второе утверждение теоремы,
используя формулу (4.4*).
По условию теоремы интеграл по отрезку
.
Докажем второе утверждение теоремы,
используя формулу (4.4*).
По условию теоремы интеграл по отрезку
![]() ,
не содержащему особенностей функции,
существует, так что при любом
,
не содержащему особенностей функции,
существует, так что при любом![]() из
формулы (4.4*)
получаем:
из
формулы (4.4*)
получаем:
|
|
|
Перейдём
к пределу при
![]() и
получим, что
и
получим, что
|
|
|
Теорема
4.6
(теоpема сpавнения) Пусть даны две
функции
![]() и
и![]() ,
заданные на
,
заданные на![]() и
имеющие особенность в точке
и
имеющие особенность в точке![]() ,
причём при всех
,
причём при всех![]() выполняется
неравенство
выполняется
неравенство![]() Тогда из
сходимости интеграла от большей функции
следует сходимость интеграла от меньшей
функции, причём
Тогда из
сходимости интеграла от большей функции
следует сходимость интеграла от меньшей
функции, причём
|
|
(4.5) |
а из расходимости интеграла от меньшей функции, следует расходимость интеграла от большей функции:

Теорему
4.6 можно
использовать для исследования сходимости
интегралов, не вычисляя их значений.
Теорема 4.7
Пусть
функция
![]() имеет
особенность в точке
имеет
особенность в точке![]() .
Если интеграл
.
Если интеграл
 сходится,
то сходится также интеграл
сходится,
то сходится также интеграл![]() причём
имеет место неравенство
причём
имеет место неравенство
![]() Определение
4.8
Пусть функция
Определение
4.8
Пусть функция
![]() обладает
теми же свойствами, что в предыдущей
теореме. Если несобственный интеграл
обладает
теми же свойствами, что в предыдущей
теореме. Если несобственный интеграл![]() сходится,
то несобственный интеграл
сходится,
то несобственный интеграл![]() называетсяабсолютно
сходящимся.
Если несобственный интеграл
называетсяабсолютно
сходящимся.
Если несобственный интеграл
![]() расходится,
а несобственный интеграл
расходится,
а несобственный интеграл![]() сходится,
а несобственный интеграл
сходится,
а несобственный интеграл![]() называетсяусловно
сходящимся.
Предыдущая теорема означает, что любой
абсолютно сходящийся интеграл является
сходящимся. Теорема
4.8
Пусть для
функции
называетсяусловно
сходящимся.
Предыдущая теорема означает, что любой
абсолютно сходящийся интеграл является
сходящимся. Теорема
4.8
Пусть для
функции
![]() ,
имеющей особенность в точке
,
имеющей особенность в точке![]() и
интегрируемой на любом отрезке
и
интегрируемой на любом отрезке![]() ,
где
,
где![]() ,
существует мажоранта
,
существует мажоранта![]() на
на![]() ,
причём несобственный интеграл
,
причём несобственный интеграл![]() сходится.
Тогда несобственный интеграл
сходится.
Тогда несобственный интеграл![]() тоже
сходится, и
тоже
сходится, и![]() .
.