23. Система линейных кравнений. Решения системы однородных уравнений.

Системой линейных уравнений с неизвестными называется система уравнений вида

(15.1)

Система уравнений называется однородной, если инеоднородной в противном случае. Систему (15.1) можно записать также в виде или в виде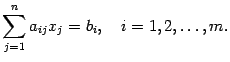Но наиболее удобной формой записи системы (15.1) является матричная запись. Введем следующие матрицы: матрица системы , столбец неизвестныхи столбец свободных членов,

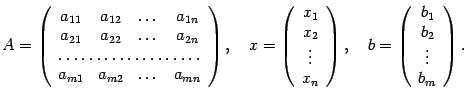
Систему (15.1) можно записать в виде

(15.2)

Определение 15.2   Решением системы (15.1) называется любой набор чисел , которые при подстановке в систему вместо неизвестныхпревращаютвсе уравнения системы в верные равенства. Решением системы (15.2) называется столбец чисел , который после подстановки в уравнение вместо столбцапревращает уравнение (15.2) в верное матричное равенство. Однородная система уравнений

(15.7)

всегда является совместной. Доказательство.    Для этой системы набор чисел ,,,является решением. Будем использовать матричную запись системы:. Предложение15.3   Сумма решений однородной системы линейных уравнений является решением этой системы. Решение, умноженное на число, тоже является решением. Доказательство.     Пусть ислужат решениями системы. Тогдаи. Пусть. ТогдаТак как, то-- решение. Пусть-- произвольное число,. ТогдаТак как, то-- решение. Следствие15.1   Если однородная система линейных уравнений имеет ненулевое решение, то она имеет бесконечно много различных решений. Действительно, умножая ненулевое решение на различные числа, будем получать различные решения. Определение 15.5   Будем говорить, что решения системыобразуютфундаментальную систему решений, если столбцы образуют линейно независимую систему и любое решение системы является линейной комбинацией этих столбцов. Определение15.6   Пусть -- фундаментальная система решений однородной системы. Тогда выражениегде-- произвольные числа, будем называтьобщим решением системы . Из определения фундаментальной системы решений следует, что любое решение однородной системы может быть получено из общего решения при некоторых значениях. И наоборот, при любых фиксированных числовых значенияхиз общего решения получим решение однородной системы. Теорема15.3   Пусть -- фундаментальная система решений однородной системы. Тогда, где-- число неизвестных в системе.Структура решений неоднородной системы линейных уравнений, Систему неоднородных уравнений запишем в матричном виде , где матрицаимеет размеры. Предложение 15.4Пусть и-- решения неоднородной системы. Тогда их разностьявляется решением однородной системы с той же матрицей, то есть решением системы. Доказательство.     По условию и. ТогдаТак как, то-- решение однородной системы. Предложение 15.5Пусть -- решение неоднородной системы,-- любое решение однородной системы. Тогда-- решение неоднородной системы.Определение 15.7   Пусть -- некоторое решение неоднородной системы линейных уравнений,-- общее решение однородной системы. Тогда выражениеназываетсяобщим решением неоднородной системы. Учитывая запись общего решения однородной системы через фундаментальную систему ее решений , получаем для общего решения неоднородной системы формулуИз двух последних предложений следует, что любое решение неоднородной системы может быть получено из общего решения при некоторых числовых значениях коэффициентов. Теорема 15.4Система линейных уравнений может иметь либо бесконечно много решений, либо одно решение, либо не иметь решений. Доказательство.     Пусть система имеет решение . Если однородная системаимеет только одно решение, то из формулы общего решения будет следовать, что-- единственное решение неоднородной системы. Если однородная система имеет хотя бы одно ненулевое решение, то ее фундаментальная система решений будет состоять не менее, чем из одного решения. В формуле общего решения неоднородной системы будет произвольный коэффициент, и при различных его значениях мы будем получать различные решения неоднородной системы.