4. Основные типы интегралов от элементарных дробей.

Определение: Элементарными называются дроби следующих четырех типов: I.  III.   II.  IV. 

m, n – натуральные числа (m  2, n  2) и b² – 4ac <0. Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.

I.

 II. 

Рассмотрим метод интегрирования элементарных дробей вида III.

Интеграл дроби вида III может быть представлен в виде:

Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам. Рассмотрим теперь методы интегрирования простейших дробей IV типа. Сначала рассмотрим частный случай при М = 0, N = 1. Тогда интеграл вида  можно путем выделения в знаменателе полного квадрата представить в виде . Сделаем следующее преобразование:.

Второй интеграл, входящий в это равенство, будем брать по частям. Обозначим: Для исходного интеграла получаем: Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл . Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае В полученном равенстве первый интеграл с помощью подстановки t = u² + s приводится к табличному , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.

5. Интегралы, приводящиеся к интегралам от рациональных дробей, биноминальный дифференциал и подстановки Чебышева.

Интегралы, сводящиеся к интегралам от рациональных функций Некоторые типы неопределённых интегралов сводятся путём соответствующей замены к интегралам от рациональных функций. Рассмотрим три таких случая. Определение 2.1   Будем говорить, что функция рациональным образом зависит от выражения , еслиможно представить в видегде-- рациональная функция от переменного.Одночленом от двух переменных иназовём выражение вида, где, а показатели степении-- целые неотрицательные числа.Многочленом от двух переменных иназовём сумму конечного числа одночленом от этих двух переменных. (Считаем, что сумма может состоять и из одного слагаемого, так что каждый одночлен -- это частный случай многочлена.)Рациональной функцией от двух переменных иназовём отношение двух многочленов оти:гдеи-- многочлены оти.Определение 2.2   Будем говорить, что функция рациональным образом зависит от выражений и, еслиможно представить в видегде-- рациональная функция от переменныхи. 1.Интегралы от функций, рациональным образом зависящих от экспоненты. Рассмотрим интегралы вида где-- рациональная функция. Сделаем естественную замену. Тогдаи. Получаем:где. Заметим, что-- это тоже рациональная функция, так как-- тоже многочлен. Таким образом, мы свели дело к вычислению интеграла от рациональной функции, после нахождения которого нужно сделать заменуи получить ответ. 2.Интегралы от функций, рациональным образом зависящих от и. Рассмотрим интегралы видагде-- рациональная функция от двух переменныхи, а выраженияитаковы:,, и. Такие интегралы приводятся к интегралам от рациональных функций одного переменного, если сделать естественную замену. Действительно, тогдаи, а интеграл приводится к видугдеНетрудно заметить, что функциярационально зависит от единственного своего аргумента. Заметим, что точно та же замена годится и в случае, когда подынтегральная функция зависит рациональным образом только от. 3.Интегралы от функций, рациональным образом зависящих от и. Интегралы вида где-- функция, рациональным образом зависящая оти, можно привести к интегралу от рациональной функции от одного переменного, если сделать так называемую "универсальную" заменуПри этоми, откудаС помощью этих формул исходный интеграл преобразуется к видугдеНетрудно заметить, что-- рациональная функция одного переменного. Если имеет место частный случай рациональной зависимости оти, когда обе эти функции входят в выражение лишь в чётных степенях, то есть подынтегральная функция имеет видто применять универсальную замену не обязательно: она, как правило, будет приводить к слишком сложным интегралам; в этих случаях гораздо лучше применить другую тригонометрическую замену:В этом случаеи, откудаЗамечание 2.5   Замена годится также в случае интеграла, в котором функциярациональным образом зависит отии обладает следующим свойством:Тогда при замене нужно использовать формулыЕсли же подынтегральная функциязависит от своих аргументов несимметричным образом, то ничего не остаётся делать, как применять не всегда приятную универсальную замену.Биномиальный дифференциал. Бином Ньютона – это формула, выражающая выражение (a + b)ⁿ  в виде многочлена. Эта формула имеет вид:  - число сочетаний из п элементов по k. _. Когда степень бинома невысока, коэффициенты многочлена могут быть найдены не расчетом по формуле количества сочетаний, а с помощью так называемого треугольника Паскаля.  Этот треугольник имеет вид:

1

1 2 1

1 3 3 1

1 4 6 4 1 Формула бинома Ньютона может быть обобщена для произвольного числа слагаемых. _{Подстановки Чебышева.} Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях: 1)      Если р – целое число, то интеграл рационализируется с помощью подстановки , где  - общий знаменатель m и n. 2)      Если  - целое число, то интеграл рационализируется подстановкой , где s – знаменатель числа р. 3) Если  - целое число, то используется подстановка , где s – знаменатель числа р. Однако, наибольшее практическое значение имеют интегралы от функций, рациональных относительно аргумента и квадратного корня из квадратного трехчлена. На рассмотрении этих интегралов остановимся более подробно. Интегралы вида . Существует несколько способов интегрирования такого рода функций. В зависимости от вида выражения, стоящего под знаком радикала, предпочтительно применять тот или иной способ. Как известно, квадратный трехчлен путем выделения полного квадрата может быть приведен к виду: Таким образом, интеграл приводится к одному из трех типов:1) 2)  3) 1 способ. Тригонометрическая подстановка. Теорема: Интеграл вида  подстановкой  или  сводится к интегралу от рациональной функции относительно sint или cost. Теорема: Интеграл вида  подстановкой  или сводится к интегралу от рациональной функции относительно sint и cost. Теорема: Интеграл вида  подстановкой  или  сводится к интегралу от рациональной функции относительно sint или cost.

6. Интегрирование тригонометрических выражений с помощью подстановок t=tg(x/2) и t=tg(x). Задача о площади криволинейной трапеции. Интегральная сумма и определенный интеграл Римана.Интегралы от функций, рациональным образом зависящих от иИнтегралы вида где-- функция, рациональным образом зависящая оти, можно привести к интегралу от рациональной функции от одного переменного, если сделать так называемую "универсальную" заменуПри этоми, откудаС помощью этих формул исходный интеграл преобразуется к видугдеНетрудно заметить, что-- рациональная функция одного переменного. Если имеет место частный случай рациональной зависимости оти, когда обе эти функции входят в выражение лишь в чётных степенях, то есть подынтегральная функция имеет видто применять универсальную замену не обязательно: она, как правило, будет приводить к слишком сложным интегралам; в этих случаях гораздо лучше применить другую тригонометрическую замену:В этом случаеи, откуда. Задача о нахождении площади плоской области, ограниченной на координатной плоскостиотрезкомоси, графиком непрерывной функции, заданной на отрезке, и двумя отрезками вертикальных прямыхи, соединяющими точки осис точками графика. Сначала попробуем найти значение искомой площади приближённо. Для этого разделим областьна узкие вертикальные полоски, проведя вертикальные линии; при этом мы будем считать, чтоТогда областьлежит между прямымии, где. Обозначим длины отрезков между такими прямыми через:. Очевидно, что площадьобластилежит в пределах отдо, гдеи, и примерно равна, где-- произвольная точка отрезка. Легко видеть также, что при любом выборе точекмы получаемТогда искомая площадьприблизительно равна сумме величин:и лежит между суммой площадейи:. При любом выборе точекполучаем. Если все отрезки деления имеют малые длины, то в силу непрерывности функции все разности междуибудут также малы. Точнее говоря, для любого, как угодно малогоможно найти такое, что прибудетпри всех. Значит, разница между правой и левой частями будет меньше, чемПоскольку приэта величина стремится к 0, то левые и правые части неравенств имеют общий предел, который равен. По теореме "о двух милиционерах" величинатакже имеет пределом число-- искомую площадь области. Теперь заметим, что составить суммумы можем не только для положительной непрерывной функции, но для произвольной функции, заданной на. Разберёмся теперь с тем, от какой величины и при каком условии вычисляется упомянутый предел, то есть какова база предела. Величиназависит, в силу своего определения, во-первых, от выбора точек, которые делят на части отрезок, то есть от набора точек, где, а также от выбора промежуточных точек, в которых вычисляются значения функции, то есть набора точек, где. Наборыизадаютразмеченное разбиение отрезка : точкизадаютразбиение, а точки --разметку этого разбиения. Итак, при фиксированной функции величиназависит от размеченного разбиения:Величинаназываетсяинтегральной суммой, построенной для функции на отрезкепо размеченному разбиению; интегральная сумма является функцией от размеченного разбиения и определена на множестве всех размеченных разбиений. Величина, равная длине самого большого из отрезков разбиения, называетсядиаметром разбиения; то же относится и к размеченному разбиению . Диаметр размеченного разбиениябудем обозначатьили. Итак,

Если длина каждого из отрезков разбиения меньше некоторого числа , то это означает, что. Рассмотрим множество всех размеченных разбиений отрезка. При любом значениисуществуют разбиения с диаметром, меньшим. Достаточно, например, поделить отрезок наравных частей, взяв достаточно большое число этих частей:Значит, множестворазмеченных разбиений с диаметром, меньшим, не пусто при любом. Если взять два значения, скажем,, то очевидно, что каждое разбиение диаметра меньше, одновременно имеет диаметр меньше, так что, если. Так что. Вспомним теперь определение базы произвольного предела: базасостоит из окончаний, таких что все они непусты и если, то существует третье окончание, такое что. Наши множества разбиений, как мы только что проверили, образуют некоторую базу в множестве всех разбиений отрезка. Действительно, мы проверили, что они непусты и приив качествеможно взять, если. Итак, размеченные разбиения образуют базув том самом множестве, для элементов которого определены значения интегральной суммы. Эту базу мы будем обозначать. Когда мы берём размеченные разбиения со всё меньшим и меньшим диаметром, мы измельчаем деление отрезка на части, и при этом интегральная сумма может иметь предел, который, в случае положительной непрерывной функции, равен площади криволинейной трапеции. Эти соображения приводят нас к следующему основному определению.Определение 3.1   Для заданной функции на отрезкеназовёмопределённым интегралом от почисло, равное пределу интегральной суммы, рассматриваемой как функция размеченного разбиения, по базе. Определённый интеграл обозначается. Итак,

Если функция такова, что определённый интеграл от неё по отрезкусуществует (то есть если интегральная сумма имеет предел при базе), то функцияназываетсяинтегрируемой на отрезке . По отношению к интегралучислоназываетсянижним пределом, число --верхним пределом, а функция --подынтегральной функцией. Если вспомнить общее определение предела и записать его применительно к нашему случаю, то получим, что число равно определённому интегралу отпо отрезку, если для любого, сколь угодно малого числамы можем выбрать такое число, задающее мелкость разбиения, что для любого размеченного разбиенияс диаметром, меньшим, значение интегральной суммы будет отличаться от числане больше чем на:

если Заодно, кроме общего определения определённого интеграла, мы получили определение площадикриволинейной трапеции, лежащей под графиком функции, как такого же предела интегральных сумм: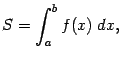

если функция непрерывна наипри всех. Сделаем ещё такое важное замечание: в обозначениисовершенно неважно, какой именно буквой обозначена переменная интегрирования (в данном случае): если фиксированы подынтегральная функцияи пределы интегрированияи, то интегралы,,и т. п. означают одно и то же число, к которому стремятся интегральные суммы, построенные для функциина отрезкепри измельчении размеченного разбиения. Рассматривая на каждом из отрезков разбиениязначенияи(в случае непрерывной функцииони совпадают си, которые мы рассматривали выше, мы можем дать для разбиенияопределениенижней интегральной суммы: иверхней интегральной суммы: При измельчении разбиения, то есть при добавлении к множеству точек делениядополнительных точек отрезка, не совпадающих с уже имеющимися и рассмотрении новых, более мелких, отрезков деления, верхние интегральные суммы, очевидно, могут лишь уменьшиться, а нижние интегральные суммы -- лишь увеличиться: если-- разбиение с добавленными точками деления, то

Очевидно также, что для любого размеченного разбиения имеет место неравенствоОтсюда сразу следует такая теорема:

Пусть при существуют и равны друг другу пределы верхней и нижней интегральных сумм для функциина отрезке:

Тогда функция интегрируема на, причём Обратное утверждение:Пусть функция интегрируема на отрезке. Тогда пределы верхней и нижней интегральных сумм, составленных для этой функции на отрезке, существуют и равны определённому интегралу:

Доказательство. Как для верхней, так и для нижней интегральной суммы, соответствующей разбиению , можно указать такие точки разметки(при том же самом разбиении), что получающаяся интегральная сумма со значениями функции в этих точкахбудет произвольно мало отличаться от верхней (или нижней) интегральной суммы, а при достаточно мелком разбиении она мало отличается и от значения интеграла. Следовательно, как угодно мало (меньше, чем на) отличается от значения интеграла и верхняя (или нижняя) интегральная сумма; это говорит о том, что верхняя (нижняя) интегральная сумма стремится кпри неограниченном измельчении разбиения.Теорема 3.3   Если функция непрерывна на отрезке, то она интегрируема на этом отрезке, то есть существует число

        Доказательство.     Доказательство, по сути дела, было приведено выше, при построении интегральных сумм, соответствующих значениям и. Для строгости доказательства нужно лишь заметить, что при переходе ко всё более мелким разбиениям путём добавления новых точек делениянижние интегральные суммыне убывают и ограничены сверху значением любой из верхних интегральных сумм; аналогично, верхние интегральные суммыне возрастают при измельчении разбиения и ограничены снизу значением любой нижней интегральной суммы. Поэтому для доказательства существования предела достаточно теперь сослаться на теорему о существовании предела монотонной ограниченной функции. Проверим, что данное определение площади криволинейной трапеции не противоречит формуле, задающей площадь обычной трапеции. Обычная трапеция получается, если функция-- линейна:. Это непрерывная на любом отрезкефункция, так что интеграл, задающий площадьпод графиком, существует:

Возьмём следующее размеченное разбиение с произвольно малым диаметром. Разобьём отрезок наравных частей, длина каждой из которых будет, а в качестве точек разметки возьмём середину соответствующего отрезка, то есть положим. тогда величинабудетв точности равна площади (см. рис.):

Значит, соответствующая этому размеченному разбиению интегральная сумма будет в точности равна площади трапеции. Поскольку мы можем взять диаметр такого разбиения произвольно малым (увеличивая), то предел для произвольных разбиений не может давать иного, кроме, значения. Тем самым мы доказали корректность определения площади криволинейной трапеции