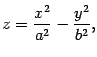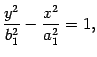- •2. Интегрирование подведением под знак дифференциала (см. Выше) и по частям. Интегралы, не берущиеся в элементарных функциях. (см. Выше)
- •4. Основные типы интегралов от элементарных дробей.
- •5. Интегралы, приводящиеся к интегралам от рациональных дробей, биноминальный дифференциал и подстановки Чебышева.
- •8. Суммы Дарбу и условия существования определенного интеграла.
- •9. Классы интегрируемых функций. Свойства определенных интегралов. Теоремы «о среднем».
- •11. Замена переменной в определенном интеграле, интегрирование по частям.
- •12. Площадь плоской фигуры и длина кривой в декартовых и полярных координатах, а также при параметрическом задании уравнений кривых.
- •13. Объем тела. Объем тела вращения и длина кривой в декартовых и полярных координатах и параметрически(см. Выше).
- •15. Несобственные интеграды. Интегралы с бесконечными пределами. Сходимость интеграла от неотрицательной функции. Признаки сходимости
- •16. Признаки сходиомсти несобственных интегралов. (см. Выше). 1-й и 2-й признаки сравнения интегралов. Абсолютная сходимость.
- •18. Признаки сходимости несобчтвенных интегралов от неограниченных фенкций. Признаки сравнения. См. Выше.
- •19. Определение линейного пространства. Элементы линейного пространства (вектора). Линейная зависимость и независимость между элементами. Базис и координаты.
- •20. Линейное пространство (см. Выше). Базис и координаты. (см. Выше). Размерность пространства (см. Выше).
- •21. Матрица и определители n-го порядка. Алгебраически едополнения и миноры.
- •22. Ранг матрицы. Теорема о базисном миноре и ее следствия. Методы вычисления ранга матрицы.
- •23. Система линейных кравнений. Решения системы однородных уравнений.
- •24. Неоднорродная система и ее совместность. Теорема Кронекера-Капелли.
- •25. Матричная алгебра. Сложение матриц и умножение матрицы на число. Перемножение матриц. Диагональная и единичная матрицы. Обратная матрица.
- •Умножение матриц Определение 14.4 Произведением матрицы размеровна матрицуразмеровназывается матрицаразмеров, элементы которой вычисляются по формуле
- •26. Матричная запись системы линейных уравнений (см. В 23). Решение систем в матричной форме (см. В 23)
- •27. Метод Гаусса решения системы линейных уравнений. (см. В 3)
- •28. Свойства определителей порядка n. Приведение определителя к треугольной и диагональной форме.
- •29. Элементарные преобразования матриц. Методы вычисления ранга матрицы (см. 22)
26. Матричная запись системы линейных уравнений (см. В 23). Решение систем в матричной форме (см. В 23)
27. Метод Гаусса решения системы линейных уравнений. (см. В 3)
28. Свойства определителей порядка n. Приведение определителя к треугольной и диагональной форме.
1.
При транспонировании матрицы определитель
не меняется, то есть
![]() .
2. Определитель произведения квадратных
матриц равен произведению определителей
сомножителей, то есть
.
2. Определитель произведения квадратных
матриц равен произведению определителей
сомножителей, то есть![]() .3.
Если в матрице
.3.
Если в матрице
![]() поменять
местами две строки, то ее определитель
сменит знак.4.
Если матрица
поменять
местами две строки, то ее определитель
сменит знак.4.
Если матрица
![]() имеет
две одинаковые строки, то ее определитель
равен нулю.5.
Если строку
матрицы умножить на число
имеет
две одинаковые строки, то ее определитель
равен нулю.5.
Если строку
матрицы умножить на число
![]() ,
то ее определитель умножится на это
число.6. Если
матрица содержит нулевую строку, то ее
определитель равен нулю.
7. Если одна
из строк матрицы равна другой, умноженной
на число
,
то ее определитель умножится на это
число.6. Если
матрица содержит нулевую строку, то ее
определитель равен нулю.
7. Если одна
из строк матрицы равна другой, умноженной
на число
![]() (строки
пропорциональны), то определитель
матрицы равен нулю.8.
Пусть в
матрице
(строки
пропорциональны), то определитель
матрицы равен нулю.8.
Пусть в
матрице
![]()
![]() -ая
строка имеет вид
-ая
строка имеет вид![]() .
Тогда
.
Тогда![]() ,
где матрица
,
где матрица![]() получается
из матрицы
получается
из матрицы![]() заменой
заменой![]() -ой
строки на строку
-ой
строки на строку![]() ,
а матрица
,
а матрица![]() --
заменой
--
заменой![]() -ой
строки на строку
-ой
строки на строку![]() .9. Если
к одной из строк матрицы добавить другую,
умноженную на число, то определитель
матрицы не изменится. 10.
Если одна
из строк матрицы является линейной
комбинацией других ее строк, то
определитель матрицы равен нулю.
.9. Если
к одной из строк матрицы добавить другую,
умноженную на число, то определитель
матрицы не изменится. 10.
Если одна
из строк матрицы является линейной
комбинацией других ее строк, то
определитель матрицы равен нулю.
Алгоритм
создания нулей в столбце.
Пусть требуется вычислить определитель
матрицы
![]() порядка
порядка![]() .
Если
.
Если![]() ,
то поменяем местами первую строку и
любую другую, в которой первый элемент
не нуль. В результате определитель
,
то поменяем местами первую строку и
любую другую, в которой первый элемент
не нуль. В результате определитель![]() ,
будет равен определителю новой матрицы
с противоположным знаком. Если же первый
элемент каждой строки равен нулю, то
матрица
,
будет равен определителю новой матрицы
с противоположным знаком. Если же первый
элемент каждой строки равен нулю, то
матрица![]() имеет
нулевой столбец и ее определитель равен
нулю. Итак, считаем, что уже в исходной
матрице
имеет
нулевой столбец и ее определитель равен
нулю. Итак, считаем, что уже в исходной
матрице![]() .
Первую строку оставляем без изменений.
Прибавим ко второй строке первую строку,
умноженную на число
.
Первую строку оставляем без изменений.
Прибавим ко второй строке первую строку,
умноженную на число![]() .
Тогда первый элемент второй строки
будет равен
.
Тогда первый элемент второй строки
будет равен![]() Остальные
элементы новой второй строки обозначим
Остальные
элементы новой второй строки обозначим![]() ,
,![]() .
Определитель новой матрицы равен
.
Определитель новой матрицы равен![]() .
Первую строку умножим на число
.
Первую строку умножим на число![]() и
прибавим к третьей. Первый элемент новой
третьей строки будет равен
и
прибавим к третьей. Первый элемент новой
третьей строки будет равен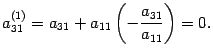 Остальные
элементы новой третьей строки обозначим
Остальные
элементы новой третьей строки обозначим![]() ,
,![]() .
Определитель новой матрицы равен
.
Определитель новой матрицы равен![]() .
Процесс получения нулей вместо первых
элементов строк продолжим дальше.
Наконец, первую строку умножим на число
.
Процесс получения нулей вместо первых
элементов строк продолжим дальше.
Наконец, первую строку умножим на число![]() и
прибавим к последней строке. В результате
получается матрица, обозначим ее
и
прибавим к последней строке. В результате
получается матрица, обозначим ее![]() ,
которая имеет вид
,
которая имеет вид
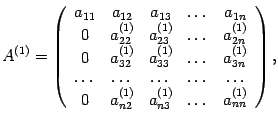 причем
причем
![]() .
Для вычисления определителя матрицы
.
Для вычисления определителя матрицы![]() используем
разложение по первому столбцу
используем
разложение по первому столбцу![]() Так
как
Так
как![]() ,
то
,
то
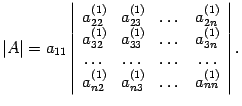 В
правой части стоит определитель матрицы
порядка
В
правой части стоит определитель матрицы
порядка
![]() .
К нему применим тот же алгоритм, и
вычисление определителя матрицы
.
К нему применим тот же алгоритм, и
вычисление определителя матрицы![]() сведется
к вычислению определителя матрицы
порядка
сведется
к вычислению определителя матрицы
порядка![]() .
Процесс повторяем до тех пор, пока не
дойдем до определителя второго порядка,
который вычисляется по определению.
.
Процесс повторяем до тех пор, пока не
дойдем до определителя второго порядка,
который вычисляется по определению.
29. Элементарные преобразования матриц. Методы вычисления ранга матрицы (см. 22)
- перестановка двух строк или двух столбцов;
- умножение всех элементов строки или столбца на любое число, отличное от нуля;
- прибавление ко всем элементам строки или столбца соответствующих элементов другой строки или другого столбца, умноженных на одно и то же число.
Элементарные преобразования не меняют ранга матрицы. Иногда к элементарным операциям относят и операцию транспонирования - замена каждой строки столбцом с тем же номером.
30-38. поверхности и их координаты
Сферой называется геометрическое место точек пространства, равноудаленных от фиксированной точки, называемой центром.
Сфера
радиуса
![]() с
центром в точке
с
центром в точке![]() имеет
уравнение
имеет
уравнение
|
|
|
В сферических координатах – p(ро) = R |
Для
ее изображения нарисуем сечения сферы
плоскостями, проходящими через центр
и параллельными координатным плоскостям.
Каждое такое сечение будет окружностью
радиуса 2 с центром в точке
![]() .
.

Эллипсоидом называется поверхность, каноническое уравнение которой имеет вид
|
|
(13.3) |
где
![]() ,
,![]() ,
,![]() --
положительные числа. Исследуем форму
эллипсоида. Из уравнения (13.3)
видно, что координаты точек поверхности
ограничены:
--
положительные числа. Исследуем форму
эллипсоида. Из уравнения (13.3)
видно, что координаты точек поверхности
ограничены:
![]() ,
,![]() ,
,![]() .
Эллипсоид обладает тремя плоскостями
симметрии, тремя осями симметрии и
центром симметрии. Ими служат соответственно
координатные плоскости, координатные
оси и начало координат. Для выяснения
формы эллипсоида рассмотрим его сечения
плоскостями. Найдем линию пересечения
эллипсоида с плоскостью
.
Эллипсоид обладает тремя плоскостями
симметрии, тремя осями симметрии и
центром симметрии. Ими служат соответственно
координатные плоскости, координатные
оси и начало координат. Для выяснения
формы эллипсоида рассмотрим его сечения
плоскостями. Найдем линию пересечения
эллипсоида с плоскостью![]() .
Так как любая точка плоскости
.
Так как любая точка плоскости![]() имеет
нулевую третью координату,
имеет
нулевую третью координату,![]() ,
то координаты точек эллипсоида на
плоскости
,
то координаты точек эллипсоида на
плоскости![]() удовлетворяют
уравнению
удовлетворяют
уравнению
|
|
(13.4) |
Получаем,
что линия пересечения является эллипсом
с полуосями
![]() и
и![]() .
А
.
А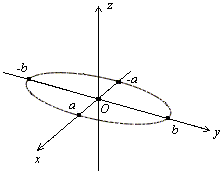 налогично,
сечение в плоскости
налогично,
сечение в плоскости![]() дает
эллипс
дает
эллипс
![]() с
полуосями
с
полуосями
![]() и
и![]() ,
а сечение плоскостью
,
а сечение плоскостью![]() --
эллипс
--
эллипс
![]()
с
полуосями
![]() и
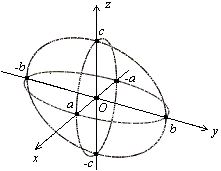
и![]() Нарисованный "каркас" из сечений
уже дает представление об эллипсоиде.
Но чтобы выяснить, как ведет себя
поверхность между нарисованными кривыми,
рассмотрим сечение эллипсоида плоскостью
Нарисованный "каркас" из сечений
уже дает представление об эллипсоиде.
Но чтобы выяснить, как ведет себя
поверхность между нарисованными кривыми,
рассмотрим сечение эллипсоида плоскостью![]() .
Эта плоскость параллельна плоскости
.
Эта плоскость параллельна плоскости![]() и
пересекает ось
и
пересекает ось![]() в
точке
в
точке![]() .
Уравнения этой линии
.
Уравнения этой линии Очевидно,
что если
Очевидно,
что если![]() ,
то ни одна точка пространства не может
удовлетворять этой системе: в левой
части первого уравнения стоит
неотрицательное число, а в правой --
отрицательное. Если
,
то ни одна точка пространства не может
удовлетворять этой системе: в левой
части первого уравнения стоит
неотрицательное число, а в правой --
отрицательное. Если![]() ,
то сечении получим лишь одну точку
,
то сечении получим лишь одну точку![]() или
или![]() в
зависимости от знака
в
зависимости от знака![]() .
Пусть
.
Пусть![]() .
Тогда первое уравнение преобразуем к
виду
.
Тогда первое уравнение преобразуем к
виду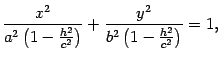 то
есть к виду
то
есть к виду
|
|
(13.5) |
г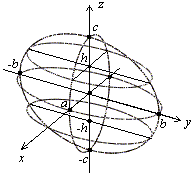 де
де![]() ,
,![]() .
Уравнение (13.5)
является уравнением эллипса, подобного
эллипсу, задаваемому уравнением (13.4),
с коэффициентом подобия
.
Уравнение (13.5)
является уравнением эллипса, подобного
эллипсу, задаваемому уравнением (13.4),
с коэффициентом подобия
![]() и
полуосями
и
полуосями![]() и
и![]() .
Ясно, что сечение плоскостью
.
Ясно, что сечение плоскостью![]() является
таким же эллипсом, расположенным
симметрично первому относительно
плоскости
является
таким же эллипсом, расположенным
симметрично первому относительно
плоскости![]() .
Нарисуем эти сечения . Таким образом,
весь эллипсоид составлен из эллипсов,
лежащих в плоскостях, параллельных
плоскости
.
Нарисуем эти сечения . Таким образом,
весь эллипсоид составлен из эллипсов,
лежащих в плоскостях, параллельных
плоскости![]() и
подобных эллипсу в плоскости
и
подобных эллипсу в плоскости![]() .
Так же, как для эллипса, точки пересечения
эллипсоида с координатными осями
называются вершинами эллипсоида, центр
симметрии -- центром эллипсоида. Числа
.
Так же, как для эллипса, точки пересечения
эллипсоида с координатными осями
называются вершинами эллипсоида, центр
симметрии -- центром эллипсоида. Числа![]() ,
,![]() ,
,![]() называются
полуосями. Если полуоси попарно различны,
то эллипсоид называетсятрехосным.
Если две полуоси равны друг другу, то
эллипсоид называется эллипсоидом
вращения.
Эллипсоид вращения может быть получен
вращением эллипса вокруг одной из осей.
Например, если
называются
полуосями. Если полуоси попарно различны,
то эллипсоид называетсятрехосным.
Если две полуоси равны друг другу, то
эллипсоид называется эллипсоидом
вращения.
Эллипсоид вращения может быть получен
вращением эллипса вокруг одной из осей.
Например, если
![]() ,
то все сечения эллипсоида плоскостями
,
то все сечения эллипсоида плоскостями![]() ,
,![]() ,
будут окружностями. Сам эллипсоид может
быть получен из эллипса
,
будут окружностями. Сам эллипсоид может
быть получен из эллипса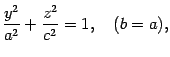 лежащего
в плоскости
лежащего
в плоскости![]() ,
при вращении его вокруг оси
,
при вращении его вокруг оси![]() .
.
Однополостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид
|
|
(13.6) |
где
![]() ,
,![]() ,
,![]() --
положительные числа. Исследуем форму
однополостного гиперболоида. Так же,
как эллипсоид, он имеет три плоскости
симметрии, три оси симметрии и центр
симметрии. Ими являются соответственно
координатные плоскости, координатные
оси и начало координат. Для построения
гиперболоида найдем его сечения
различными плоскостями. Найдем линию
пересечения с плоскостью
--
положительные числа. Исследуем форму
однополостного гиперболоида. Так же,
как эллипсоид, он имеет три плоскости
симметрии, три оси симметрии и центр
симметрии. Ими являются соответственно
координатные плоскости, координатные
оси и начало координат. Для построения
гиперболоида найдем его сечения
различными плоскостями. Найдем линию
пересечения с плоскостью![]() .
На этой плоскости
.
На этой плоскости![]() ,
поэтому
,
поэтому![]() Это
уравнение на плоскости
Это
уравнение на плоскости![]() задает
эллипс с полуосями
задает
эллипс с полуосями![]() и
и![]() .
Найдем линию пересечения с плоскостью
.
Найдем линию пересечения с плоскостью![]() .
На этой плоскости
.
На этой плоскости![]() ,
поэтому
,
поэтому
![]()
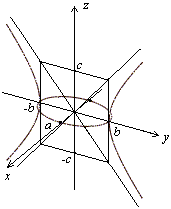 Это
уравнение гиперболы на плоскости
Это
уравнение гиперболы на плоскости
![]() ,
где действительная полуось равна
,
где действительная полуось равна![]() ,
а мнимая полуось равна
,
а мнимая полуось равна![]() .
Построим эту гиперболу. Сечение плоскостью
.
Построим эту гиперболу. Сечение плоскостью![]() также
является гиперболой с уравнением
также
является гиперболой с уравнением![]() Найдем
линии пересечения поверхности с
плоскостями
Найдем
линии пересечения поверхности с
плоскостями![]() ,
,![]() .
Уравнения этих линий
.
Уравнения этих линий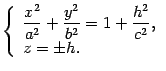 Первое
уравнение преобразуем к виду
Первое
уравнение преобразуем к виду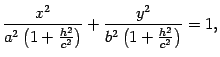 то
есть к виду
то
есть к виду
|
|
(13.7) |
где
![]() ,
,![]() .
Уравнение (13.7)
является уравнением эллипса, подобного
эллипсу в плоскости
.
Уравнение (13.7)
является уравнением эллипса, подобного
эллипсу в плоскости
![]() ,
с коэффициентом подобия
,
с коэффициентом подобия![]() и
полуосями
и
полуосями![]() и
и![]() .
Нарисуем полученные сечения .
.
Нарисуем полученные сечения .
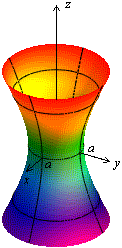
Е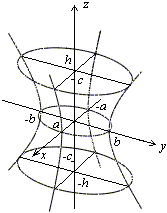 сли
в уравнении (13.6)
сли
в уравнении (13.6)
![]() ,
то сечения гиперболоида плоскостями,
параллельными плоскости
,
то сечения гиперболоида плоскостями,
параллельными плоскости![]() ,
являются окружностями. В этом случае
поверхность называетсяоднополостным
гиперболоидом вращения
и может быть получена вращением гиперболы,
лежащей в плоскости
,
являются окружностями. В этом случае
поверхность называетсяоднополостным
гиперболоидом вращения
и может быть получена вращением гиперболы,
лежащей в плоскости
![]() ,
вокруг оси
,
вокруг оси![]()
Двуполостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид
|
|
(13.8) |
где
![]() ,
,![]() ,
,![]() --
положительные числа. Исследуем форму
двуполостного гиперболоида. Так же, как
эллипсоид и однополостный гиперболоид,
он имеет три плоскости симметрии, три
оси симметрии и центр симметрии. Ими
являются соответственно координатные
плоскости, координатные оси и начало
координат. Для построения гиперболоида
найдем его сечения различными плоскостями.
Найдем линию пересечения с плоскостью
--
положительные числа. Исследуем форму
двуполостного гиперболоида. Так же, как
эллипсоид и однополостный гиперболоид,
он имеет три плоскости симметрии, три
оси симметрии и центр симметрии. Ими
являются соответственно координатные
плоскости, координатные оси и начало
координат. Для построения гиперболоида
найдем его сечения различными плоскостями.
Найдем линию пересечения с плоскостью![]() .
На этой плоскости
.
На этой плоскости![]() ,
поэтому
,
поэтому
![]() Координаты
ни одной точки плоскости
Координаты
ни одной точки плоскости
![]() не
могут удовлетворять данному уравнению.
Следовательно, двуполостный гиперболоид
не пересекает эту плоскость. Найдем
линию пересечения с плоскостью
не
могут удовлетворять данному уравнению.
Следовательно, двуполостный гиперболоид
не пересекает эту плоскость. Найдем
линию пересечения с плоскостью![]() .
На этой плоскости
.
На этой плоскости![]() ,
поэтому
,
поэтому![]()
Это
уравнение гиперболы на плоскости
![]() ,
где действительная полуось равна
,
где действительная полуось равна![]() ,
а мнимая полуось равна
,
а мнимая полуось равна![]() .
Построим эту гиперболу
.
Построим эту гиперболу
С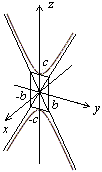 ечение
плоскостью
ечение
плоскостью![]() также
является гиперболой, с уравнением
также
является гиперболой, с уравнением
![]() Найдем
линии пересечения поверхности с
плоскостями
Найдем
линии пересечения поверхности с
плоскостями
![]() ,
,![]() .
Уравнения этих линий
.
Уравнения этих линий
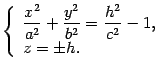 Очевидно,
что ни одна точка не может удовлетворять
этим уравнениям, если
Очевидно,
что ни одна точка не может удовлетворять
этим уравнениям, если
![]() .
Если
.
Если![]() или
или![]() ,
то плоскость имеет с исследуемой
поверхностью только одну точку
,
то плоскость имеет с исследуемой
поверхностью только одну точку![]() или
или![]() .
Эти точки называютсявершинами
гиперболоида. Пусть
.
Эти точки называютсявершинами
гиперболоида. Пусть
![]() .
Первое уравнение преобразуем к виду
.
Первое уравнение преобразуем к виду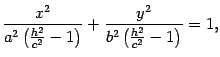 то
есть к виду
то
есть к виду
|
|
(13.9) |
где
![]() ,
,![]() .
Уравнение (13.9)
является уравнением эллипса, подобного
эллипсу в плоскости
.
Уравнение (13.9)
является уравнением эллипса, подобного
эллипсу в плоскости
![]() ,
с коэффициентом подобия
,
с коэффициентом подобия![]() и
полуосями
и
полуосями![]() и
и![]() .
Нарисуем полученные сечения .
.
Нарисуем полученные сечения .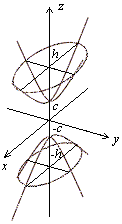 Если
в уравнении (13.8)
Если
в уравнении (13.8)
![]() ,
то сечения гиперболоида плоскостями,
параллельными плоскости
,
то сечения гиперболоида плоскостями,
параллельными плоскости![]() ,
являются окружностями. В этом случае
поверхность называетсядвуполостным
гиперболоидом вращения
и может быть получена вращением гиперболы,
лежащей в плоскости
,
являются окружностями. В этом случае
поверхность называетсядвуполостным
гиперболоидом вращения
и может быть получена вращением гиперболы,
лежащей в плоскости
![]() ,
вокруг оси
,
вокруг оси![]() .
.
Конусом второго порядка называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
|
|
(13.10) |
где
![]() ,
,![]() ,
,![]() --
положительные числа.
--
положительные числа.
Замечание 13.1 С математической точки зрения поверхность (13.10) лучше определять с помощью уравнения
|
|
(13.11) |
так
как в нем меньше параметров, но при этом,
во-первых, теряется аналогия с уравнениями
предыдущих поверхностей, а во-вторых,
если считать, что величины
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() имеют
размерность длины, то в уравнении (13.11)
размерности правой и левой части не
согласуются. Исследуем форму конуса.
Так же, как эллипсоид и гиперболоиды,
он имеет три плоскости симметрии, три
оси симметрии и центр симметрии. Ими
являются соответственно координатные
плоскости, координатные оси и начало
координат. Для построения конуса найдем
его сечения различными плоскостями.
Найдем линию пересечения с плоскостью
имеют
размерность длины, то в уравнении (13.11)
размерности правой и левой части не
согласуются. Исследуем форму конуса.
Так же, как эллипсоид и гиперболоиды,
он имеет три плоскости симметрии, три
оси симметрии и центр симметрии. Ими
являются соответственно координатные
плоскости, координатные оси и начало
координат. Для построения конуса найдем
его сечения различными плоскостями.
Найдем линию пересечения с плоскостью
![]() .
На этой плоскости
.
На этой плоскости![]() ,
поэтому
,
поэтому![]() Координаты
только одной точки плоскости
Координаты
только одной точки плоскости![]() могут
удовлетворять данному уравнению, а
именно, начала координат. Найдем линию
пересечения с плоскостью
могут
удовлетворять данному уравнению, а
именно, начала координат. Найдем линию
пересечения с плоскостью![]() .
На этой плоскости
.
На этой плоскости![]() ,
поэтому
,
поэтому![]() Это
уравнение пары прямых
Это
уравнение пары прямых![]() на
плоскости
на
плоскости![]() .
Построим эти прямые. Сечение плоскостью
.
Построим эти прямые. Сечение плоскостью![]() также
является парой прямых с уравнением
также
является парой прямых с уравнением![]() .
Нарисуем и эти прямые.
.
Нарисуем и эти прямые.
Н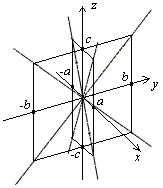 айдем
линии пересечения поверхности с
плоскостями
айдем
линии пересечения поверхности с
плоскостями![]() ,
,![]() .
Уравнения этих линий
.
Уравнения этих линий
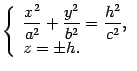 Первое
уравнение преобразуем к виду
Первое
уравнение преобразуем к виду
![]() то
есть к виду
то
есть к виду
|
|
(13.12) |
г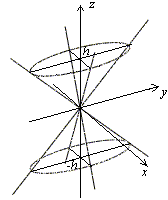 де
де![]() ,
,![]() .
Уравнение (13.12)
является уравнением эллипса. Нарисуем
полученные сечения. Точка пересечения
конуса с плоскостью
.
Уравнение (13.12)
является уравнением эллипса. Нарисуем
полученные сечения. Точка пересечения
конуса с плоскостью
![]() называетсявершиной
конуса. Если в уравнении (13.10)
называетсявершиной
конуса. Если в уравнении (13.10)
![]() ,
то сечения конуса плоскостями параллельными
плоскости
,
то сечения конуса плоскостями параллельными
плоскости![]() являются
окружностями. В этом случае поверхность
называетсяпрямым
круговым конусом
и может быть получена вращением прямой,
лежащей в плоскости
являются
окружностями. В этом случае поверхность
называетсяпрямым
круговым конусом
и может быть получена вращением прямой,
лежащей в плоскости
![]() ,
вокруг оси
,
вокруг оси![]() .
Именно с таким конусом мы имеем дело в
шкЭллиптическим
параболоидом
называется поверхность, уравнение
которой в некоторой декартовой системе
координат имеет вид
.
Именно с таким конусом мы имеем дело в
шкЭллиптическим
параболоидом
называется поверхность, уравнение
которой в некоторой декартовой системе
координат имеет вид
|
|
(13.13) |
где
![]() и
и![]() --
положительные числа. Исследуем форму
эллиптического параболоида. Он имеет
две плоскости симметрии и ось симметрии.
Ими являются соответственно координатные
плоскости
--
положительные числа. Исследуем форму
эллиптического параболоида. Он имеет
две плоскости симметрии и ось симметрии.
Ими являются соответственно координатные
плоскости![]() ,
,![]() и
координатная ось
и
координатная ось![]() .
Для построения эллиптического параболоида
найдем его сечения различными плоскостями.
Найдем линию пересечения с плоскостью
.
Для построения эллиптического параболоида
найдем его сечения различными плоскостями.
Найдем линию пересечения с плоскостью![]() .
На этой плоскости
.
На этой плоскости![]() ,
поэтому
,
поэтому![]() Координаты
только одной точки плоскости
Координаты
только одной точки плоскости![]() могут
удовлетворять данному уравнению, а
именно, начала координат. Найдем линию
пересечения с плоскостью
могут
удовлетворять данному уравнению, а
именно, начала координат. Найдем линию
пересечения с плоскостью![]() .
На этой плоскости
.
На этой плоскости![]() ,
поэтому
,
поэтому![]() Это уравнение параболы на плоскости
Сечение плоскостью
Это уравнение параболы на плоскости
Сечение плоскостью![]() также
является параболой. Найдем линии
пересечения поверхности с плоскостью
также
является параболой. Найдем линии
пересечения поверхности с плоскостью![]() .
Уравнения этой линии
.
Уравнения этой линии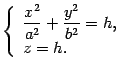 Очевидно,
что только одна точка (начало координат)
удовлетворяет этим уравнениям, если
Очевидно,
что только одна точка (начало координат)
удовлетворяет этим уравнениям, если![]() .
Эта точка называетсявершиной
параболоида. Пусть
.
Эта точка называетсявершиной
параболоида. Пусть
![]() .
Первое уравнение преобразуем к виду
.
Первое уравнение преобразуем к виду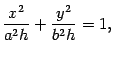 то
есть к виду
то
есть к виду
|
|
(13.14) |
где
![]() ,
,![]() .
Уравнение (13.14)
является уравнением эллипса. Нарисуем
полученное сечение (рис. 13.19). При
.
Уравнение (13.14)
является уравнением эллипса. Нарисуем
полученное сечение (рис. 13.19). При
![]() плоскость
поверхность не пересекает.
плоскость
поверхность не пересекает.
Р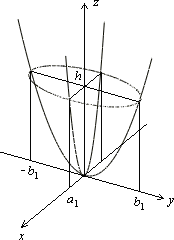 ис.13.19.Сечения
эллиптического параболоида координатными
плоскостям.
ис.13.19.Сечения
эллиптического параболоида координатными
плоскостям.
Найдем
сечения параболоида плоскостями
![]() ,
параллельными плоскости
,
параллельными плоскости![]() .
Линии этих сечений удовлетворяют
уравнениям
.
Линии этих сечений удовлетворяют
уравнениям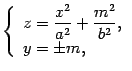 и
являются параболами, такими же, как в
плоскости
и
являются параболами, такими же, как в
плоскости![]() ,
только сдвинутыми вверх на величину
,
только сдвинутыми вверх на величину![]() ,
их вершины при таком сдвиге лежат на
параболе, получившейся в сечении
плоскостью
,
их вершины при таком сдвиге лежат на
параболе, получившейся в сечении
плоскостью![]() .
.
С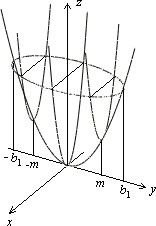 ледовательно,
вся поверхность может быть получена
движением параболы, лежащей в плоскости
ледовательно,
вся поверхность может быть получена
движением параболы, лежащей в плоскости![]() .
Парабола должна двигаться так, чтобы
ее плоскость была параллельна плоскости
.
Парабола должна двигаться так, чтобы
ее плоскость была параллельна плоскости![]() ,
а вершина скользила по параболе в
плоскости
,
а вершина скользила по параболе в
плоскости![]() .
Если в уравнении (13.13)
.
Если в уравнении (13.13)
![]() ,
то сечения плоскостями, параллельными
плоскости
,
то сечения плоскостями, параллельными
плоскости![]() ,
являются окружностями. В этом случае
поверхность называетсяпараболоидом
вращения и
может быть образована вращением параболы,
лежащей в плоскости
,
являются окружностями. В этом случае
поверхность называетсяпараболоидом
вращения и
может быть образована вращением параболы,
лежащей в плоскости
![]() ,
вокруг оси
,
вокруг оси![]() .
.
Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
|
|
(13.15) |
где
![]() и
и![]() --
положительные числа. Исследуем форму
гиперболического параболоида. Так же,
как и эллиптический параболоид, он имеет
две плоскости симметрии и ось симметрии.
Ими являются соответственно координатные
плоскости
--
положительные числа. Исследуем форму
гиперболического параболоида. Так же,
как и эллиптический параболоид, он имеет
две плоскости симметрии и ось симметрии.
Ими являются соответственно координатные
плоскости![]() ,
,![]() и
координатная ось
и
координатная ось![]() .
Для построения гиперболического
параболоида найдем его сечения различными
плоскостями. Найдем линию пересечения
с плоскостью
.
Для построения гиперболического
параболоида найдем его сечения различными
плоскостями. Найдем линию пересечения
с плоскостью![]() .
На этой плоскости
.
На этой плоскости![]() ,
поэтому
,
поэтому
![]() Это
уравнение определяет на плоскости
Это
уравнение определяет на плоскости
![]() пару
прямых
пару
прямых![]() .
Найдем линию пересечения с плоскостью
.
Найдем линию пересечения с плоскостью![]() .
На этой плоскости
.
На этой плоскости![]() ,
поэтому
,
поэтому![]() Это
уравнение на плоскости
Это
уравнение на плоскости![]() задает
параболу, ветви которой направлены
вниз. Построим ее. Сечение плоскостью
задает
параболу, ветви которой направлены
вниз. Построим ее. Сечение плоскостью![]() также
является параболой
также
является параболой![]() но
ее ветви направлены вверх. Нарисуем и
ее.
но
ее ветви направлены вверх. Нарисуем и
ее.
Н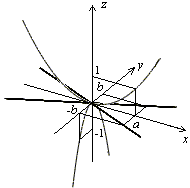 айдем
линии пересечения поверхности с
плоскостью
айдем
линии пересечения поверхности с
плоскостью![]() ,
,![]() .
Уравнения этой линии
.
Уравнения этой линии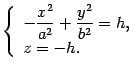 Первое
уравнение преобразуем к виду
Первое
уравнение преобразуем к виду![]() то
есть к виду
то
есть к виду
|
|
(13.16) |
где
![]() ,
,![]() .
Уравнение (13.16)
является уравнением гиперболы. Ее
действительная ось параллельна оси
.
Уравнение (13.16)
является уравнением гиперболы. Ее
действительная ось параллельна оси
![]() ,
а мнимая -- оси
,
а мнимая -- оси![]() .
Полуоси равны соответственно
.
Полуоси равны соответственно![]() и
и![]() .
Найдем линии пересечения с плоскостями
.
Найдем линии пересечения с плоскостями![]() ,
параллельными плоскости
,
параллельными плоскости![]() .
Уравнения этих линий
.
Уравнения этих линий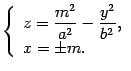 Первое
из этих уравнений является уравнением
параболы, такой же, как и в сечении
плоскостью
Первое
из этих уравнений является уравнением
параболы, такой же, как и в сечении
плоскостью![]() ,
только сдвинутой вдоль оси
,
только сдвинутой вдоль оси![]() на
величину
на
величину![]() вверх.
Эти параболы изображены на рисунке.
вверх.
Эти параболы изображены на рисунке.
Т ак
как
ак
как![]() --
произвольное число, то вся поверхность
может быть получена движением параболы,
лежащей в плоскости
--
произвольное число, то вся поверхность
может быть получена движением параболы,
лежащей в плоскости![]() .
Передвигать параболу нужно так, чтобы
ее плоскость оставалась параллельной
плоскости
.
Передвигать параболу нужно так, чтобы
ее плоскость оставалась параллельной
плоскости![]() ,
а вершина скользила по параболе в
плоскости
,
а вершина скользила по параболе в
плоскости![]() .
Плоскость
.
Плоскость![]() ,
,![]() ,
пересекает поверхность по гиперболе,
но в отличие от гиперболы (13.16),
ее действительная ось параллельна
теперь оси
,
пересекает поверхность по гиперболе,
но в отличие от гиперболы (13.16),
ее действительная ось параллельна
теперь оси
![]() ,
а мнимая -- оси
,
а мнимая -- оси![]() .
.
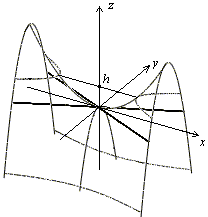
Рис.13.25.Дополнительное сечение
Цилиндрической поверхностью называется геометрическое место параллельных прямых, пересекающих данную линию. Эта линия называется направляющей, а параллельные прямые -- образующими. Рассмотрим уравнение вида
|
|
(13.17) |
и
покажем, что оно определяет цилиндрическую
поверхность с образующими, параллельными
оси
![]() .
Пусть
.
Пусть![]() --
некоторая точка, координаты которой
удовлетворяют уравнению (13.17).
Поскольку в это уравнение не входит
явно переменная
--
некоторая точка, координаты которой
удовлетворяют уравнению (13.17).
Поскольку в это уравнение не входит
явно переменная
![]() ,
ему будут удовлетворять координаты
всех точек
,
ему будут удовлетворять координаты
всех точек![]() ,
где
,
где![]() --
любое число. Следовательно, при любом
--
любое число. Следовательно, при любом![]() точка
точка![]() лежит
на поверхности, определяемой
уравнением (13.17).
Отсюда следует, что на поверхности
целиком лежит прямая, проходящая через
точку
лежит
на поверхности, определяемой
уравнением (13.17).
Отсюда следует, что на поверхности
целиком лежит прямая, проходящая через
точку
![]() параллельно
оси
параллельно
оси![]() .
А это означает, что поверхность,
определяемая уравнением (13.17),
составлена из прямых, параллельных оси
.
А это означает, что поверхность,
определяемая уравнением (13.17),
составлена из прямых, параллельных оси
![]() ,
то есть она является цилиндрической
поверхностью. Заметим, что на плоскости
,
то есть она является цилиндрической
поверхностью. Заметим, что на плоскости![]() уравнение (13.17)
определяет направляющую рассматриваемой
цилиндрической поверхности. Итак, делаем
вывод, что если уравнение поверхности
не содержит в явном виде какой-либо
переменной, то это уравнение определяет
в пространстве цилиндрическую поверхность
с образующими, параллельными оси
отсутствующего переменного и направляющей,
которая в плоскости двух других переменных
имеет то же самое уравнение.
уравнение (13.17)
определяет направляющую рассматриваемой
цилиндрической поверхности. Итак, делаем
вывод, что если уравнение поверхности
не содержит в явном виде какой-либо
переменной, то это уравнение определяет
в пространстве цилиндрическую поверхность
с образующими, параллельными оси
отсутствующего переменного и направляющей,
которая в плоскости двух других переменных
имеет то же самое уравнение.
Поверхность, которая в некоторой декартовой системе координат задается уравнением
|
|
(13.18) |
называется эллиптическим цилиндром, поверхность, которая задается уравнением
|
|
(13.19) |
называется гиперболическим цилиндром, а которая задается уравнением
|
|
(13.20) |
н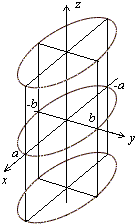 азываетсяпараболическим
цилиндром.
Для того чтобы построить поверхность,
задаваемую уравнением (13.18),
или уравнением (13.19),
или (13.20),
достаточно нарисовать на плоскости
азываетсяпараболическим
цилиндром.
Для того чтобы построить поверхность,
задаваемую уравнением (13.18),
или уравнением (13.19),
или (13.20),
достаточно нарисовать на плоскости
![]() направляющую,
уравнение которой на этой плоскости
совпадает с уравнением самой поверхности,
и затем через точки направляющей провести
образующие параллельно оси
направляющую,
уравнение которой на этой плоскости
совпадает с уравнением самой поверхности,
и затем через точки направляющей провести
образующие параллельно оси![]() .
Для наглядности следует построить также
одно-два сечения плоскостями, параллельными
плоскости
.
Для наглядности следует построить также
одно-два сечения плоскостями, параллельными
плоскости![]() .
В каждом таком сечении получим такую
же кривую, как и исходная направляющая.
Изображения этих цилиндров сечениями
приведены на рисунках 13.27, 13.29 и 13.31, а их
объемные изображения -- на рисунках
13.28, 13.30 и 13.32.
.
В каждом таком сечении получим такую
же кривую, как и исходная направляющая.
Изображения этих цилиндров сечениями
приведены на рисунках 13.27, 13.29 и 13.31, а их
объемные изображения -- на рисунках
13.28, 13.30 и 13.32.
Изображение эллиптического цилиндра с помощью сечений
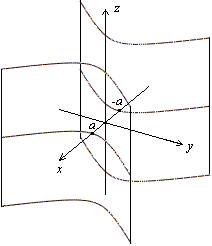
Изображение гипербоического цилиндра с помощью сечений
И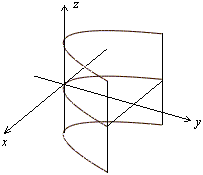 зображение
параболического цилиндра с помощью
сечений
зображение
параболического цилиндра с помощью
сечений