22. Плотность вероятности. Свойства плотности вероятности.

Плотностью вероятности непрерывной случайной величины Х называется производная ее функции распределения: .

Свойства:

1. Плотность вероятности – неотрицательная функция, т.е.

2. Вероятность попадания непрерывной случайной величины в интервал [a,b) равна определенному интегралу от ее плотности вероятности в пределах от a до b, т.е.: .

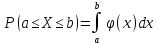3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле: .

4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице: .

22. Математическое ожидание дискретной и непрерывной случайной величины. Свойства математического ожидания.

Математическим ожиданием, или средним значением, М(Х) дискретной величины Х называется сумма произведений всех ее значений на соответствующие им вероятности.

Если дискретная случайная величина Х принимает бесконечное, но счетное множество значений ч, то математическим ожиданием называется сумма ряда:

Свойства:

1. Математическое ожидание постоянной величины равно самой постоянной: М(С)=С.

2. Постоянный множитель можно выносить за знак математического ожидания, т.е.: М(kX)=kM(X).

3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно такой же сумме их математических ожиданий, т.е.: M(X±Y)=M(X)±M(Y).

4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий: M(XY)=M(X)M(Y).

5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно 0: M[X-M(X)]=0.

22. Дисперсия случайной величины. Свойства дисперсии. Среднее квадратическое отклонение.

Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания: D(X)=M[X-M(X)]² или D(X)=M(X-a)^2.

Если случайная величина Х – дискретная с конечным числом значений, то .

Если случайная величина Х – дискретная с бесконечным, но счетным множеством значений, то .

Средним квадратичным отклонением случайной величины Х называется арифметическое значение корня квадратного из дисперсии: .

Свойства дисперсии:

1. Дисперсия постоянной величины равна 0: D(C)=0.

2. Постоянный множитель можно выносит за знак дисперсии, возведя его в квадрат: D(kX)=k²D(X).

3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания: D(X)=M(X²)-[M(X)]².

4. Дисперсия алгебраической суммы конечного числа независимых случайных величин равна сумме их дисперсий: D(X±Y)=D(X)+D(Y).

22. Основные законы распределения дискретных случайных величин (биномиальный, Пуассона, геометрический).

23. Основные законы распределения непрерывных случайных величин (равномерный, показательный, нормальный).

24. Неравенство Чебышева. Сходимость по вероятности.

25. Теорема Чебышева. Теорема Бернулли.

26. Центральная предельная теорема.