17. Размещения, сочетания, перестановки.

Правило суммы.

Если элемент А₁ может быть выбран n₁, элемент А₂ – другими n₂ способами, А₃ – отличными от первых двух n₃ способами и т.д., А_k – n_k способами отличных от первых (k-1), то выбор одного из элементов: или А₁, или А₂, …, или А_k может быть осуществлен n₁+n₂+…+n_k способами.

Правило произведения.

Если элемент А₁ может быть выбран n₁, после каждого такого выбора элемент А₂ – другими n₂ способами и т.д., после каждого (k-1) выбора элемент А_k может быть выбран n_k способами, то выбор одного всех элементов А₁, А₂, …, А_k в указанном порядке может быть осуществлен n₁n₂…n_k способами.

Пусть дано множество из n различных элементов, из него могут быть образованы множества из m элементов. (0≤m≤n).

Размещениями из n элементов по m называются комбинации, составленные из n элементов по m отличающиеся либо составом, либо порядком расположения.

Сочетаниями называются комбинации, составленные из n элементов по m, отличающиеся только составом элементов.

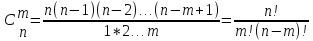
Перестановками называются комбинации, составленные из n элементов, отличающиеся только порядком расположения этих элементов.

P_n=n!

18. Условная вероятность. Теорема умножения вероятностей. Независимость событий.

Если к комплексу условий, при котором изучалась вероятность Р(В), добавить новее условие А, то полученная вероятность события В, найденная при условии, что событие А произошло, называется условной вероятностью события В и обозначается Р_А(В) или Р(В/А).

Теорема умножения вероятностей: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло.

Р(АВ)=Р(А)Р_А(В)=Р(В)Р_В(А).

Событие В называется независимым от события А, если его вероятность не меняется от того, произошло событие А или нет. Р_А(В)=P(В).

Зависимость и независимость событий всегда взаимны. Два события называются независимыми, если появление одного из них не меняет вероятности наступления другого.

19. Теорема сложения вероятностей.

А) Теорема. Вероятность суммы несовместных событий равна сумме вероятностей этих событий: Р(А+В+..+К)=Р(А)+Р(В)+…Р(К)

Следствие 1. Сумма вероятностей событий, образующих полную группу, равна единице: Р(А)+Р(В)+…Р(К)=1.

Следствие 2. Сумма вероятностей противоположных событий равна единице: Р(А)+Р( )=1

Б) (Для совместных событий) Теоремы. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения: Р(А+В)=Р(А)+Р(В)-Р(АВ).

В случае трех и более совместных событий переходим к противоположному событию L:

L=, т.е. вероятность суммы нескольких совместных событий равна разности между единицей и вероятностью произведения противоположных событий.

20. Формула полной вероятности. Формула Байеса.

Теорема. Если событие F может произойти только при условии появления одного из событий (гипотез) А₁,А₂,…А_n, образующих полную группу, то вероятность события F равна сумме произведений вероятностей каждого из этих событий на соответствующие условные вероятности события F:

Если событие F, которое может появиться только с одной из гипотез А₁,А₂,…А_n, произошло и необходимо произвести количественную переоценку априорных вероятностей этих гипотез Р(А₁), Р(А₂), … Р(А_n), известных до испытания, т.е. надо найти апостериорные условные вероятности гипотез Р_F(А₁), Р_F(А₂), … Р_F(А_n). Их можно найти с помощью формулы Байеса:

21. Схема повторных испытаний. Формула Бернулли.

Последовательность независимых испытаний называется схемой Бернули: если вероятность наступления события А в каждом испытании не меняется в зависимости от исходов других, то такие испытания называются независимыми относительно события А. Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события А в каждом испытании одна и также.

Теорема. Если вероятность р наступления события А в каждом испытании постоянна, то вероятность Р_m,n того, что событие А наступит m раз в n независимых испытаниях, равна: 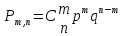, где q=1-p.

Число всех комбинаций равно . Вероятность каждой такой комбинации по теореме умножения для независимых событий равна . В связи с тем, что комбинации между собой несовместны, получим .

Число m₀ наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события Р_m,n по крайней мере не меньше вероятностей других событий Р_m,n при любом m.

np-q≤m₀≤np+q