
- •Числовые ряды. Определение сходящегося числового ряда. Геометрический ряд.
- •Свойства сходящихся рядов. Необходимый признак сходимости.
- •Теоремы сравнения (признаки сравнения).
- •Признаки сходимости Даламбера и Коши.
- •Интегральный признак сходимости. Сходимость обобщенного гармонического ряда.
- •Знакопеременные числовые ряды. Абсолютно и условно сходящиеся ряды. Признак Лейбница сходимости знакочередующегося ряда.
- •Функциональные ряды. Область сходимости. Сходимость ряда xn.
- •Равномерно сходящиеся последовательности и ряды. Признак Вейерштрасса равномерной сходимости функционального ряда.
- •Степенные ряды. Теорема Абеля. Радиус сходимости степенного ряда.
- •Выражения для радиуса сходимости степенного ряда через коэффициенты ряда. Как найти интервал сходимости степенного ряда?
- •Свойства степенных рядов.
- •Ряд Тейлора. Ряд Маклорена.
- •Разложение функций ex, sinx, cosx в ряд Тейлора.
- •Событие. Несовместные, равносильные, достоверные, невозможные, равновозможные и единственно возможные, противоположные события. Полная группа событий.
- •Классическое и статистическое определение вероятности.
- •Размещения, сочетания, перестановки.
- •Условная вероятность. Теорема умножения вероятностей. Независимость событий.
- •Теорема сложения вероятностей.
- •Формула полной вероятности. Формула Байеса.
- •Теорема Пуассона. Условие применимости формулы Пуассона для вычисления вероятности в схеме повторных испытаний.
- •Локальная и интегральная формулы Муавра-Лапласа. Условие их применимости для вычисления вероятности в схеме повторных испытаний.
- •Случайная величина. Дискретные и непрерывные случайные величины. Закон распределения случайной величины, ряд распределения. Независимость случайных величин.
- •Функция распределения случайной величины. Свойства функции распределения.
- •Плотность вероятности. Свойства плотности вероятности.
- •Математическое ожидание дискретной и непрерывной случайной величины. Свойства математического ожидания.
- •Дисперсия случайной величины. Свойства дисперсии. Среднее квадратическое отклонение.
ВОПРОСЫ (к зачету за 3-й сем) ПО КУРСУ
“ВЫСШАЯ МАТЕМАТИКА ”
Лектор С.Н. Чириков. Группы Д3-013,130
-
Числовые ряды. Определение сходящегося числового ряда. Геометрический ряд.
Числовой
ряд – бесконечная сумма членов бесконечной
числовой последовательности {Un}
называется числовым рядом: u1
+ u2+ u3
+ … + un+
… =

Частичные суммы ряда - Sn, они образуют последовательность {Sn} -последовательность частичных сумм (бесконечного) ряда un –общий член ряда.
S1=u1
S2=u1+u2
Sn=u1+u2+…+un+…
Ряд
называется сходящимся, если существует
конечный предел последовательности
его частичных сумм
 (сумма ряда)=
(сумма ряда)=
Если предел не существует или бесконечен, то последовательность называется расходящейся.
Геометрический ряд – это сумма всех членов геометрической последовательности с первым членом a и знаменателем q
 a0+a0q+a0q2+…+a0qn-1+…
a0+a0q+a0q2+…+a0qn-1+…
Sn=
 ,
при q≠1
,
при q≠1

-
Свойства сходящихся рядов. Необходимый признак сходимости.
-
Если ряд
 сходится и его сумма S, то ряд
сходится и его сумма S, то ряд
 тоже сходится и его сумма
тоже сходится и его сумма
 S.
S. -
Если ряды
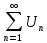 и
и
 - сходятся, и их суммы S1 и S2,
то ряд
- сходятся, и их суммы S1 и S2,
то ряд
 и его сумма равна S1±S2
и его сумма равна S1±S2 -
Добавлении (или отбрасывании) конечного числа членов не влияет на сходимость.
Пусть
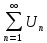 и
и
 ,
тогда начиная с нечетного номера N>ip
,
тогда начиная с нечетного номера N>ip

Необходимый признак ходимости ряда.
Если
ряд
 сходиться, то
сходиться, то
 .
.
Следствие:
Если
 ,
то ряд расходится.
,
то ряд расходится.
Замечание: Этот признак необходимый, но не достаточный.
-
Теоремы сравнения (признаки сравнения).
1-ый признак сравнения.
Пусть
даны
 и
и
 и для любого n Un≤Vn,
если ряд
и для любого n Un≤Vn,
если ряд
 сходится, то и ряд
сходится, то и ряд
 сходится, если
сходится, если
 расходится, то и
расходится, то и
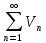 расходится. (данная теорема справедлива,
если неравенство выполнимо не для всех
n, а начиная с некоторого)
расходится. (данная теорема справедлива,
если неравенство выполнимо не для всех
n, а начиная с некоторого)
2-ой признак сравнения.
Если
для рядов
 и
и
 существует предел
существует предел
 ,
то оба ряда либо одновременно сходятся,
либо расходятся.
,
то оба ряда либо одновременно сходятся,
либо расходятся.
 - неизвестный ряд.
- неизвестный ряд.
 - ряд сравнения, чаще всего используются:
- ряд сравнения, чаще всего используются:
-
 - геометрический ряд:
- геометрический ряд:
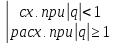
-
f

-
Признаки сходимости Даламбера и Коши.
Признак Д'Аламбера.
Если
для ряда
 существует конечный предел отношений
существует конечный предел отношений

Признак Коши.
Если
для ряда
 существует конечный предел отношений
существует конечный предел отношений

-
Интегральный признак сходимости. Сходимость обобщенного гармонического ряда.
Если
f(x) при х ≥1 непрерывна, положительна,
монотонно убывает и для всех хεnεN,
f(n)=Un, то ряд
 сходится или расходится одновременно
с несобственным интегралом
сходится или расходится одновременно
с несобственным интегралом
 .
Теорема справедлива в том случае, если
f(x) непрерывна, неотрицательна и монотонно
возрастает при х≥а (а>1), то ряд будет
сходиться или расходиться одновременно
с
.
Теорема справедлива в том случае, если
f(x) непрерывна, неотрицательна и монотонно
возрастает при х≥а (а>1), то ряд будет
сходиться или расходиться одновременно
с
 .
.

-
Знакопеременные числовые ряды. Абсолютно и условно сходящиеся ряды. Признак Лейбница сходимости знакочередующегося ряда.
 - произвольные знаки.
- произвольные знаки.
 - абсолютно сходится, если сходится ряд
составленный из модулей его членов
- абсолютно сходится, если сходится ряд
составленный из модулей его членов

 – условно сходится , если
– условно сходится , если
 - сходится, а ряд из модулей
- сходится, а ряд из модулей
 - расходится.
- расходится.
Ряд
вида
 ,
где все Un≥0 называется
знакочередующимся.
,
где все Un≥0 называется
знакочередующимся.
Признак
Лейбница: Если члены знакочередующегося
ряда убывают по абсолютной величине
U1>U2>U3>…>Un…
и
 ,
то знакочередующийся ряд сходится и
его сумма не превосходит первого члена
S≤U1
,
то знакочередующийся ряд сходится и
его сумма не превосходит первого члена
S≤U1
-
Функциональные ряды. Область сходимости. Сходимость ряда xn.
Функциональной
последовательностью называется
бесконечное, занумерованное множество
функций
Функция
F(x) называется пределом функциональной
последовательности
 на Х, если равенство F(x)=
на Х, если равенство F(x)= выполняется в каждой точке Х или,
если для любых хεХ и всех Ε>0 существует
N(E;x)
при n>N
|fn(x)-F(x)|<E.
выполняется в каждой точке Х или,
если для любых хεХ и всех Ε>0 существует
N(E;x)
при n>N
|fn(x)-F(x)|<E.
Ряд
вида
 (
( ),
где fn(x)
– члены функциональной последовательности,
называется функциональным рядом.
),
где fn(x)
– члены функциональной последовательности,
называется функциональным рядом.
При каждом фиксированном значении х=х0 этот функциональный ряд представляет собой обычный числовой ряд.
Если этот числовой ряд сходиться, то значение х0 – называют точкой сходимости функционального ряда. Совокупность всех точек сходимости называют областью сходимости ряда.
Энной частичной суммой функционального ряда называется функция вида: Sn(x)=f1(x)+f2(x)+..+ fn(x).
Суммой
функционального ряда называется функция
S(x)= ,
при условии, что этот придел существует
в каждой точке Х (области сходимости
функционального ряда). А сам ряд называется
сходящимся на Х. Область сходимости
функционального ряда может быть найдена
с помощью признака Д'Аламбера или Коши.
,
при условии, что этот придел существует
в каждой точке Х (области сходимости
функционального ряда). А сам ряд называется
сходящимся на Х. Область сходимости
функционального ряда может быть найдена
с помощью признака Д'Аламбера или Коши.

