Исследование системы на устойчивость Исследование системы на устойчивость методом Гурвица.
Для исследования системы на устойчивость методом Гурвица требуется составить матрицу Гурвица. Для этого определим коэффициенты характеристического уравнения:
Расчеты проведём, используя программный пакет MathCAD.
Определители диагональных миноров матрицы Гурвица больше нуля, следовательно, система устойчива.
Исследование системы на устойчивость методом Михайлова.
Требуется построить годограф Михайлова для замкнутой системы.
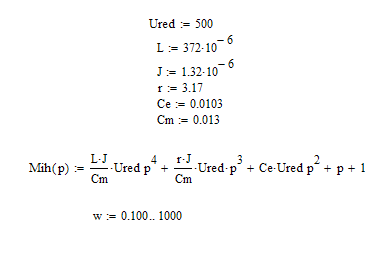
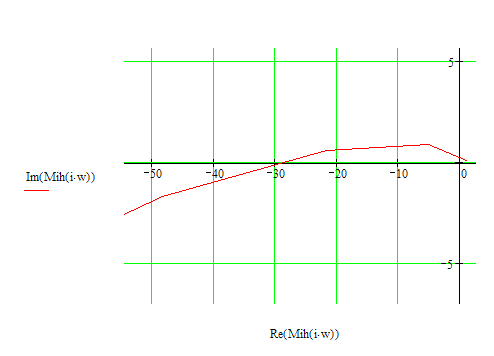
Рисунок 14. Годограф Михайлова замкнутой системы.
Годограф Михайлова разомкнутой системы располагается в трёх четвертях координатной плоскости. Так как характеристическое уравнение системы имеет третий порядок, можно сделать вывод о том, что система устойчива.
Исследование системы на устойчивость методом Найквиста.
Построим АФЧХ для разомкнутой системы.
Рисунок 15. АФЧХ разомкнутой системы.
АФЧХ замкнутой системы не охватывает точку с координатами (-1; 0) (см. рис. 15). Исходя из этого, можно сделать вывод о том, что система устойчива.
Система автоматического управления двумя приводами
В рамках данного курсового проекта было проведено исследование работы системы автоматического управления двумя приводами. Обе системы оснащены ПИД-регуляторами. Подбор коэффициентов ПИД-регуляторов будем осуществлять с помощью блока NCD OutPort.
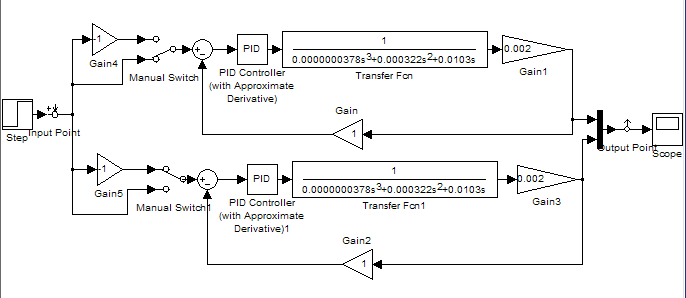
Рис. 16 Схема системы автоматического управления двумя приводами
График переходного процесса каждого двигателя.
Рис. 17 Реакция системы на единичное ступенчатое воздействие
Исследование системы с учетом нелинейности.
Любая механическая система обладает определённой нелинейностью, связанной с люфтом, проскальзыванием, характеристиками электродвигателя и другими факторами. В рассматриваемой системе автоматического управления учтем нелинейность люфт.
Рис. 18 Схема системы автоматического управления двумя приводами с учетом возмущающего воздействия и люфта.
Рис. 19 Реакция системы на единичное ступенчатое воздействие
Как мы видим наша система сохранила устойчивость при воздействии на нее возмущающего воздействия, люфта, но в результате у нас появилось ошибка, и увеличилось время переходного процесса.
Исследование системы на робастность
Робастность — это способность системы сохранять заданный запас устойчивости при вариациях ее параметров, вызванных изменением нагрузки, технологическим разбросом параметров и их старением, внешними воздействиями, погрешностями вычислений и погрешностью модели объекта.
Исследуем нашу систему на робастность. Для этого мы заменим числитель не некоторый коэффициент K, а второе слагаемое в знаменателе на A. Данные коэффициенты учитывают варьирование характеристик электродвигателя таких как индуктивность, момент инерции и т.д.
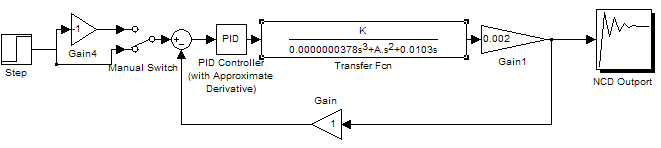
Рис. 20 Схема исследования системы на робастность.
Применяем NCD блок, в нем зададим максимальное коэффициентов +20% и минимальное -20% значения этих коэффициентов.
Рис. 21 Настройка NCD блока
Применив NCD блок мы получаем, значение коэффициентов PID-регулятора с учетом варьирования параметров системы: Kp= 65.28 Ki= 0.065 Kd= 1.96
Проверим данные коэффициенты, подставив их в систему с различными комбинациями коэффициентов K и A.
Рис. 22 Реакция системы на единичное ступенчатое воздействие при K=0.8 А=0.0002576
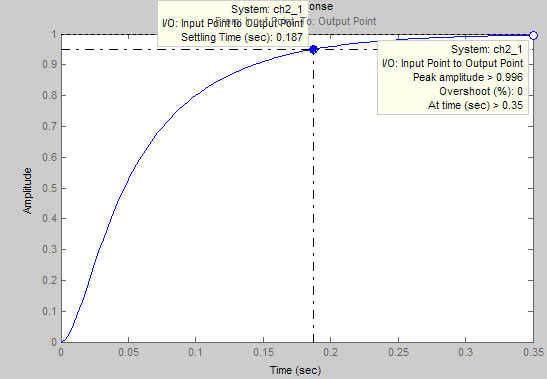
Рис. 23 Реакция системы на единичное ступенчатое воздействие при K=1.2 А=0.0002576
Рис. 24 Реакция системы на единичное ступенчатое воздействие при K=1.2 А=0.0003864
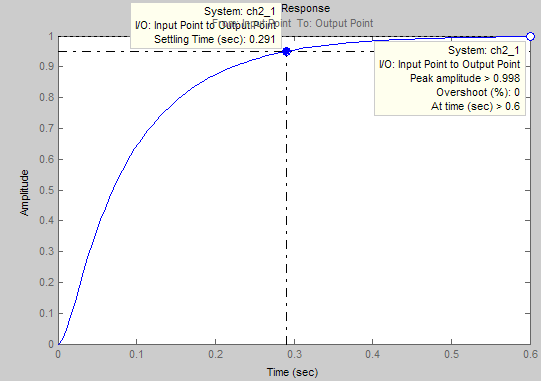
Рис. 25 Реакция системы на единичное ступенчатое воздействие при K=0.8 А=0.0003864
В результате мы видим что наша система во всех случаях не теряет устойчивость , не становится колебательной, но в 2-х увеличивается время переходного процесса, появилась ошибка, но в общем виды наших систем подходит по техническому заданию.