Министерство образования Республики Беларусь

Белорусский национальный технический университет

Кафедра «Стандартизация, метрология и информационные системы»

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

К курсовому проекту

по дисциплине

«Нормирование точности и технические измерения»

Исполнитель: __________ Райхлин М.Ю.

Студент 3 курса гр. 103510

Руководитель: __________ Боровец Г.В.

Минск 2013

Содержание

Содержание 3

2. Расчет калибров для контроля деталей гладких цилиндрических сопряжений 6

5. Расчет допусков и посадок шпоночного соединения 11

Задача №6 Расчет допусков и посадок резьбовых сопряжений 14

6.1. Расчет резьбовой посадки m48-7g/6h 14

Рассчитываем предельные размеры отверстия Ø240H8.

По ГОСТ 25346-89 определяем значения допуска IT8 = 72 мкм

Нижнее отклонение будет равно

EI = ES - IT8 = 72 - 72 =0 мкм.

Верхнее отклонение будет равно

ES = EI + IT8 = 72 мкм.

Предельные размеры вала:

D_max = D₀ + ES = 240,000 + 0,072 = 240,072 мм.

D_min = D₀ + EI = 240,000 + 0= 240,000 мм;

Рассчитываем предельные размеры вала Ø240m7.

По ГОСТ 25346-89 «Основные нормы взаимозаменяемости. Единая система допусков и посадок. Общие положения, ряды допусков и основных отклонений» определяем значения допуска IT7= 46 мкм и основного (верхнего) отклонения es =63 мкм.

Нижнее отклонение будет равно

ei = es- IT6 =63 – 46 = 17 мкм.

Предельные размеры отверстия:

d_max = d₀ + es = 240,000+0,063 = 240,063 мм;

d_min = d₀ + ei = 240,000 + 0,017= 240,017 мм.

Результаты расчётов оформим в виде таблицы.

Таблица 2

Размер	IT, мкм	ES (es), мкм	EI (ei), мкм	Dmin(dmin), мм	Dmax(dmax), мм
Ø240H8	72	+72	0	240,000	240,072
Ø240m7	46	+63	+17	240,017	240,063

Расчёт предельных размеров деталей сопряжения

D_ср = (D_max + D_min)/2 = (240,072 + 240,000)/2 = 240,036 мм;

d_ср = (d_max + d_min)/2 = (240,063 + 240,017)/2 = 240,040 мм;

S_max = D_max – d_min =240,072 – 240,017= 0,055 мм;

N_max = d_max – D_min = 240,017– 240,000= 0,063 мм;

Допуск посадки

T(S,N) = IT(D) + IT(d) = 0,072 + 0,046 = 0,118 мм.

Строим схему расположения полей допусков сопрягаемых деталей

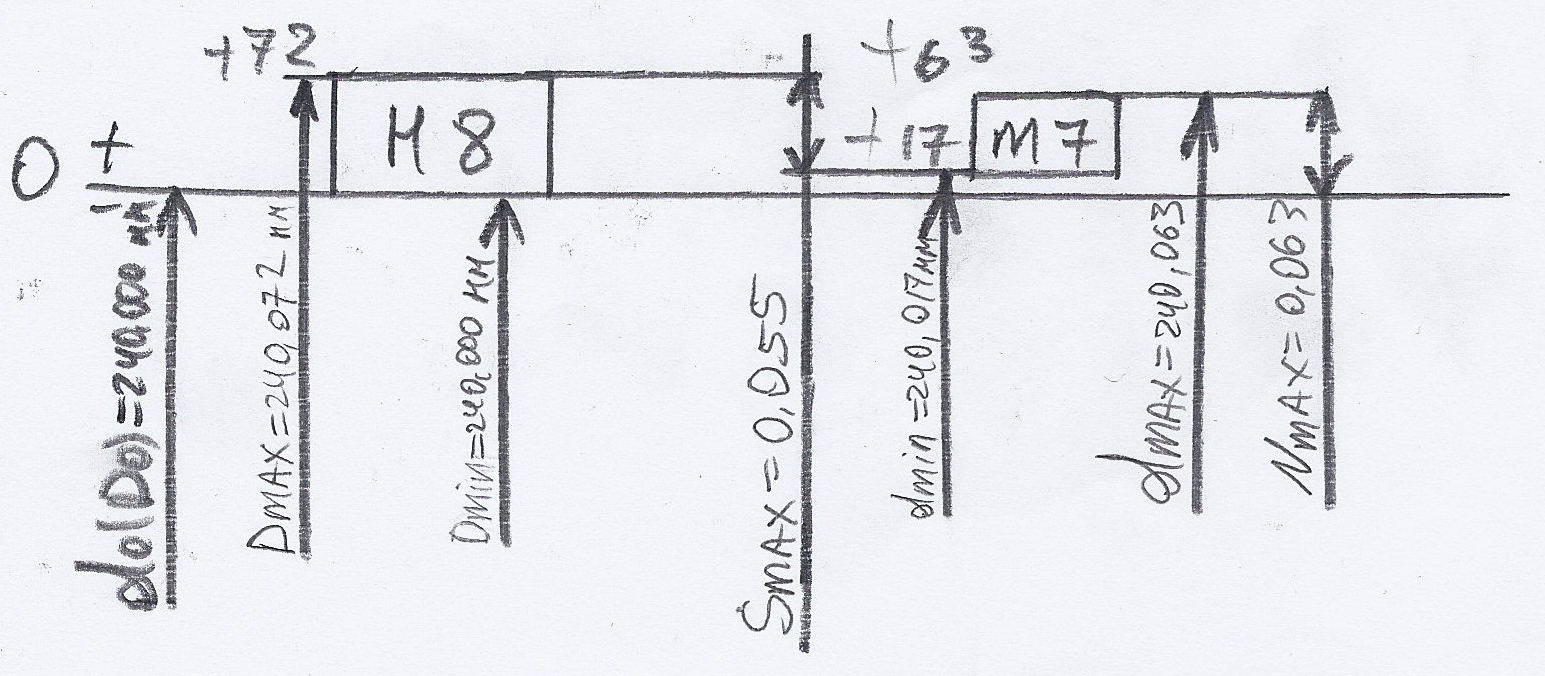
Рис.1.2.1. Схема расположения полей допусков сопрягаемых деталей

Принимаем нормальный закон распределения случайных размеров и рассчитываем предельные значения вероятных зазоров (натягов). В рассматриваемом сопряжении D_cp<d_cp, поэтому рассчитываем вличину математического ожидания зазоров:

M(S) = D_ср – d_ср =240,036 – 240,040 = -0,004 мм;

мкм

Рассчитаем предельные значения вероятных зазоров и натягов:

S_max.вер. = M(S) + 3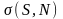 = -4+ 314,24 = 38,72мкм ≈0,038мм ;

S_min.вер. = M(S) – 3 = -4 – 314,24 = -46,72мкм ≈ -0,046мм ;

N_max.вер = 46,72 мкм = 0,046 мм.

При применении переходных посадок в спряжениях возможны зазоры или натяги. Поэтому рассчитываем вероятность их получения. Для определения площади заключенной между кривой Гаусса, осью ординат и осью абсцисс (на чертеже указанная площадь заштрихована) используем табулированные значения функции.

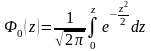, где .

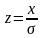В данном случае

х = M(S) =4 мм;

= 14,24 мкм.

Тогда

z = M(S) / =4/14,24 =0,28;

Ф(z=0,28) =0,1103= 11,03 %

Таким образом, вероятность получения зазоров в сопряжении Ø240H8/m7 составляет Р(S) = 50 % + 11,03 % = 61.03 %.

Определим вероятность получения натягов Р(N) =38,97 %.

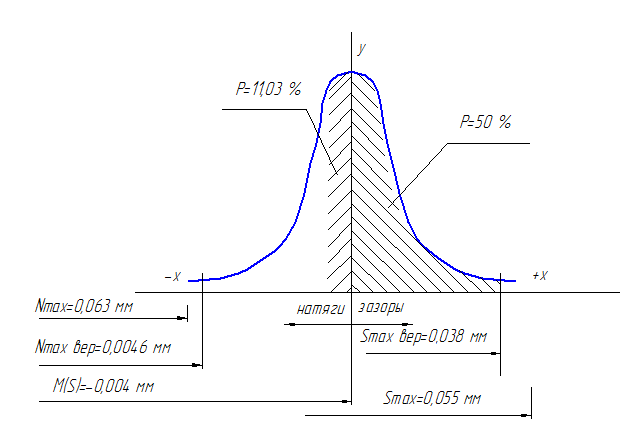
Рис.1.4. Распределение вероятных зазоров (натягов)