64.Теорема о производной определенного интеграла по переменному верхнему пределу

 Интеграл с переменным верхним пределом. Значение определённого интеграла не зависит от того, какой буквой обозначена переменная интегрирования:   (чтобы убедиться в этом, достаточно выписать интегральные суммы, они совпадают). В этом разделе переменную интегрирования будем обозначать буквой t, а буквой x обозначим верхний предел интегрирования. Будем считать, что верхний предел интеграла может меняться, т.е. что x - переменная, в результате интеграл будет функцией Ф(x) своего верхнего предела:  . Легко доказать, что если f(t) интегрируема, то Ф(x) непрерывна, но для нас важнее следующая фундаментальная теорема:  Теорема об интеграле с переменным верхним пределом. Если функция f(t) непрерывна в окрестности точки t = x, то в этой точке функция Ф(x) дифференцируема, и  .  Другими словами, производная определённого интеграла от непрерывной функции по верхнему пределу равна значению подынтегральной функции в этом пределе.  Док-во. Дадим верхнему пределу x приращение  . Тогда    , где c - точка, лежащая междуx и   ( существование такой точки утверждается теоремой о среднем; цифры над знаком равенства - номер применённого свойства определённого интеграла).  . Устремим  . При этом   (c- точка, расположенная между x и  ). Так как f(t) непрерывна в точке t = x, то . Следовательно, существует   , и  . Теорема доказана.

Отметим первое важное следствие этой теоремы. По существу, мы доказали, что любая непрерывная функция f(x) имеет первообразную, и эта первообразная определяется формулой  . Другим важным следствием этой теоремы является формула Ньютона-Лейбница, или основная формула интегрального исчисления.

65. Формула Ньютона — Лейбница

Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке.

Тогда

Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).

66.Свойства определенного интеграла.

Свойства определенного интеграла:

1)

2)

3)

4)

5)

Если функция интегрируема на [a; b], то она интегрируема на любом отрезке

Если f (x) – периодическая функция с периодом T, то для любого a

|f (x)| интегрируема на [a; b], причем

67.Теорема о среднем значении определенного интеграла на отрезке

Пусть функция f(x) непрерывна на [a, b], тогда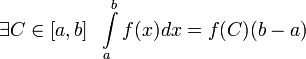 

Доказательство:

1. По свойству функции, непрерывной на отрезке,  , такие что  .

2. По свойству определенного интеграла  , следовательно  ,  . Обозначим дробь как m ^* .

3. Так как непрерывная функция принимает все свои промежуточные значения, а  , то  , такая что 

68. Геометрические приложения определенного интеграла.

Вычисление площадей плоских фигур

И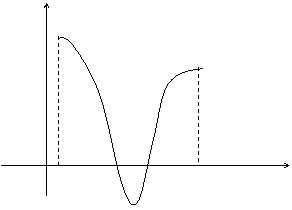 звестно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.

 Для нахождения суммарной площади используется формула: .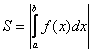

Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.

  Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x², x = 2  Искомая площадь может быть найдена по формуле:

(ед²)

П лощадь фигуры, ограниченной кривыми y=f₁(x) и y=f₂(x), [f₁(x)≤f₂(x)] и прямыми х=а и х=b, находится по формуле:

      Пример. Вычислить площадь фигуры, ограниченной заданными линиями y=–x², y=–x–2.      Решение.      Найдем абсциссы точек пересечения данных линий: x₁=–1,x₂=2.      Значит,                   =–3+1,5+4+2=4,5.

О бъем тела, полученного вращением криволинейной трапеции вокруг оси Ох; находится по формуле: 

Длина кривой, заданной уравнением y=f(x), a ≤x≤b,выражается следующим образом: