7 Виды математических систем
8 Отличия между нелинейными и линейными процессами
В отличие от линейной системы не обладает свойствами суперпозиции, частота выходного сигнала зависит от его амплитуды и др. Порядок установки линейных систем не влияет на результирующий сигнал. Любая сложная система будет линейна, если составлена из линейных систем и блоков суммирования. Перемножение сигнала на константу является линейной операцией, а перемножение двух сигналов — нелинейной.
9 Динамические системы
Динамическая система — математическая абстракция, предназначенная для описания и изучения систем, эволюция во времени которых однозначно определяется начальным состоянием. Динамическая система представляет собой математическую модель некоторого объекта, процесса или явления. Основное содержание теории динамических систем — это исследование кривых, определяемых дифференциальными уравнениями. Сюда входит разбиение фазового пространства на траектории и исследование предельного поведения этих траекторий: поиск и классификация положений равновесия, выделение притягивающих (аттракторы) и отталкивающих (репеллеры) множеств (многообразий). Важнейшие понятие теории динамических систем — это устойчивость (способность системы сколь угодно долго оставаться около положения равновесия или на заданном многообразии) и грубость (сохранение свойств при малых изменениях структуры динамической.
10 Моде́ль Ло́тки — Вольтерра́
Моде́ль
Ло́тки — Вольтерра́ — модель
межвидовой конкуренции, которые
предложили модельные уравнения независимо
друг от друга. Такие уравнения можно
использовать для моделирования систем
«хищник-жертва», «паразит-хозяин»,
конкуренции и других видов
взаимодействия между двумя видами В
математической форме предложенная
система имеет следующий вид:
где:
—
количество жертв
—
количество хищников
—
время
, 
, 
и 
—
коэффициенты, отражающие взаимодействия
между видами
11 Ряд Те́йлора
Ряд
Те́йлора — разложение функции в бесконечную
сумму степенных функций. Пусть
функция 
бесконечно
дифференцируема в некоторой окрестности точки 
.
Формальный ряд
называется
рядом Тейлора функции 
в
точке 
.
13. Графическое представление фазового портрета системы двух ДУ
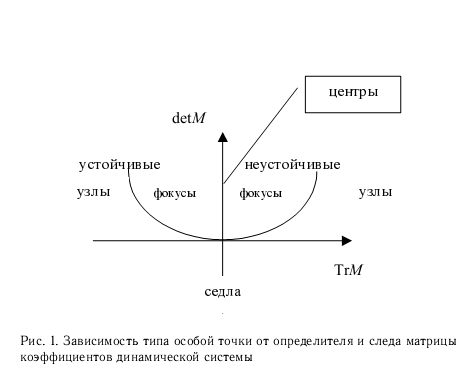
14. Структурная устойчивость и бифуркация
15. Классификация точек покоя. Устойчивый узел
16. Классификация точек покоя. Неустойчивый узел
17. Классификация точек покоя. Седло
18. Классификация точек покоя. Устойчивый фокус
19. Классификация точек покоя. Неустойчивый фокус
20.Классификация точек покоя. Центр
21.Классификация точек покоя.Предельный цикл.
В теории динамических систем и дифференциальных уравнений, предельным циклом векторного поля на плоскости или, более обобщённо, на каком-либо двумерном многообразии называется замкнутая (периодическая) траектория этого векторного поля, в окрестности которой нет других периодических траекторий. Эквивалентным является утверждение, что всякая достаточно близкая к предельному циклу траектория стремится к нему либо в прямом, либо в обратном времени.