23. Многомерное шкалирование. Теорема Янга-Хаусхолдера. Метрическое шкалирование в метрическом шкалировании укажем два метода: ординация Орлочи и метод главных проекций Торгерсона.

Ординация Орлочипредставляет собой сравнительно простой геометрический метод. По матрицеGвначале выбирают две наиболее различающиеся (удаленные) точки (i,j = 1,2,…,N).

Прямая, проходящая через эти две точки, принимается за первую ось. Обозначим ее A₁A₂(рис.15).

Рис.15. Ординация Орлочи

Проекции (координаты) остальных точек на первую ось, как видно из рис. 15, составят

.

Строится матрица расстояний по найденным координатам, которая сравнивается с матрицей различий. Если соответствие приемлемое, решение достигнуто; в противном случае необходимо искать вторую ось, проходящую через точку, наиболее удаленную от прямой .Очевидно, это точка, которая доставит максимум,j=3,4,…,N.

Координаты остальных точек – проекции на полученные оси – можно получить геометрическим построением либо аналитически. Однако повышение размерности приводит к сложностям получения оценок. К тому же решение оказывается излишне чувствительным к данным, поскольку оно определяется всего по нескольким точкам.

В методе главных проекций Торгерсона предполагается, что матрица G– матрица евклидовых расстояний между объектами, не содержащая ошибок. По матрицеGнеобходимо определить размерность пространства и проекции точек на его оси. Пусть– расстояния между точкамиi, j, k(рис.16).

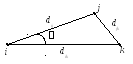
Рис. 16. Графическая иллюстрация скалярного произведения

Вычислим симметричную матрицу B_i размерностиN×N с элементамиb_jk , представляющими скалярное произведение векторов с началом в точкеiи концами в точкахj иk:.

Любая из N точек может быть взята в качествеi-й. Таким образом можно получитьN возможных матрицB_i. Согласно теореме Янга-Хаусхолдера:

1. Если какая-либо B_i (i=1,2,…,n) является положительно полуопределенной (ППО), то различия между объектами можно рассматривать как расстояния между точками в вещественном евклидовом пространстве.

2. Ранг любой ППО матрицы соответствует размерности rмножества точек. (Напомним, то ранг ППО матрицы равен числу положительных собственных значений.)

3. Любую ППО матрицу можно факторизовать в виде B_i=XX′. ЭлементыХесть проекции точек-объектов наr ортогональных осей вr-мерном вещественном пространстве с центром в точкеi.

Для того чтобы уменьшить влияние возможных ошибок, начало координат помещают в центр тяжести всех объектов. Тогда координаты искомых (центрированных) точек будут иметь вид:

.

Матрица скалярных произведений новых переменных должна факторизоваться в виде. Подставляя сюда выражение для центрированных переменных и выражая координаты через расстояния можно получить, что, где.

Легко видеть, что .

Матрицу называют матрицей сдвойным центрированием.Факторизация матрицыпроводится так же, как и в факторном анализе (см. п. 11.2).

В алгоритме Торгерсона предполагается, что матрица различий является и матрицей расстояний, т.е. G = D. Это требование можно ослабить, допуская, что матрица различий может быть преобразована в матрицу расстояний с помощью аддитивной константы, т.е.D = G + C,

где С– матрица, по главной диагонали которой стоят нули, а остальные элементы – одно и то же числос(аддитивная константа).

Эта константа должна быть такой, чтобы разместить объекты в вещественном пространстве возможно меньшей размерности. Так, для матрицы

аддитивная константа есть с=5.

Преобразованная матрица

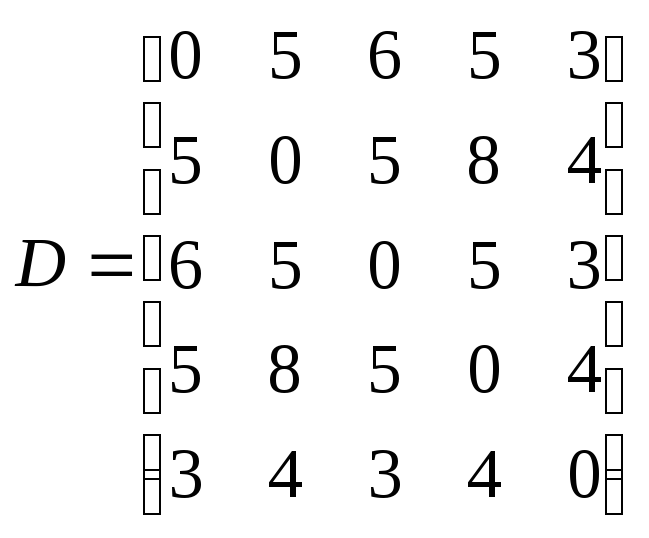
стала матрицей расстояний пяти точек на плоскости (рис.17).

Рис.17. Конфигурация точек для матрицы расстояний D

Отметим, что при с<5 разместить объекты в вещественном евклидовом пространстве невозможно (не выполняется правило треугольника), прис>5 размерность превышает 2.