Федеральное государственное общеобразовательное учреждение

высшего профессионального образования

Пермская государственная сельскохозяйственная академия

имени академика Д.Н.Прянишникова

Факультет землеустройства и кадастра

Кафедра земельного кадастра

КОНТРОЛЬНАЯ РАБОТА № 1

«Решение задач линейного программирования

симплексным методом»

Вариант № 57

Выполнил ст. гр. Гк-41б

А.В. Гердт____________

«____»_____________2012

Проверил преподаватель

Д.Э. Сетуридзе_______

«____»_____________2012

Пермь 2012

Содержание

1. Решение задачи линейного программирования графическим способом.

2. Решение задачи линейного программирования симплексным методом (с анализом последней симплексной таблицы и двойственных оценок).

3. Решение задачи линейного программирования симплексным методом с искусственным базисом.

4. Составление двойственной задачи.

1.Решение задачи линейного программирования графическим способом

Задачи линейного программирования решаются графическим способом если количество переменных меньше или равно 2.

Исходные данные.

Графическим методом найти max и min значение целевой функции:

Z = 6X₁ + 4Х₂

При ограничениях:

Х₁+4Х₂1000

0,05Х₁ + 0,03Х ₂≤400

Х₁≤300 Х₂≤600

Х₁0

Последовательность решения:

1. Для решения задается система координат.

2. Неравенства записываются в виде уравнений. Одна из переменных приравнивается к "0" и по решению уравнения находим значение второй переменной, затем вторая переменная приравнивается "0" и находится значение первой переменной. По двум точкам строится прямая и обозначается ОДЗ этой прямой.

1 уравнение: Х₁+4Х₂=1000

Х₁ = 0;Х₂ =2500

Х₂ = 0; Х₁ = 1000

2 уравнение: 0,05Х₁ + 0,03Х ₂ =400

Х₁ = 0;Х₂=13333,3

Х₂ = 0; Х₁ = 8000

3 уравнение: Х₁ = 300

4 уравнение: Х₂ = 600

Вывод: ОДЗ отсутствует, это означает, что нет пар переменных (Х) которые отвечали поставленным условиям, это случается когда условия противоречат друг другу. Система несовместима и не имеет общего решения.

2.Решение задачи линейного программирования симплексным

методом

Симплексный метод является универсальным методом, позволяющим находить оптимальное решение большого количества задач линейного программирования.

Такие задачи содержат много переменных и ограничений, ОДЗ этих задач представляет собой многогранник.

Для отыскания оптимального плана или вершины производится вычисления по определенному алгоритму.

Исходные данные.

Решить симплексным методом 3Х₁ - Х₂ + 5X₃ → max.

Х₁ + 2Х₂ +3Х₃≤ 100

2Х₁ + 8Х ₂ +5Х₃≤ 1200

2Х₁ - 3Х ₂ ≤ 10

Х₁ + Х₃≤ 20

Последовательность решения:

Симплексный метод является универсальным, он позволяет находить оптимальное решение большого количества любых задач линейного программирования.

На первой стадии приводят задачу к канонической форме:

Х₁ + 2Х₂ +3Х₃+ S₁= 100

2Х₁ + 8Х ₂ +5Х₃+ S₂= 1200

2Х₁ - 3Х ₂ + S₃=10

Х₁ + Х₃+ S₄ =20

Z = 3X₁ - X₂ + 5X₃ +0S₁+ 0S₂+ 0S₃+ 0S₄ → max

Далее находят количество небазисных переменных как разность количества переменных (n) и количества ограничений (m).

В данном случае, n=7 (Х₁; Х₂; Х₃; S1; S₂; S₃; S₄) и m=4. Следовательно, количество небазисных переменных равно трем.

Формальным признаком оптимальности плана является содержание индексной строки. Данная задача решается на определение максимума, поэтому план будет оптимальным, когда в индексной строке будут отсутствовать отрицательные коэффициенты.

В первую симплексную таблицу записываются числовые значения, взятые из ограничений и функции цели (таблица 1).

В индексной строке при условии максимума по абсолютной величине число (-) среди отрицательных коэффициентов. Этот коэффициент означает главный столбец – k.

Далее определяют, какую базисную переменную необходимо вывести из плана. Это определяют через симплексное отношение, то есть через отношение свободных членов базиса на соответствующие коэффициенты главного столбца .

Выбирается наименьшее положительное неравное нулю симплексное отношение. Эта строка является главной.

Затем определяют главный элемент (а_kl) на пересечении главного столбца с главной строкой.

Вторая симплексная таблица заполняется следующим образом:

1. Заполняются коэффициенты главной строки как отношение старых элементов к главному элементу:

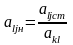
2. Заполняются коэффициенты по старому главному столбцу. Применяется процедура на основе системы Гаусса, где все элементы принимаются за нуль.

3. Все прочие элементы заполняются по правилу прямоугольника – берем главный элемент и бывшее значение и через эти две строим прямоугольник. От старого значения отнимаем дробь, где в знаменателе показатель главного элемента, а в числителе произведение не задействованных элементов противоположных углов прямоугольника.

Таблица 1 - Первая симплексная таблица

Оценка базисной переменной	Базисная переменная	Базис (план)	Основные переменные				Дополнительные переменные						Симплексное отношение
			Х1	Х2	Х3	S1		S2		S3	S4
0	S1	100	1	2	3	1		0		0	0	33,3
0	S2	1200	2	8	5	0		1		0	0	240
0	S3	10	2	3	0	0		0		1	0	0
0	S4	20	1	0	111 1	0		0		0	1	20
Индексная строка		0	-3	1	-5	0		0	0		0

Таблица 2 - Вторая симплексная таблица

Оценка базисной переменной	Базисная переменная	Базис (план)	Основные переменные				Дополнительные переменные
			Х1	Х2	Х3	S1		S2	S3	S4
0	S1	40	-2	2	0	1		0	0	0
0	S2	1100	-3	8	0	0		1	0	0
0	S3	10	2	3	0	0		0	1	0
5	X3	20	1	0	1 1	0		0	0	1
Индексная строка		100	2	1	0	0		0	0	0

Ответ: Х₁=0; Х₂=0; Х₃=20; S₁=40; S₂=1100; S₃=10; S₄=0.

Проверка: 1) 0+2*0+3*20+40=100

100=100

2) 2*0+8*0+5*20+1100=1200

1200=1200

3) 2*0 – 3*0+10=10

10=10

4) 0+20+0=20

20=20

5) Z =3*0 – 0 +5*20 =100