12. Метод поиска в глубину с возвращением. Привести пример применения.

Данный метод обеспечивает получение всех вариантов решений, но приводит к другому порядку получения этих решений, нежели при поиске в ширину.

М ножество М в этом случае на первом шаге разбивается на множества и (дополнение), М₁ разбивается на и и т.д. до тех пор, пока по данной ветви не будет получено подмножество, содержащее только один вариант. Далее выполняется возвращение к ближайшему подмножеству, содержащему более одного варианта, и процедура применяется к этому подмножеству. Данный процесс продолжается до тех пор, пока не будут получены все подмножества вариантов.

Пример метода поиска в глубину:

Исходный граф:

Процесс поиска (номерами указан порядок рассмотрения вершин.)

13. Метод поиска в ширину. Привести пример применения.

Рассмотрим следующий граф:

Р ассмотрим задачу поиска всех маршрутов, т.е. простых цепей выбранного графа, соединяющих вершину с .

Выберем принцип формирования маршрута – последовательное включение в простую цепь ребер в порядке возрастания их номеров.

Принцип разбиения в данном случае вытекает из принципа формирования маршрута.

Порядок разбиения подмножеств решений будем осуществлять в соответствии со стратегией декомпозиции ‘в ширину’: переход с одного уровня дерева декомпозиции к другому будем осуществлять только после включения в строящиеся цепи текущего ребра. Результат такого поиска показан ниже:

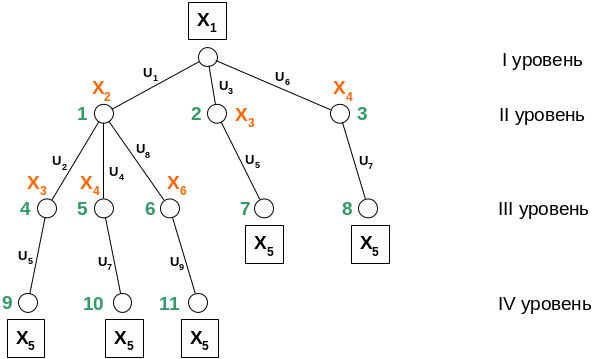
Данный метод осуществляет полный перебор и гарантирует нахождение точного решения.

14. Идея метода ветвей и границ. Основные способы отсечения ветвей.

Регулярный, но достаточно сложный метод решения комбинаторно-оптимизационных задач. Решение ищется посредством направленного перебора вариантов.

Сокращение количества просмотренных вариантов достигается как за счет организации ветвления, так и за счет отсечения подмножества вариантов, не содержащих оптимального решения.

Ветвление может осуществляться, как по методу в ширину, так и по методу в глубину с возвращением.

Реализация метода: принцип разбиения вариантов на подм-ва и вычисление условий отсечения существенно зависят от вида задачи, т.е. св-в исследуемого графа. Степень сокращения перебора зависит от кач-ва оценочной функции, стратегии декомпозиции и исходных данных, учитываемых характеристик объекта. # соотношение весов ребер.

В худшем случае метод может вылиться в полный перебор. Организация ветвления заключается в выборе в соответствии с оценочной функцией очередной вершины, подм-во вариантов которой будет декомпозировано на след. шаге и отсечения тех вершин, подм-во вариантов которых не содержат оптимального.

Способы отсечения ветвей:

• Сравнение оценки(т.е. верхней или нижней границы со значением целевой функции некоторого уже найденного решения). Опорное решение может быть получено заранее приближенным алгоритмом, либо найдено в ходе решения задачи методом ветвей и границ(на предыдущих шагах).

• По результатам сравнения 2-х оценок. Такое отсечение выполняется, если в задаче на min целевой ф-ции для мн-ва вариантов можно найти оценку сверху и снизу. Если для некоторого подм-ва вариантов: Mi Fн(Mi), Fв(Mi) а для подмножества M_j - F_н(M_j) и F_в(M_j), и Fн(Mj)>= Fв(Mi), то очевидно, что ветвление в вершине соответствующей подм-ву Mj надо прекращать

• Если по каким-либо др. оценкам известно, что данное подм-во не содержит оптимального решения или прекращение ветвления в особых вершинах (алгоритм Дейкстера).

Особенности метода ветвей и границ.

• Чем точнее получена оценка перспективности, т.е. чем ближе ее значение к целевой функции для оптимального варианта, тем < кол-во вершин дерева решений будет исследовано. То же самое относительно дерева опорного решения.

• Чем > будут отличаться значения оценочных ф-ций для текущих вершин дерева решений, тем < количество вариантов будет рассмотрено.

• Если сущ. несколько принципов разбиения мн-ва решений, необходимо выбирать тот, при котором оценки наиболее точны.

Основные способы ветвления при реализации метода ветвей и границ

1. Разбиение множества вариантов на подмножества по методу в ширину и выбор вершины по min(max) оценочной функции.

   1. Получают все вершины – потомки вершины нулевого уровня (либо часть этих вершин при модификациях метода).

   2. Далее на любом уровне выполняется декомпозиция очередного выбранного множества вершин.

   3. Если возможно, выполняется отсечение ветвей. В ходе построения дерева декомпозиции отсекающая оценка может уточняться.

2. Разбиение множества вариантов по методу поиска в глубину с возвращением с заранее заданным порядком ветвей.

   1. Строится полностью одна ветвь. Получаем опорное решение, значение целевой функции для которого может служить отсекающей оценкой.

   2. Далее ветвление выполняется последовательно в заданном направлении, начиная с вершины, предшествующей конечной.

   3. При этом любая ветвь достраивается до конца, если нет отсечения.

3. Комбинация декомпозиции в глубину и в ширину

   1. Строится одна ветвь по методу в глубину.

   2. Далее декомпозиция выполняется по методу в ширину с выбором очередной вершины по min или max оценочной ф-ции и использовании опорного решения.

Эффективность того или иного способа ветвления, т.е. степень сокращения перебора зависит от вида задачи и конкретных хар-к графа. От способа ветвления зависит степень сокращения перебора, но дать общих рекомендаций по выбору способа невозможно.

Оптимальное решение задачи будет найдено, если значение целевой функции для некоторой конечной вершины есть min среди всех конечных и меньше значения нижней границы для всех оставшихся «висячих» вершин.