Некоторые особенности оценочных функций

1. Оценочная функция может быть определена на любом подмножестве вариантов, либо только на некотором варианте. Во втором случае используемый принцип разбиения должен обеспечить получение только таких вариантов, на которых оценочная функция определена. Если генерация только таких вариантов не обеспечивает или затрудняет получение оптимального решения, то следует вернуться к анализу и конструированию другой оценочной функции. В частном случае оценочная ф-ция может совпадать по виду с целевой, однако это совпадение не обязательно. Значение оценочной ф-ции для конечной вершины дерева решений должно быть равно значению целевой ф-ции для соответствующего варианта. Следовательно, нижняя граница должна быть неубывающей ф-цией, а верхняя невозрастающей. Отсюда следует, что вид дерева решений зависит от оценочной функции.

2. Вид оценочной функции – это степень достоверности, с которой мы можем судить о наличии или отсутствии в подмножестве оптимального варианта, порождающего различные методы поиска по дереву решений. При полной достоверности того, что подмножество не содержит оптимального решения, данное подмножество следует исключить из процессов дальнейшего разбиения. Говорят, что отсекают ветви и вершины, следующие за вершинами, сопоставленными этому подмножеству. В противном случае оценка может быть использована для обоснования очередности разбиения подмножеств, т.е. выбора на каждом шаге процесса декомпозиции очередной, более перспективной, вершины дерева решений. На основании сказанного будем различать отсекающую оценку и оценку перспективности.

Вид оценочной функции, ее возможности определяются в значительной степени спецификой задачи, т.е вида и свойств графов являющихся моделями объекта и результата проектирования.

В качестве отсекающей оценки в ряде случаев может выступать текущее значение целевой функции, либо какая-то мера компонента графа.

Как правило, отсекающей оценкой является некоторый вариант решения данной задачи. Этот вариант называется опорным решением. Желательно получить его за минимально возможное время. Значение целевой функции для этого варианта и является отсекающей оценкой.

Действительно, если в задаче на поиск мин. значения целевой ф-ции нижняя граница для некоторого подмножества превышает значение целевой ф-ции решения для опорного решения, то данное подмножество не содержит оптимального решения.

11. Метод поиска в глубину. Пример точного алгоритма, основанного на этом методе.

Данный метод является вырожденным случаем разбиения пространства решений. Он заключается в том, что на каждом уровне дерева решений в соответствии с некоторой оценкой, определяемой спецификой задачи, выбирается одно подмножество, не формируя (отсекая) остальные, до тех пор, пока не получим решение. Таким образом, здесь формируется только одна ветвь дерева решений. Алгоритмы, основанные на этом методе, должны быть весьма эффективными в смысле затрат времени и памяти ЭВМ. Если оценка является отсекающей, т.е. с вероятностью равной единице, позволяет судить о том, что оптимальный вариант находится в данном подмножестве, получаем точное решение. В противном случае гарантируется лишь приближенное.

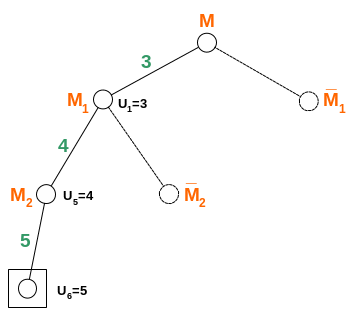
Примером точного алгоритма, основанного на этом методе, является алгоритм Прима.

Алгоритм Прима.

А лгоритм предназначен для построения минимального остовного дерева графа G.

Шаги:

1. Рассчитываются длины всех ребер графа, являющегося моделью исходного описания объекта.

2. Ребра ранжируются в порядке возрастания длины.

3. Из ребер, инцидентных вершинам построенного фрагмента дерева, выбирается ребро, имеющее минимальную длину и не образующего цикла с ребрами, уже включенными в дерево. На первом шаге выбирается ребро минимальной длины. Процесс заканчивается, когда все вершины соединены ребрами.

Общий вид работы алгоритма показан на рисунке слева. На нем использованы следующие условные обозначения:

-множество вариантов, содержащих ребро .

- множество вариантов, НЕ содержащих ребро .

И так далее.