5. Выбор аппарата формализации задач структурного синтеза. Разработка моделей объекта и результата проектирования, доказательство их адекватности (приведите пример перехода от объекта к модели).

Выбор аппарата формализации

Для задач структурного синтеза широко используется аппарат теории графов. В общем случае в качестве математической модели проектирования, то есть множество допустимых решений, надо использовать такую абстракцию, которая позволила бы точно и с требуемой точностью полноты отобразить компоненты объекта проектирования, отношения между ними, характеристики и свойства. Необходимо, чтобы существовал соответствующий аппарат, позволяющий выполнять преобразование модели первичного описания объекта, в модель результата.

Дополнительное требование является желательность наглядного представления модели.

В настоящее время аппарат теории графов достаточно развит: определены способы представления графов, операции над графами и способы их реализации над соответствующими представлениями графов. Сформулированы ряд теорем, лемм и методов решений широкого круга задач.

Разработка математической модели объекта и результата проектирования

Н

y2 (x4)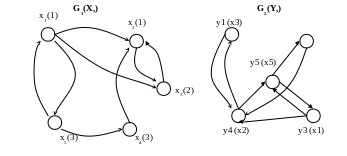

ередко математические модели объекта и результаты проектирования совпадают по виду

x1	x2	x3	x4	x5
y3	y4	y1	y2	y Два графа называют изоморфными, если один получается из другого путем переиндикации 5

Для получения математической модели результата или объекта проектирования необходимо:

• определить каким компонентам объекта необходимо поставить в соответствие элементы графа

• сформулировать правила сопоставления элементов (вид соответствий)

• определить соответствие между отношениями компонент-объекта и отношениями элементов графа таким образом, чтобы были правильно отображены свойства отношения объекта, отобразив в модели характеристики его компонентов

• отобразить в модели объекта характеристики его компонент

(вершины графа)

(ребер графа)

отношение

инцидентности:

Отношение

принадлежности

Отношение связности

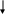
отношение смежности:

,

Таким образом моделью цепи будет неориентированный граф. Поскольку цепь не должна быть замкнутой, следовательно этот граф особого вида: дерево

Ребра этого дерева должны соединять все вершины => оставное дерево => моделью варианта цепи или результата проектирования является основное дерево. Так как существует понятие – взвешенный граф, модель позволяет отобразить характеристики компонентов в виде весов соответствующих элементов модели.

множество длин отрезков проводников: , где M – метрика

В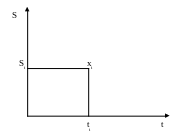 еса представляют собой пару координаты, соответствующего вывода и допустимое количествово проводников

Так как на n вершинах можно построить разных остовных деревьев, то все варианты модели структуры всей цепи будет граф, который будет состоять из t компонентов связности. таких, что

-- множество допустимых решений.

Модель проектирования для данной задачи является полный неориентированный граф , построенный на фиксированных вершинах, с взвешенными ребрами, для которого справедливо выражение:

теперь отражены все необходимые и достаточные для решения задачи компоненты объекта проектирования, их свойства, характеристики и отношения между ними, => обеспечена адекватность модели объекту.