28. Методика оценки вычислительной сложности алгоритма. Рассмотрите пример.

Пусть А – алгоритм решения некоторого класса задач, а n – размерность входа задач данного класса. Тогда вычислительная сложность – это f_A(n), отображающая размерность задачи в «математическое» время ее решения. Т.е. дающее оценку количества некоторых операций, необходимых для решения данным алгоритмом любой задачи данного класса функцией от размеров входа. Эта ф-ция является критерием качества алгоритма с т.з. временных затрат: эффективными являются полиномиальные алгоритмы, т.е. такие, у которых f_A(n) растет не быстрее, чем полином от n. Алгоритмы, имеющие экспоненциальную вычислительную сложность (2ⁿ, n! и т.п.), пригодны для решения задач ограниченной размерности.

Т.к. вычислительная сложность может быть представлена функциональной зависимостью числа операций, выполняемых алгоритмом, от парамтеров, характеризующих размерность задачи или объекта преобразований, либо оценкой вида О(n^к) или О(рⁿ), где к=1,2,.. n; р=2,3,… n. Оценку вычислительной сложности вида О(n^к) или О(рⁿ) можно получить, зная размерность задачи, по содержательному описанию алгоритма. При выполнении анализа необходимо учитывать, что: О(n)+О(n)=О(n), О(n)*О(n)= О(n²), О(n)+О(n²)=О(n²).

Задача называется n(p)-полной, если существует алгоритм, обеспечивающий ее решение за полиномиальное время.

Вычислительная сложность, так же как и погрешность, может иметь оценку в лучшем и в худшем. Оценка в худшем (сверху) получается в том случае, если входные данные являются худшими из возможных. Например, для задачи на графах, предположение, что граф – полный.

Улучшение верхней границы означает нахождение алгоритма с лучшей характеристикой в худшем. Как правило, это обеспечивает использование другого метода или других операций преобразования графа, либо специфических приемов снижения вычислительной сложности, направленных на оптимизацию алгоритма.

Однако ориентация на худший случай нередко приводит к пессимистическим оценкам, которые могут привести к неправильному выбору используемого алгоритма. Например, метод ветвей и границ в пределе, имеет экспоненциальную сложность, однако, в то же время, на многих задачах и наборах входных данных зависимость времени решения задачи этим методом от размера входных данных полиномиальна.

Более реалистичной является оценка в среднем. Для задач на графы такая оценка появляется при предположении, что граф – однородный с некоторой средней степенью вершин.

Асимптотическая оценка вычислительной сложности алгоритма

Точность функциональной оценки вычислительной сложности зависит от степени глубины проработки алгоритма и его анализа. На ранних этапах разработки алгоритма степень его детализации ограничена, а на завершающих этапах увеличивается трудоемкость анализа. Для использования вычислительной сложности в кач-ве глобального св-ва алгоритма широко используется асимптотическая оценка. Она задает «порядок». Основанием для использования таких оценок является тот факт, что многие практические задачи имеют большую размерность.

Используются асимптотические оценки двух видов: O(n) и o(n).

Функцию f(n) определяется как O((n)), и говорят, что она порядка (n) если

Порядок f(n) обозначают как f(n)= O((n))

Функция f(n) имеет порядок o((n)), если

Например, если f(n)=5n³-3n²+2n+6, то f(n)=О(n³), так как

И f(n)=о(n^3,1), так как

Рассмотрим пример оценки вычислительной сложности алгоритмической модели процесса свободной декомпозиции схемы соединения элементов ЭВМ по методу неуравновешенной двоичной свертки.

Моделью схемы является гиперграф H(X,U), в котором множествам элементов Э и цепей С схемы поставлены во взаимно-однозначные соответствия мн-ва вершин Х и ребер U. Гиперграф задан мн-вами вершин Х={xi / i=1}, ребер U={uj / j=1,m} и многозначными отображениями Х в U – ГХ ={Гxi / i=1,n} и U в Х – ГU = {Гuj / j=1,m}. Идея свободной декомпозиции схемы соединения элементов заключается в следующем: начиная с первого уровня (количество элементов, подлежащих объединению равно n), определяем показатели связности всех пар вершин графа.

, где Ui= Гxi, Uj= Гxj.

Далее процесс повторяется до тех пор, пока не останутся две последние вершины.

Получим оценку в худшем. Для этого предположим, что каждая вершина связана с каждой, а - максимальное количество выводов элементов схемы. Доминирующая операция при оценке вычислительной сложности – операция сравнения. Подсчет показателя связности вершин требует операций сравнения элементов мн-в Ui и Uj. Так как каждая вершина связана с каждой, то на некотором шаге t количество таких показателей будет равно

Алгоритмическая модель процесса свободной декомпозиции без учета операций корректировки гиперграфа имеет следующий вид ( выполняются пп. 1-3):

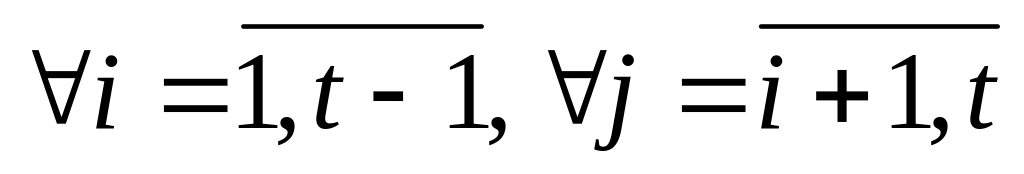1. : подсчитываем , где ,

2. Находим 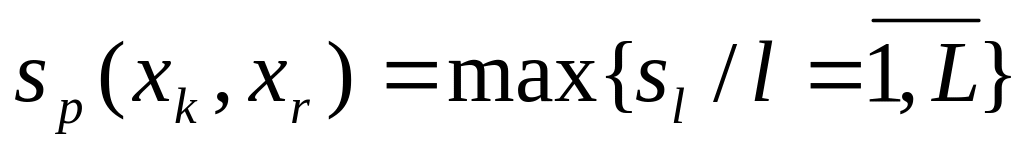, такой что

3. Объединяем в одну вершины х_к и х_r

Количество операций сравнения, необходимых для выполнения п.1. равно . Выбор пары вершин с максимальным показателем связности в п.2. потребует сравнений. Суммируя по получим:

В итоге