25. Детальная проработка алгоритма. Способы снижения вычислительной сложности алгоритмов. (Проиллюстрировать примерами).

Прежде чем приступить к детальной проработке алгоритма надо составить четкое представление о степени детализации и формализации его описания.

Назначение детального описания алгоритма – служить основной информацией для написания программы.

В том случае, если писать программу будет не разработчик алгоритма, нужна такая степень формализации и детализации, которая учитывала бы знание программистом соответствующего математического аппарата и не требовала от него восстановления опущенных разработчиком операций, как несущественных.

Для облегчения понимания описания формального описания алгоритма на языке теории графов, теории множеств, теории математической логики, целесообразно давать содержательные комментарии.

Форма записи операций над графами должна быть в максимально возможной степени приближена к конструкциям (операторам) выбранного языка программирования, а сам алгоритм должен строиться с учетом принципов системного программирования.

Степень детализации алгоритма может считаться приемлемой, если в любой конструкции алгоритма однозначно и полностью определено, над какими данными, какие операции и при каких условиях должны быть выполнены.

СПОСОБЫ СНИЖЕНИЯ ВЫЧИСЛИТЕЛЬНОЙ СЛОЖНОСТИ АЛГОРИТМОВ. (ПРОИЛЛЮСТРИРОВАТЬ ПРИМЕРАМИ).

На вычислительную сложность алгоритма влияют:

1. способ представления графа

2. структуры данных

3. способы вычисления анализируемых показателей и определение состава подмножеств, определяющих альтернативные решения

4. способы представления множеств и их свойств

Основные способы снижения вычислительной сложности циклических участков алгоритма:

1. использовать рекуррентных процедур для определенного состава таких множеств некоторых объектов (вершин или ребер графа, порождающих альтернативные варианты решения), которые в результате некоторых действий меняются лишь частично

2. применение рекуррентных формул или процедур для определения новых значений критериев или оценочных функций

Оценки количества ребер между двумя кусками гиперграфа схемы в процессе его последовательного разрезания:

Гиперграф - - множество вершин гиперграфа, смежных вершине . .

Аналогично если есть .

- среднее количество ребер инцидентных вершине.

- среднее количество вершин (элементов), содержащихся в ребре (цепи). На шаге i=n/2 гиперграф разрезан на куски Ø,

и получена . Надо определить на i-ом шаге , на котором в множество будет включена вершина

• - количество ребер, соединяющие хотя бы по одной вершине из и :

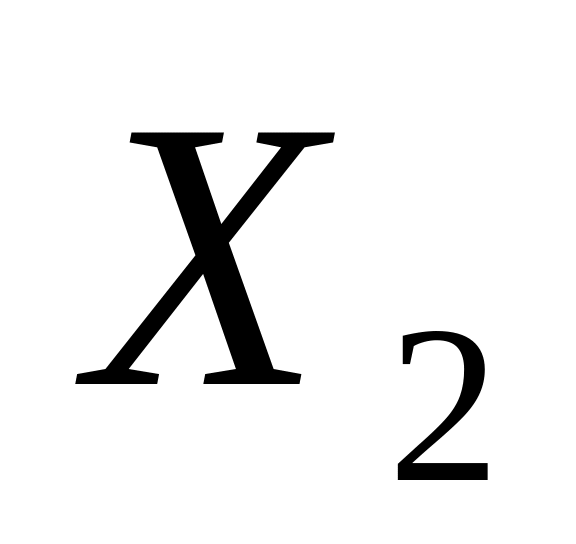потребует операций сравнения ребер, принадлежащих Для тоже самое суммарное количество операций сравнения для равно .

- среднее количество ребер в .

требует операций сравнения ребер этих подмножеств вычислительная сложность :

• количество ребер, находящихся в разрезе после выполнения i–первого шага, на

i-ом шаге может измениться только за счет изменения состояний относительно разреза ребер, инцидентных вершине , включаемой в на этом шаге останутся в разрезе ребра, содержащие хотя бы по одной вершине и или уйдут из разреза ребра, которые не содержат вершин или появятся в разрезе ребра, которые не содержат

- количество ребер, инцидентных вершине и появляющихся в разрезе и уходящих из него при включении вершины в . и ,

Условие появления:

Условие выхода:

Для проверки этих условий надо операций сравнения. Условия повторяются для всех , т.е. раз вычислительная сложность :

3. не повторять расчет значений некоторых оценок для тех вариантов возможных решений, для которых они после некоторых преобразований не меняются

Пример:

4. заранее выявлять и исключать из множества возможных вариантов решения, не удовлетворяющие заданным критериям

Пример:

В процессе декомпозиции схемы по методу двоичной свертки вначале определяем показатели связности всех пар вершин, имеющие общие ребра:

подсчитываем где - этим учитывается ограничение на показатель связности S>0 для всех вершин, не анализируя, связаны они или нет. При детальной проработке алгоритма надо оценить вычислительную сложность выполнения этой операции с предварительным анализом связности элементов схемы и без него и для ожидаемых значений характеристик схемы выбрать более эффективный вариант. Для полного графа или «близкого» к нему (ρ – не существенно меньше n-1), предварительный анализ связности элементов схемы приведет к увеличению вычислительной сложности, если же ρ<<n,m, можно ожидать, что предварительный анализ связности может снизить вычислительную сложность.

5. использовать дополнительные массивы, вектора (например, характеристические), позволяющие снизить вычислительную сложность реализации операции таких как ,например, , либо операций определяющих другие свойства элементов множеств, например, элементов алгоритма Краскала

6. использовать структуры данных, в том числе и комбинированные, которые обеспечивают снижение вычислительной сложности многократно повторяющихся операций