24. Определение операций преобразования исходного графа в граф результата. Выбор способа представления графов и его реализация в памяти эвм.

Операции преобразования исходного графа в граф результата необходимы для реализации метода решения задачи в виде алгоритма, для выбора способа представления графа и структур данных. Выбор операций должен быть направлен на обеспечение высокой эффективности алгоритма, низкой емкостной и вычислительной сложности и высокой точности результатов. Совокупность этих операций определяется по результатам анализа математической постановки задачи. Из нее нам известны:

1. граф, являющийся моделью математического описания объекта, его характеристики и свойства

2. вид, характеристики и свойства графа результата

3. целевая функция и ограничения задачи, зависящие от управляющих параметров, т.е. характеристик графа результата

Анализируя эту информацию и зная элементарные теоретико-множественные и алгебраические операции над графами, мы можем определить возможность операций преобразования исходного графа в граф результата.

Основные элементарные операции преобразования:

1. удаление

2. добавление

3. разбиение

4. стягивание или свертка

5. установление соответствия и раскраски вершин или ребер

Пример:

Дано – полный граф со взвешенными ребрами .

Найти – остовное дерево минимального веса, т.е. сделать преобразования:

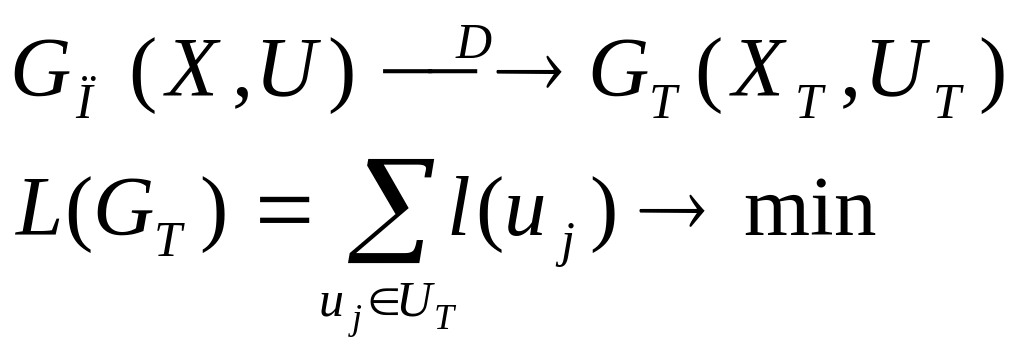
Ограничение - и - связанный граф:

Решение – т.к. , то - это суграф. Т.о. суграф получается путем удаления из графа части ребер. Значит для построения надо из удалить часть ребер. Т.к. нам нужно получить минимального веса предполагаем, что удалять надо последовательно ребра максимального веса. Примем без доказательства, что удаляя ребра максимальной длины, получим точное решение. Количество таких операций: k=m–n+1. При любом удалении ребра надо определить остается ли граф связным. Но точный алгоритм Прима и Краскала используют другую операцию – добавление ребер минимального веса. Выполним сравнительную оценку алгоритма, использующего операцию удаления, и алгоритм Краскала.

Алгоритм Краскала – ребра упорядочиваются по увелечению длины, т.е. начальное значение Ø) имеется компонент связности, далее из множества упорядоченных ребер выбираются те, которые имеют меньший вес и не образуют частных циклов. Количество операций добавления ребер равно k=n-1. При включении нового ребра надо проверять не образовался ли новый цикл.

	Алгоритм удаления ребер максимальной длины	Алгоритм Краскала
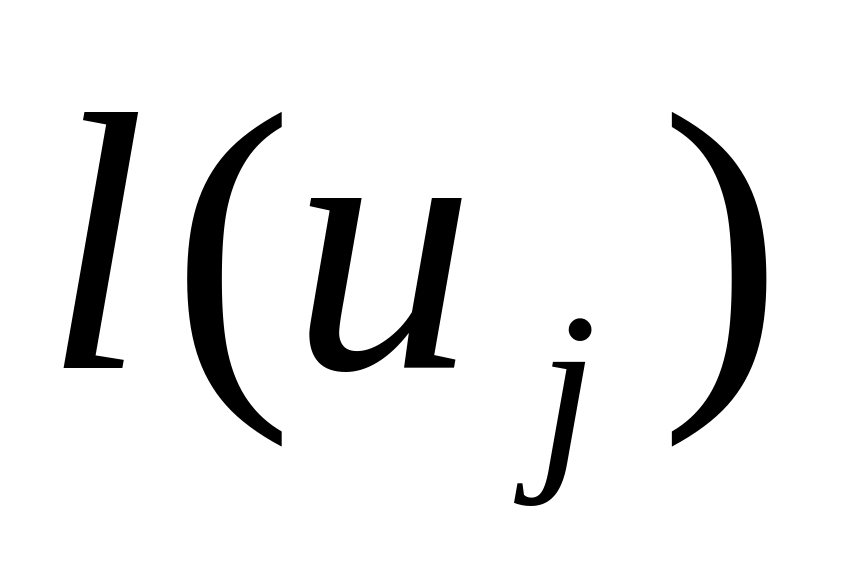
1) Предварительное упорядочивание	По убыванию	По возрастанию
2) Количество операций	m-n+1	n-1
3) Проверяемые свойства (характеристика)

Из 1) и 2) можно сделать вывод

Пр(х)	1	2	3	4	5	6
1 шаг	1	2	3	4	4	6

Из 1), 2) и 3)

Любая вершина – один компонент связности. 4,4 – а можно было написать 0,0 – безразлично.

Проверка реализуется проверкой принадлежат ли вершины ребра разным компонентам связности. Вычислительная сложность О(1).

ВЫБОР СПОСОБА ПРЕДСТАВЛЕНИЯ ГРАФОВ И ЕГО РЕАЛИЗАЦИЯ В ПАМЯТИ ЭВМ.

Способы представления графов:

1. неориентированный граф

2. гиперграф

Базовые структуры для хранения массивов данных:

1. вектор

2. матрица

3. линейный односвязный список

Основные варианты реализации графов в памяти:

1. матрица смежности и инцидентности

2. массив статических векторов

3. массив статических векторов с указателями начала каждого вектора

4. вектора с граничными условиями

5. массив динамических векторов

6. массив списков

7. список векторов

8. список списков

9. массив n-связных списков

10. список n-связных списков

Основное положение – от способа представления графа и его реализации в ЭВМ в значительной степени зависит его вычислительная и емкостная сложность алгоритма. В общем случае обработка данных включает в себя операции их преобразования в целях получения графа результата и их коррекцию. Выбор способа представления графа определяет операции его преобразования.

Возможные способы представления гиперграфа :

1) 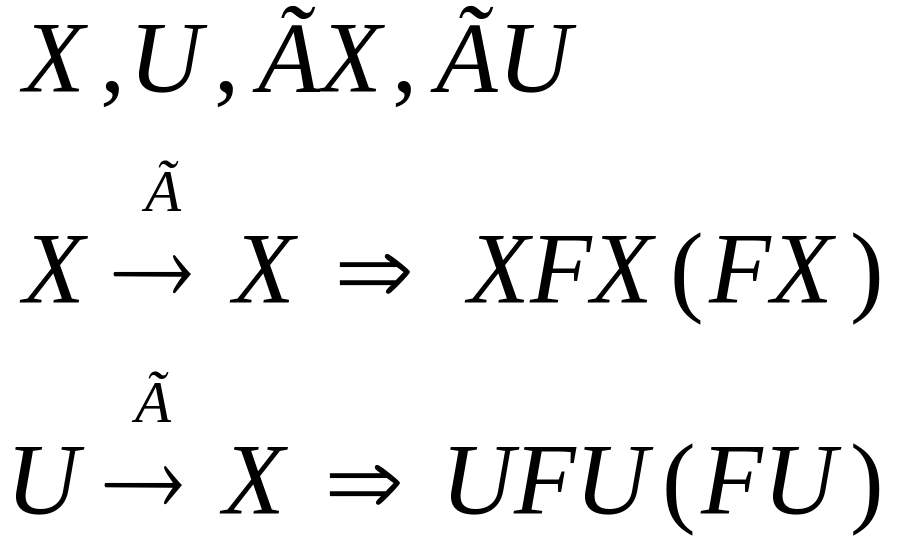2) 3) 4) 5)

Определяем множество элементов, соединенных цепью :

,

К- количество операций. Для все аналогично.

При разработке алгоритма решения задачи мы исходим из того, что коррекция данных уже выполнена (ошибки исправлены). Но эта посылка не означает, что в ходе работы алгоритма не может возникнуть необходимость в выполнении операций удаления, добавления вершин или ребер исходного графа или промежуточного результата решения задачи. Это зависит от существа задания и метода решения, т.е. от операции выполняемой над графом.

Для ряда заданий эта коррекция может выполняться после применения алгоритма (например, последовательный алгоритм разбивания гиперграфа). В других алгоритмах, например, реализующих метод свертки, операции коррекции надо выполнять на любом шаге алгоритма.

Например, в алгоритме свободной декомпозиции схемы по методу неуравновешенной двоичной свертки после факторизации вершин надо выполнить коррекцию аналитического представления гиперграфа:

1. Из Х удалить и добавить

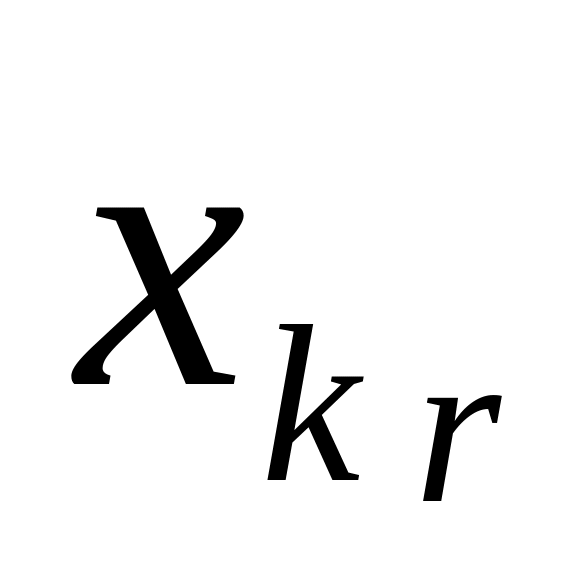
2. Из U удалить ребра

3. Из ГХ удалить ребра , удалить 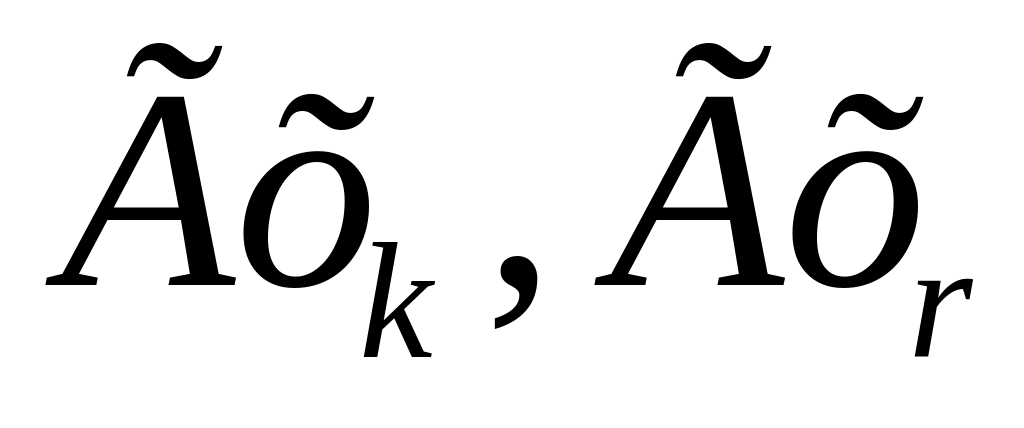, добавить

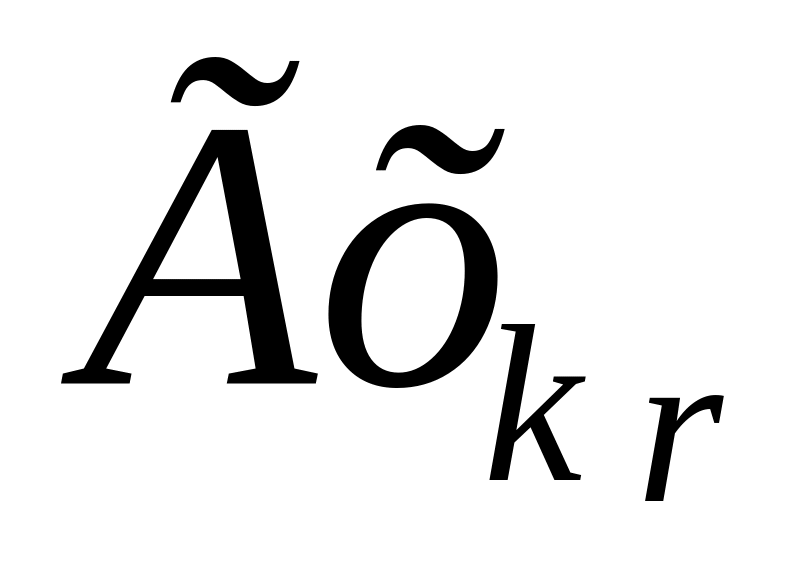
4. Из ГU удалить , удалить , добавить