17. Метод итерационного улучшения

Этот метод реализует частичный, а нередко и упорядоченный перебор решений, генерируя их из некоторых исходных решений в процессе своей работы. Метод относится к классу эвристических. Результатом решения ряда задач структурного синтеза является разбиение некоторого множества на подмножества (например, задача разрезания), либо определяется взаимнооднозначное или однозначное соответствие элементов двух множеств. Примером таких задач может служить задача схемной компоновки – разрезания схемы на подсхемы или позиционирования – размещение микросхем на плате субблока.

Если имеется некоторое исходное решение, то генерация других вариантов может быть выполнена путем допустимых по смыслу задачи перестановок элементов в подмножествах, либо в парах взаимнооднозначных соответствий. Осуществляются те перестановки, которые приводят к улучшению целевой функции с учётом заданных ограничений. Для выбора переставляемых элементов должна существовать некоторая мера. Как правило, хорошей мерой является приращение значения целевой функции, а также может использоваться некоторый критерий, который имеет с ней сильную корреляцию. Перестановки могут быть парными и групповыми. Рассмотрим парные перестановки:

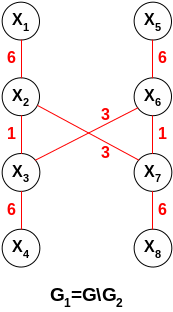
Критерий оптимизации – минимальное количество рёбер, попадающих в разрез.

Если поменять X_i и Х_j, то количество рёбер уменьшится с 3 до 2

Для всех пар необходимо подсчитать F. Выбирается та пара, у которой F0 и максимальна. Процесс заканчивается если:

1. нет F>0,

2. .

3. F

4. K=K_доп -допустимое количество итераций

В ряде случаев количество операций может быть ограничено некоторой константой.

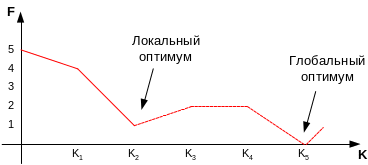
Этот метод гарантирует лишь нахождение локального оптимума. Избежать этого позволяют групповые перестановки. Их идея заключается в следующем: для всех и получаем и выбираем не проверяя условия . Процесс продолжается до тех пор, пока не будут выполнены все парные перестановки. При этом подсчитывается суммарное приращение . Определяется перестановка, для которой P>0 и максимальна. Т.о. определяется группа вершин, принадлежащих Х₁ и вершин, принадлежащих Х₂, для которых и выполняется перестановка.

.

Алгоритм, реализующий итерационный метод, требует гораздо больше машинного времени, чем последовательные, основанные на методе поиска в глубину.

Асимптотическая оценка вычислительной сложности итерационного алгоритма О(n³). Сокращение затрат машинного времени возможно за счёт сокращения числа перестановок. К сокращению перестановок приводит упорядочивание элементов в исходных множествах в соответствии с некоторой мерой. Рассмотрим один из способов упорядочивания:

или подсчитываем величину вклада любого элемента в значение целевой функции. Элементы множества Х упорядочиваются по убыванию вклада подсчитанной оценки. (для другого варианта). Далее в качестве кандидатов на обмен на любом шаге К рассматриваем:

18. Метод параллельно-последовательной свертки. Алгоритм сортировки слиянием. Оценка его вычислительной сложности.

Метод предназначен для объединения элементов множества в некоторые подмножества. Это объединение выполняется в общем случае для элементов, равнозначных для некоторого критерия, в качестве которого может выступать и определенное свойство.

В задачах на графах объединяющими элементами могут быть как вершины, так и ребра. Метод может использоваться, например, для формирования подсхем, т.е. решения задачи схемной компоновки.

Процесс формирования подмножеств данным методом осуществляется следующим образом: до начала свёртки в качестве кандидатов на объединение рассматриваются все элементы множества Х. На первом шаге оценивают соответствие элементов некоторому критерию и выбирают элементы, в наибольшей степени удовлетворяющие ему. В общем случае могут объединятся 2,3 и т.д. элементов. Сформированные подмножества рассматриваются, как элементы нового множества, по отношению к которому процедура может быть повторена. Включение в состав формирующегося множества элементов или частей других подмножеств, как правило, не возможна в соответствии со смыслом задачи. При объединении элементов происходит отсечение других вариантов состава подмножеств, следовательно, точность получаемого решения определяется тем, является ли критерий выбора отсекающей оценкой или оценкой перспективности. В первом варианте решение может быть получено точное, во втором – приближённое.

Возможно два варианта окончания свертки:

1. Свертка заканчивается, когда все вершины объединены в одно подмножество. С практической точки зрения это необходимо, если требуется установить, обладает ли в целом множество некоторым определенным свойством.

2. Требуется выделить подмножество удовлетворяющее некоторым ограничениям. Процесс свёртки заканчивается при удовлетворении всех условий.

Алгоритм сортировки слиянием:

Алгоритм сортировки слиянием является примером точного алгоритма, реализующего метод уравновешенной двоичной свёртки.

Идея алгоритма: попарно сравнивая числа исходного множества (впоследствии это числа, принадлежащие двум разным подмножествам), заносят их в подмножества, состоящие из двух, четырёх и т.д. чисел, записывая, например, сначала меньшее из чисел пары. Алгоритм заканчивает работу, когда исходные числа объединены в одно (новое) множество.

Характерными особенностями реализации метода уравновешенной двоичной свёртки в данном случае являются:

• Критерий слияния подмножеств – их принадлежность одному уровню дерева свёртки; он не связан с целевой функцией, но позволяет построить достаточно эффективную схему сортировки

• Сортировка обеспечивается упорядочиванием элементов каждого подмножества при его получении слиянием двух подмножеств предыдущего уровня

• Окончание процесса свёртки означает реализацию на множестве чисел Х отношения порядка (по возрастанию их значений)

Оценка количества операций сравнения N_c, необходимых для упорядочивания n элементов множества Х алгоритма слияния. Если n – степень двойки, то количество подмножеств (вершин) на уровне и число элементов в них – 2^j-1, где . Число сравнений элементов двух подмножеств уровня будет . Суммарное количество сравнений на уровне j равно:

. Суммируя по j, получим: .

Очевидно, что , в то время как алгоритм сортировки «выбором» (посредством поиска максимального или минимального элемента) требует операций сравнения чисел.