15. Основные способы ветвления при построении дерева решений в методе ветвей и границ.

1. Разбиение множества вариантов на подмножества по методу в ширину и выбор вершины по min(max).

1. Получают все вершины – потомки вершины нулевого уровня (либо часть этих вершин при модификациях метода).

2. Далее на любом уровне выполняется декомпозиция очередного выбранного множества вершин (по минимуму нижней границы или по максимуму верхней).

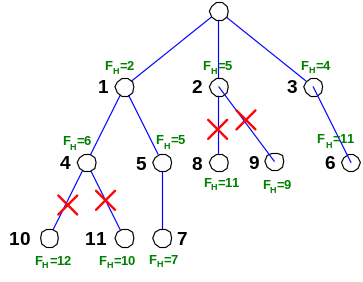
3. Если возможно, выполняется отсечение множества вершин. В ходе построения дерева декомпозиции отсекающая оценка может уточняться.

2. Разбиение множества вариантов по методу поиска в глубину с возвращением – последовательное построение ветвей с заданным порядком их развития.

1. Строится полностью одна ветвь. Получаем опорное решение, значение целевой функции для которого может служить отсекающей оценкой.

2. Далее ветвление выполняется последовательно в заданном направлении.

3. При этом любая ветвь достраивается до конца (если не происходит отсечение).

3. Комбинация декомпозиции в глубину и в ширину

9. Строится одна ветвь по методу в глубину.

10. Далее декомпозиция выполняется по методу в ширину.

11. Оптимальное решение задачи будет найдено, если значение целевой функции для некоторой конечной вершины меньше значения нижней границы для всех «висячих» вершин.

Эффективность того или иного способа ветвления, т.е. степень сокращения перебора зависит от вида задачи и конкретных хар-к графа. От способа ветвления зависит степень сокращения перебора, но дать общих рекомендаций по выбору способа невозможно.

Оптимальное решение задачи будет найдено, если значение целевой функции для некоторой конечной вершины есть min среди всех конечных и меньше значения нижней границы для всех оставшихся «висячих» вершин.

16. Конструирование оценочной функции для верхней и нижней границ целевой функции. (Рассмотрите на примере задачи поиска простой цепи графа).

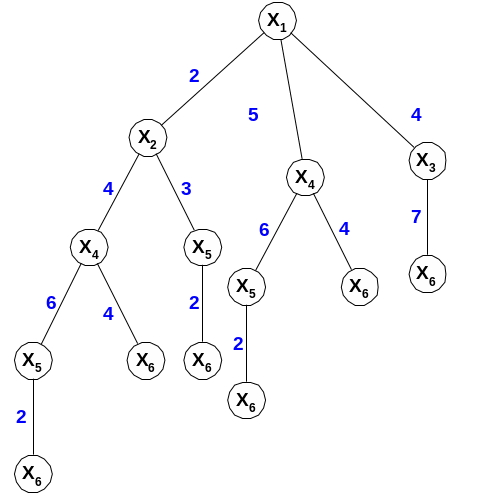
Пример: задача определения маршрута min/max длины в ориентированном графе.

Дерево декомпозиции по методу в ширину:

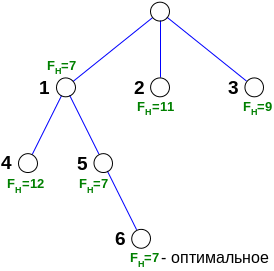
Рассмотрим вариант поиска дерева min длинны. В качестве оценочной функции будем использовать суммарную длину ребер, уже включенных в рассматриваемый фрагмент маршрута. Метод ветвления – поиск в ширину, отсечение – по нижней границе.

Оценочная функция в виде суммы длин ребер, уже включенных в данный фрагмент, является «слабой» - в задаче на минимум такая функция дает минимальное значение нижней границы. Конструирование оценочной функции является сложной задачей. Оно должно базироваться на анализе сущности задачи и св-в нижней или верхней границы. В данном случае сущность задания - последовательное включение ребер в строящийся фрагмент при рассмотренных ранее свойствах функции, которые могут быть использованы в качестве нижних и верхних границ.

Для нижней границы существуют св-ва: не должна уменьшаться

нижняя граница должна быть = F_ц^к (значение ЦФ в конечной вершине)

Рассмотрим для нашей задачи пример конструирования более «сильной» оценочной функции для нижней и верхней границы.

При поиске пути min длинны оценочная ф-ция используемая для вычисления может состоять из 2-х компонент: первой составляющей должна быть сумма длин ребер, уже включенных в данный фрагмент; вторая составляющая – сумма ребер min длинны по всем ветвям решений, порождаемым данной вершиной до ближайшей конечной.

Для верхней границы существуют св-ва: не должна возрастать,

в конечных вершинах она должна быть = F_ц^к (значение ЦФ в конечной вершине).

Для задачи на максимум верхняя граница оценочной функции для любой вершины дерева решений будет не меньше значения целевой функции маршрута максимальной длины, порожденного этой вершиной, если в качестве второй составляющей оценочной функции будет использоваться сумма ребер максимальной длины среди маршрутов для каждого уровня поддерева решений с корнем в этой вершине.

Суммирование необходимо выполнять, начиная от данной вершины до последней конечной.