Аналитические методы теории теплопроводности.

Вывод уравнения теплопроводности.

, где - вектор теплового потока, который направлен в сторону противоположную температуру.

В некотором теле выделим произвольный объем ограниченный замкнутой поверхностью , через которую осуществляется тепловое взаимодействие выделенного объема с окружающей средой – остальной части тела.

Количество тепла, подведенное к телу через поверхность по средствам теплопроводности и полученные за счет действия внутренних источников (стоков) тепла = изменению внутренней энергии выделенного объема.

, - тепло полученное путем теплопроводности, - внутренней теплопроводности.

Сделаем два предположения:

1. Изменение размеров тела вызванное тепловым расширением много меньше размеров тела.

2. Макроскопические частицы тела неподвижны друг относительно друга.

Количество тепла поступившего через элемент площади , за время равное: , полное поступление тепла через поверхность =: . Воспользуемся формулой Астроградского-Гауса , перейдем от объемного интеграла к проекции . Для определение тепла поступившего за счет внутреннего источника введем функцию плотности тепловых источников: . Функция плотности тепловых источников такая функция, когда за время в выделенном поступает тепло: . Согласно первому закону термодинамики изменение внутренней энергии тепла , - интегральная теплоемкость всего тепла, - изменение температур. Изменение температуры . Для того чтобы телу массой сообщить тепло необходимо изменить его внутреннюю энергию или проинтегрировав по всему объему можно найти изменение внутренней энергии тела за время : (1). (2). Прировняем (1) и (2) получим (3), учитывая, что выделенный объем был произвольным в (...) в уравнение (3) д/б =0. Вместо из закона Фурье получим уравнение: (4) –дифференциальное уравнение теплопроводности. Если предположить, что теплофизические свойства среды постоянны, т.е среда в тепловом отношение однородно придем к такому уравнению: (5), где - коэффициент температуропроводности с размерностью . Аналогичный вид имеет уравнение диффузии, где вместо будет коэффициент диффузии, а вместо , концентрация. Коэффициент в отличие коэффициента теплопроводности характеризующего теплопроводящие свойства среды характеризует теплоэнерционые свойства материалов и является мерой скорости выравнивания температурного поля. Оператор Лапласа в правой части (5) характеризует скорость изменения теплового потока и является мерой кривизны изотермической поверхности в некоторой точке. Для этого чтобы найти температурное поле необходимо знать начальное распределение температуры, форму и геометрические размеры тела, а также закон теплового взаимодействия поверхности тела с окружающей средой. Тем самым приходим к постановке краевых задач для уравнения теплопроводности. В предельном случае краевой задаче является задача Коши. Рассматривается уравнение (5) в неограниченном пространстве с начальным условием (6) причем функции и ограничены и непрерывны во всем пространстве. В задаче Коши необходимо найти ограниченные решения уравнения (5) удовлетворяющие условию (6).

Граничные условия: при х=0 , 1-го рода: , 2-го рода: к такому граничному условию приходят когда задан тепловой поток при

, где -интенсивность теплового потока. ; 3-го рода: , т.е задан конвективный теплообмен со средой температура которого окружающей среды. - коэффициент теплообмена.

Единственность решения краевых задач для уравнений параболичес-кого типа.

Рассмотрим ДУ вида: (1), где оператор (конвективный перенос) - отвечает за кондуктивный перенос тепла. Начальные условия: (2). Граничные условия: (3) точка . Краевая задача (1)-(3).

Th: Решение задач (1)-(3) вместе с частными производными 1-го и 2-го порядка по пространственным координатам и частных производных 1-го порядка по времени - единственно.

Д-во: Пусть , не которые решения краевой задачи (1)-(3). Рассмотрим функцию , очевидно если докажем, что , то Th будет доказана. Для доказательства воспользуемся 1-й формулой Грина: . Очевидно, что краевая задача (1)-(3) для функции скорости однородна: . (4). Для 1-й и 2-й краевых задач , интеграл по поверхности будет равен 0. для 3-й краевой задачи можно выразить . Уравнение (4) проинтегрируем по времени получим с учетом……. Для функции : (5) . левая часть (5) не отрицательна, а правая часть не положительна следовательно , т.к - произвольный момент времени, то функция в любой момент времени и в любой точке пространства =0. ( ).

Принцип максимума для уравнения теплопроводности.

Рассмотрим не который объем , ограниченный замкнутой поверхностью и промежуток времени , , к данному условию соответствует область , для двумерной области . представляет собой некий цилиндрический объем с образующими параллельными оси времени

Для одномерной области область будет прямоугольником. Рассмотрим уравнение теплопроводности вида: (1).

Th: Решение уравнения (1) в области достигает наибольшего (наимень-шего) значения либо на нижней границе области (при начальных условиях), либо на боковой поверхности области (в граничных условиях).

Док-во: Рассмотрим доказательство для наибольшего значения, в случае наименьшего значения можно использовать данное доказательство, взяв величины со знаком минус.

Очевидно, в случае доказывать ничего не нужно.

Введем обозначения: - максимальное значение во всем объеме .

-максимальное значение на границе области .

.Предположим, что > . Введем в рассмотрение функцию , где < ( - )/2 , функция во все объеме функции по построению. . Функция непрерывна всюду в области , следовательно, в некоторой точке , она достигает максимума. Эта точка не может принадлежать границе области . Покажем: < < . На боковой поверхности: < < . Следовательно, максимумом функции точки является внутренняя точка области , для этой точке должно выполнятся уравнение теплопроводности (1). , т.к max следовательно , , т.к функции и связаны.

, т.к (max) =0, следовательно, для функции в точке не выполняется уравнение теплопроводности (1) тем самым сделанное предположение о том, что < не верно и = т.е max значение достигается на границе области. Принцип max-ма иллюстрирует простой физический факт, что тепло их более нагретой области распространяется в менее нагретую.

Автомодельное решение уравнений теплопроводности. Функция Грина.

Функцию Грина для уравнения теплопроводности на неограниченной прямой получим с помощью 3-х специально поставленных тепловых задач.

Задача 1: Имеется неограниченный стержень с теплоизомерной боковой поверхностью, часть стержня находиться при температуре , другая часть при температуре . Найти распределение температуры в стержне.

Математическая постановка задачи:

, , (1). (2).

Функцию можно записать . Найдем решение уравнения (1) в классе функций , где - автомодельная переменная, т.е (3), подставим решение вида (3) в (1).

, , подставим в (1) (4),

(4). Чтобы (4) было тождественно относительно переменной необходимо чтобы - параметр автомодельности. Разрешим (4) относительно : , , ,

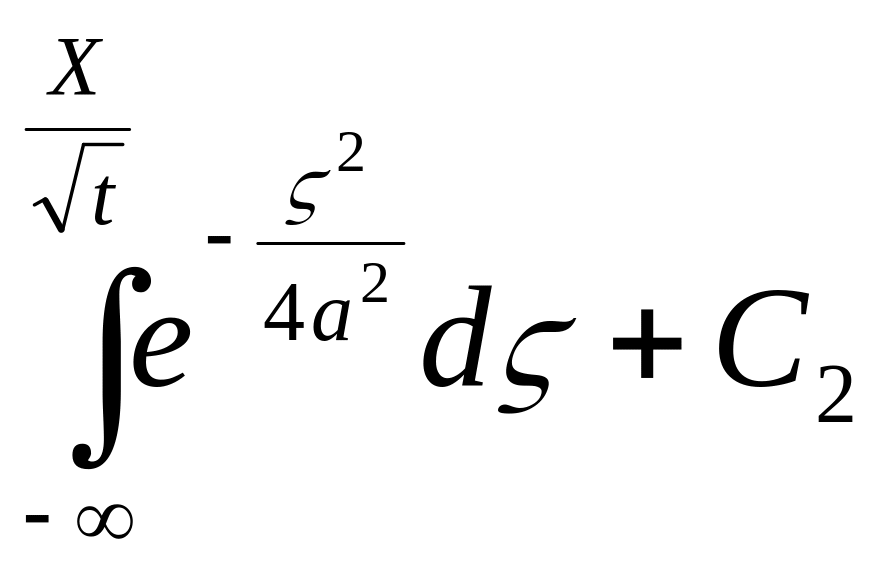, , пусть .

- найденное решение является общим решение уравнения теплопроводности (1). Найдем константы и из начального условия. При , , при , . , . Подставим в общее решение: (5).

Проанализируем решение (5):

Найдем значение в 0: , найдем тепловой поток .

Задача 2. (задача о тепловом импульсе)

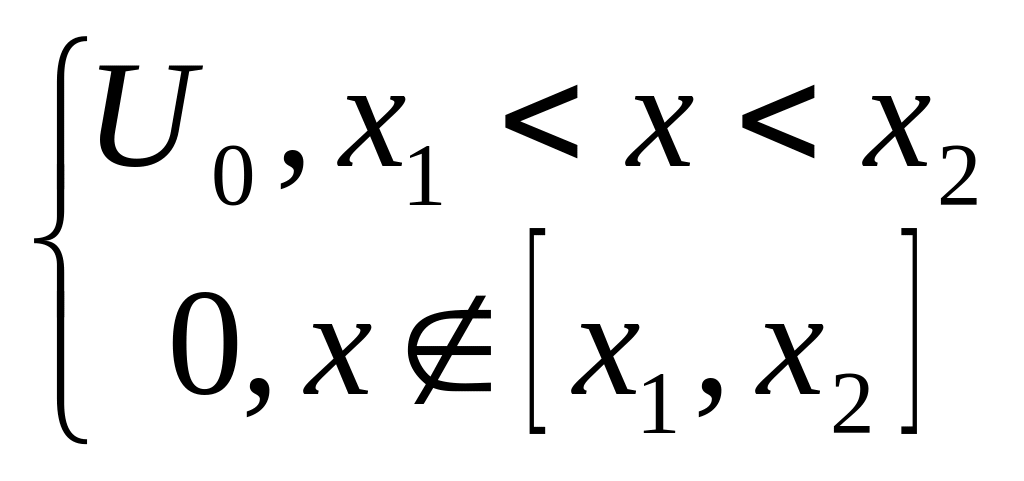, , . , или ,

Количество тепла . Решение задачи №2 легко можно получить из решения задачи №1. Согласно (5) решение задачи о тепловом импульсе имеет вид: (6).

Задача 3. (о точечном тепловом импульсе).

, , . Решение этой задачи можно получить путем предельного перехода из решений предыдущей задачи. Положим в (6): и это означает, что это означает, что источник тепла точечный и единичный. Получим решение:

. Пусть ,

. Найденное выражение является функцией Грина на прямой: (7). Если взять (8). Выражение (8) – фундаментальное решение уравнения теплопроводности.

Функцией Грина для уравнения теплопроводности на прямой называется решение задачи Коши вида , , , .

Решение задачи Коши на бесконечной прямой.

(1), - произвольная кусочная непрерывная прямая.

Для решение задачи (1), дается интеграл следующего вида:

(2), интеграл Пуассона для теплопроводности. Дадим физическую интерпретацию формулы (2) в физической плоскости. задает начальное распределение температуры. Возьмем (произвольную) выделим ей элементарный участок . Предположим, что этому элементарному участку соответствует мгновенный точечный источник тепла . Тепло , а распределение температуры определяется функцией Грина. , очевидно, что действие всех элементарных источников распределенных по оси определяется интегралом. Докажем справедливость (2): Покажем, что функция определяемая выражением (2) действительно является решением задачи 1. кроме этого необходимо показать сходимость интеграла в (2), а т.же интегралов вида: , , . Решение определен-ном (2) подставим в задачу 1: /по определению функции Грина это функция/ /по свойству функции/ , подставим в само уравнение: , функция Грина является решением уравнения теплопроводности . Доказательство сходимости интегралов рассмотрим в предположение, что ограничена не которым значением

в формуле (2). .

жно получить из решения зния теплопроводности (1)000000000000000000000000000000000000000000000000000000000000000000

/ / . Докажем, что

и это интеграл сходиться. / /

, оба интеграла сходятся. Сходимость , доказывается аналогично сходимости производной от интеграла по . отсюда следует сходимость интеграла Пуассона (2) обладает 3-мя следствиями:

Следствие 1. Скорость распространения тепла бесконечна (это свойство решения всех уравнений параболического типа).

Следствие 2. Если функция четная , тогда .

Следствие 3. Если функция не четная .

Решение неоднородного уравнения теплопроводности

на бесконечной прямой.

(1) , где функция - функция плотности тепловых источников, она непрерывна, ограничена.

Решение задачи (1) найдем в виде: (2), где функция является решением задачи: (3), где - параметр.

Решение задачи (3) дается в виде интеграла Пуассона:

, решение задачи (1) имеет вид: (4). Докажем (4):

. , т.к , т.к - решение однородности.

Решение уравнения теплопроводности в полуограниченной области.

(на полупрямой)

Граничные условия первого рода (однородные)

(1).

Для решения (1) воспользуемся следствием 3 из интеграла Пуассона. Для этого функцию продолжим нечетным образом по отрицательной части, прямой. - можно записать интеграл Пуассона:

- / / ( ) , в (…) , - функция Грина 1-ой краевой задачи.

( - ); - .

Решение задачи (1): (2). Рассмотрим задачу: имеется стержень, температура стержня = , боковая поверхность теплоизоли-рована. Температура на левой границе =0. Подставим значение .

- ) / / (

) .
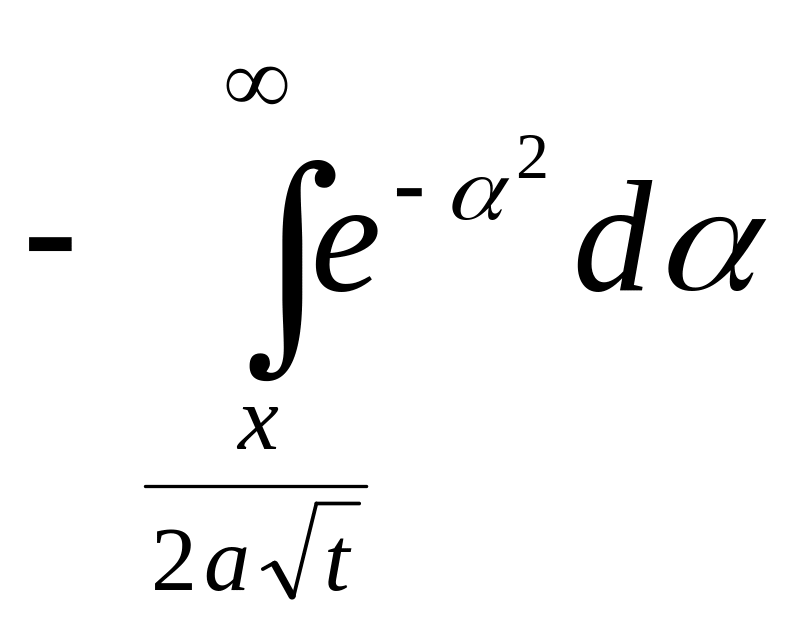