2. Способи оцінки рівня ризику

Управління ризиком означає поетапне здійснення визначених операцій, а саме: ідентифікації ризику; кількісної оцінки рівня ризику; розробки стратегії і тактики управління ризиком; здійснення конкретних процедур з управління ризиком. Кожен етап передбачає виконання декількох операцій. Перший етап процесу управління ризиками - ідентифікація ризику - найбільш складний. Він вимагає глибокого якісного аналізу, що припускає наступні процедури: виявлення джерел (причин) ризику; визначення і класифікація можливих для того чи іншого напрямку діяльності (або проекту) типів ризику; вибір критеріїв і параметрів для оцінки кожного типу ризику; визначення граничних умов для оцінки прийнятного рівня

ризику; встановлення зон підвищеного ризику; визначення послідовність (за часом) виникнення різних типів ризику і прив'язка її до календарними планами виробничо-господарської діяльності (або здійснення конкретного проекту); оцінка ймовірності виникнення різних типів ризику.

Другий етап - кількісна оцінка рівня ризику – доповнює якісний аналіз. При цьому чисельно визначають розміри окремих ризиків і сумарного ризику того чи іншого напрямку діяльності (або проекту). Ризик визначають в абсолютному вимірі як величину прогнозованих втрат (збитків) і у відносному - як величину втрат, віднесену до визначеної бази. Базу вибирають менеджери в Залежно від специфіки підприємства і виду конкретного ризику; це можуть бути прибуток, витрати на виробництво, вартість активів, втрати минулих років і т. д. Для кількісної оцінки рівня ризику можна використовувати наступні методи: Статистика та експертних оцінок. Коротко викладемо суть цих методів.

Статистичний метод менеджери використовують за наявності значно обсягу статистичної інформації про реалізацію визначених видів ризику і втрат від них в минулі періоди по кон-

конкретними напрямками підприємницької діяльності в цілях оцінки ймовірності їх настання в майбутньому. Ця ймовірність і буде ступенем ризику, вона виражається величиною середньоквадратичного відхилення від очікуваних величин. Головні елементи статистичного методу - математичне сподівання, дисперсія, середньоквадратичне відхилення, коефіцієнт варіації.

Математичне сподівання (Еr) - це сума добутків всіх можливих значень, які може приймати досліджуваний параметр (Е), на вірогідність їх виникнення. Математичне сподівання приблизно дорівнює середньому арифметичному можливих значень розглянутого параметра. Дисперсія - це міра відхилення (розкиду) фактичного значення ознаки Е від його середнього значення, яку визначають як квадрат відхилення значень ознаки від його середнього значення, множений на ймовірність Рi. У теорії ймовірностей дисперсію визначають як математичне сподівання квадрата відхилення:

Середньоквадратичне відхилення (σ) розраховується витягом квадратного кореня з дисперсії і показує максимально можливе відхилення параметра від його Середньоочікувана значення:

Величина середньоквадратичного відхилення характеризує степінь конкретного ризику - чим вона більша, тим ризикованіше обраний шлях.

Коефіцієнт варіації - це відношення середньоквадратичного відхилення до математичного сподівання . Чим менше коефіціент варіації, тим більш стабільна прогнозована ситуація і менше рівень ризику. Проілюструємо розрахунок наведених показників.

Приклад. [21, 97-99]. Фірма повинна вибрати одне з двох направлений свого розвитку. Перший напрямок вимагає єдино разових інвестицій у розмірі 100 тис. ден. од. Враховуючи відбуваються на ринку зміни, можливі чотири варіанти ситуацій. У випадку першого варіанту фірма може отримати прибуток від вкладеного капіталу в розмірі 40%; другий і третій варіанти однакові за результатами, а відрізняються лише деякими специфічними осо-

бенностями, пов'язаними з рекламою; встановлено, що фірма може отримати прибуток від вкладеного капіталу в розмірі 10%; четвертий - фірма може зазнати збитків - 20% вкладеного капіталу. Другий напрямок розвитку фірми вимагає такого ж обсягу інвестицій, як і перше; при цьому також можуть виникнути чотири варіанти ситуацій: перший - фірма отримує 70% прибутку від вкладеного капіталу; другий і третій - по 10%; четвертий – фірма втрачає 50% вкладеного капіталу.

Рішення. При першому напрямку розвитку фірма має ймовірність 1 з 4 (чи 0,25), що вона отримає 40% прибутку; 2 з 4 (чи 0,5) - 10% прибутку; 1 з 4 (0,25) - втратить 20%. Таким чином, математичне сподівання (середнє значення відсотка прибутку) для цього напрямку розвитку з урахуванням ймовірності складе 10%, тобто

= 0,25. 40 + 0,5. 10 + 0,25. (- 20) = 10%.

Для другого напрямку розвитку фірми

= 0,25. 70 + 0,5. 10 + 0,25. (- 50) = 10%. Таким чином, математичне сподівання для обох напрямів однаково. З табл. 9.1 видно, що для першого напряму дисперсія дорівнює 450, середньоквадратичне відхилення коефіцієнт варіації 21/10 = 2,1; для другого напрямку дисперсія дорівнює 1800, середньоквадратичне відхилення коефіцієнта варіації 42/10 = 4,2

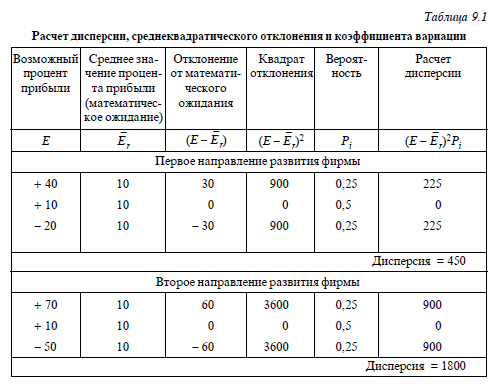
Якби розвиток фірми було повністю визначеним, тобто 100% гарантії виконання, то відхилення від очікуваного прибутку і середньоквадратичне відхилення також дорівнювали б нулю. При першому напрямку розвитку ризик становить 21 одиницю, а коефіціент варіації - 2,1, при другому напрямку – відповідно 42 і 4,2, що вдвічі більше, ніж для першого напряму. значить, другий напрямок в 2 рази ризикованіше. При нестачі або відсутності статистичної інформації доводиться застосовувати метод експертних оцінок, який зводиться до збору і обробки думок досвідчених експертів, які дають бальну оцінку ймовірності виникнення того чи іншого виду ризику і степені втрат. У практиці доцільно комбінувати статистичний та експертний методи оцінки рівня ризику.