Тема 7. Управління інвестиційним портфелем підприємства

1. Склад інвестиційного портфеля

Підприємства здійснюють інвестиційну діяльність в різних формах і напрямках відповідно до їх інвестиційною політикою. В залежності від пріоритетів інвестиційної політики підприємства формують відповідний портфель інвестицій і його структуру.

Інвестиційний портфель - це сукупність інвестиційних інструментів, що забезпечують здійснення стратегії розвитку підприємства, отримання додаткового прибутку, диверсифікацію вкладень капіталу. Інвестиційний портфель може включати наступні види капіталовкладень: • реальні інвестиції (капіталовкладення) в основні фонди і нематеріальні активи для розвитку та вдосконалення

виробничій діяльності підприємства; • фінансові інвестиції в різні види фінансових активів; в залежності від характеру вкладень вони поділяються на прямі і портфельні. Прямі інвестиції - внесення коштів або майна до статутного фонду іншого підприємства для набуття корпоративних прав. Портфельні інвестиції - придбання різних видів цінних паперів на фінансовому ринку. По періоду інвестування розрізняють коротко-та довгострокові інвестиції. Короткострокові інвестиції характеризуються вкладенням капіталу на період не більше одного року (наприклад, придбання

цінних паперів зі строком погашення до одного року). Довгострокові інвестиції - вкладення капіталу на період більше одного року (наприклад, капіталовкладення, вклади в статутні фонди інших підприємств, придбання цінних паперів з терміном погашення більше одного року).

2. Інвестиційні операції та зміни вартості грошей в часі

Інвестуючи капітал, фінансові менеджери планують не тільки повернути вкладені кошти, але й отримати дохід. При цьому слід враховувати, що гроші з часом знецінюються; ризик і невизначеність, пов'язані з вкладенням капіталу, зростають у міру віддалення періоду отримання доходу від моменту інвестування. Тому у фінансовому менеджменті (особливо для оцінки інвестиційних операцій) використовують обчислення, що дозволяють враховуються зміна вартості грошей у часі. В їх основі лежать розрахунки нарощування вартості інвестованого капіталу при різних особистих схемах нарахування простих і складних відсотків; приведеної (нинішньої) вартості капіталу шляхом математичного та банківського дисконтування; нарощеної і наведеної вартості потоку однакових платежів через рівні проміжки часу (Постійних ануїтетів); процентної ставки, що забезпечує реальну прибутковість фінансових операцій з урахуванням інфляції та ін

У навчальній літературі багато уваги приділяється методам фінансових розрахунків з урахуванням впливу фактора часу на вартість грошей. Розглянемо базові формули, що використовуються в цих розрахунках. Почнемо з найпростішої фінансової операції - однократних вкладених сум капіталу PV (Present Value - теперішня вартість) з умовою, що через час Т нарощена сума FV (Future Value - майбутня- вартість) буде повернена. Для визначення ефективності такого вкладення капіталу використовують дві величини: відносний ний ріст (процентну ставку)

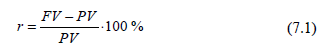
і відносну знижку (дисконт) - облікову ставку

які характеризують приріст капіталу, віднесене або до початкового внеску, або до кінцевої сумі. Ці величини взаємопов'язані:

В залежності від способу нарахування відсотки діляться на прості і складні. Як відомо, при використанні простих відсотків їх сума протягом усього терміну операції нараховується виходячи з першочергово вкладеного капіталу незалежно від кількості періодів нарахування та їх тривалості. При цьому суму відсотків (S) визначають за формулою

де r - річна ставка відсотків; T - тривалість фінансової операції, років.

В кінці терміну угоди сума з відсотками складе

При нарахуванні складних відсотків початковий капітал збільшується разом з відсотками. Таким чином, база для нарахування складних відсотків (на відміну від простих) буде збільшується з кожним періодом нарахування. Нарощена сума з відсотками в кінці терміну операції, яка тривала Т років, із щорічним нарахуванням складних відсотків за ставкою r складе

Зазвичай в короткострокових операціях (до одного року) дохід нараховується за формулою простих відсотків, а при вкладеннях капітала на термін більше одного року можна використовувати формулу складних відсотків. Іноді (наприклад, при високому темпі інфляції), щоб зацікавити інвесторів, позичальник може запропонувати виплату доходу за схемою нарахування складних відсотків декілька разів на рік. У цьому випадку нарощену суму визначають за формулою

де r - річна ставка складних відсотків; m - кількість нарахованих відсотків за рік. Можна використовувати також формулу перерахунку кілька разів в рік за річною ставкою облікового відсотка d:

Якщо тривалість операції перевищує один рік, але назчитує нецілу кількість років, можна застосовувати комбіновану схему нарахування доходу: складні відсотки - за цілу кількість

років, прості - за неповну частину року. При цьому нарощену суму визначають за формулою

де [T] - ціла кількість років; t = T - [T] - дробова частина числа (неповна частина року).

При випуску цінних паперів, укладенні фінансових контрактів, позиках, як правило, вказують річну відсоткову або дисконтну ставку і обумовлюють умови нарахування доходу (по простим процентам, складним, комбінованою схемою, нарахування складних відсотків або дисконтування кілька разів на рік). Знаючи річну відсоткову або дисконтну ставку, можна визначити нарощену вартість при короткострокових фінансових вкладеннях (на термін менше одного року). Для цього треба встановити тривалість фінансової операції та умови розрахунків - звичайний або точний відсоток; при цьому день видачі та погашення кредита вважається як один день.

При розрахунку звичайного (комерційного) відсотка в якості тимчасової бази беруть умовний рік, що дорівнює 360 дням (12 місяців по 30 днів). Звідси при тривалості фінансової операції t днів і річній процентній ставці r звичайний відсоток

а нарощена сума

Аналогічно при використанні річної облікової ставки d отримуємо

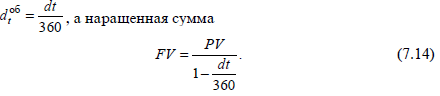
Точний відсоток одержують, коли в якості тимчасової бази беруть фактичну кількість днів у році (365 або 366). Звідси при тривалості короткострокових фінансових вкладень t днів і

річній процентній ставці r точний відсоток

, а нарощена сума

При використанні річної ставки d отримуємо

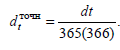
При цьому нарощена сума

Якщо потрібно вирішити зворотну задачу, тобто знаючи нарощену вартість (або ціну погашення боргового зобов'язання - облігації, векселі, сертифіката), визначити нинішню (приведену) вартість нарощеного капіталу, використовують дисконтування. В заленості від виду ставки (процентна або облікова) розрізняють матемтичні дисконтування і банківський (комерційний) облік. Наведемо формули для математичного дисконтування: • при нарахуванні доходу за формулою простих відсотків

• при нарахуванні доходу за формулою складних відсотків

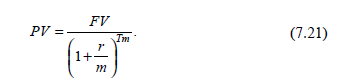
Математичне дисконтування використовують в методиках оцінки ефективності інвестиційних проектів, що враховують вплив фактора часу на майбутні грошові потоки. Ці методики передбачає розрахунок певних показників. Розглянемо їх.

Грошовий потік - це різниця між усіма грошовими поступлень за певний період і грошовими витратами підприємства за цей же період, тобто сума чистого прибутку й амортизації.

Дисконтна ставка - це процентна ставка (r), використовувана для розрахунків наведеної (нинішньої) вартості майбутніх грошових потоків.

Коефіцієнти дисконтування - це понижуючі коефіцієнтів, використовувані в розрахунку наведеної (нинішньої) вартості майбутніх доходів

Дисконтований грошовий потік - це вартість на сьогоднішній день майбутніх доходів з урахуванням втрати частини вартості грошей з часом:

Чиста теперішня (приведена) вартість проекту (NPV – Net Present Value) - це різниця між дисконтованою (нинішньої) вартістю майбутніх грошових потоків (PV) та первісними

інвестиціями по проекту. Якщо NPV позитивна, проект є економічно прийнятною мим, якщо негативна - проект невигідний для інвесторів, так як у цьому випадку майбутні доходи (з урахуванням їх знецінення у часі не відшкодовують первісних інвестицій.

Приклад. Визначити NPV інвестиційного проекту, якщо доходи будуть надходити в сумі 10, 30 і 35 тис. ден. од. відповідно через 3, 4 і 5 років. Початкові інвестиції - 50 тис. ден. од.; дисконтна ставка - 15%.

Рішення. Визначаємо дисконтну вартість майбутніх доходів:

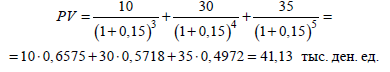
Тоді NPV = 41,13 - 50 = - 8,87 тис. ден. од. Отже, інвенстувати такий проект невигідно.

Наведемо формули банківського (комерційного) обліку, які застосовують в банківських розрахунках, пов'язаних з купівлею (обліком) векселів або інших короткострокових обов'язань:

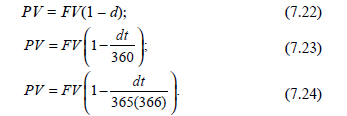
Приклад. Вексель на 100 тис. ден. од. містить зобов'язання про виплаті цієї суми 15 квітня поточного року. Держатель векселя пред'являє його банку достроково - 1 березня. Банк погодився врахувати вексель з дисконтом 50% річних. Яку суму отримав пред'явитель векселя?

Рішення. При використанні звичайного (комерційного) відсотка пред'явник векселя отримає суму

При використанні точного відсотку пред'явник векселя отримає суму

Часто інвестиції пов'язані з тією чи іншою періодичністю платежів, при яких суми грошей можуть неодноразово переміщатися між сторонами угоди, тобто доводиться мати справу з потоками односторонніх або зустрічних платежів. Якщо передбачаються внески (виплати) однакових сум через рівні проміжки часу протягом певного періоду, то такі платежі називаються постійної фінансової рентою, або постійним ануїтетом. Прикладами ануїтету є виплата фіксованих дивідендів по привілейованих акціях, нарахування амортизації линів-

вим методом (в даний час в Україні цей метод використовують для нематеріальних активів) та ін Якщо період виплати ануїтету не визначений, такі платежі називають вічним ануїтетом (або довічної фінансової рентою); прикладами можуть бути фіксовані дивіденди за привілейованими акціями, фіксована сума пенсії.

Розрізняють такі ануїтети: пренумерандо (якщо платежі здійснюються на початку кожного часового інтервалу) і постнумерандо, або звичайні ануїтети (якщо платежі здійснюються в кінці кожного інтервалу, їх найчастіше використовують у інвестиційних розрахунках).

Розрізняють такі поняття, як нарощена (майбутня) вартість ануїтету і приведена (нинішня) вартість ануїтету.

Нарощену (майбутню) вартість FV від щорічних платежів однакового розміру А визначають за формулою

де Kr, n - акумулюючий коефіцієнт нарощення при заданій річній відсоткової ставки r та кількості років n,

Нарощену суму ануїтету визначають шляхом приведення всіх платежів з урахуванням її збільшення до моменту останнього платежу.

Приведення щорічних платежів до вихідного моменту (першому платежем) з урахуванням дисконтування платежів, здійснюваних в майбутньому, дозволяє визначити наведену (нинішню) вартість ануїтету

де Kr ', n - акумулюючий коефіцієнт дисконтування при заданої річної відсоткової ставки r та кількості років n,

Приклад. Позичальник взяв кредит на 3 роки під 20% річних. Кредит повинен бути погашений трьома рівними платежами по 15 тис. ден. од. в кінці кожного року. Яка сума кредиту?

Рішення. Сума виданого кредиту - це теперішня вартість ануїтету в 15 тис. ден. од. Знаходимо її за формулою (7.27):

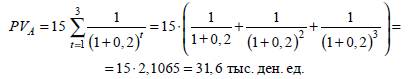
Наведену вартість вічного ануїтету розраховують за формулою

де А - вічний ануїтет, тобто фіксована сума, регулярно виплачується невизначено довго.

Приклад. Річний фіксований дивіденд по привілейованої акції дорівнює 60 грош. од. Знайти вартість цієї акції (приведену вартість вічної ренти), якщо дисконтна ставка становить 20%.

Рішення. По формуле (7.29) знаходимо

Для визначення коефіцієнтів нарощення і дисконтування, а також акумулюючих коефіцієнтів нарощення і дисконтування ануїтетів існують таблиці, якими зручно користуватися для практичних розрахунків (наводяться в підручниках з фінансового менеджменту).