Глава 8

8.1.Какая задача оптимизации называется задачей линейного программирования?

Задачами линейного программирования называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств и неравенств.

8.2. Дать определение общей задачи линейного программирования.

8.3. Дать определение канонической задачи линейного программирования.

8.4.Описать алгоритм сведения общей задачи к задаче в канонической форме линейного программирования. Привести пример.

Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно в общем случае уметь, во-первых, сводить задачу минимизации функции к задаче максимизации; во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам; в-третьих, заменять переменные, которые не подчинены условиям неотрицательности.

Нестрогое ограничение-неравенство общей задачи линейного программирования можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство

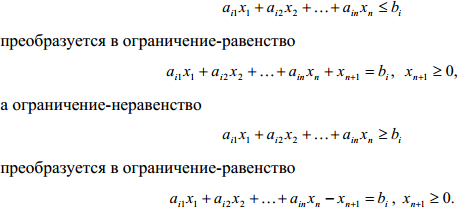
Вводимые дополнительные переменные имеют вполне определенный смысл в рамках решения экономических задач. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, как это будет показано в дальнейших примерах, равно объему неиспользуемого соответствующего ресурса.

8.5. Какие задачи линейного программирования можно решить графически?

Материал из Wiki:

Задачи линейного программирования, заданные в двумерном пространстве, то есть ограничения содержат две переменные.

8.6. Описать алгоритм графического решения задачи линейного программирования.

Материал из Wiki:

Пусть задача линейного программирования задана в двумерном пространстве, то есть ограничения содержат две переменные.

Найти минимальное значение функции

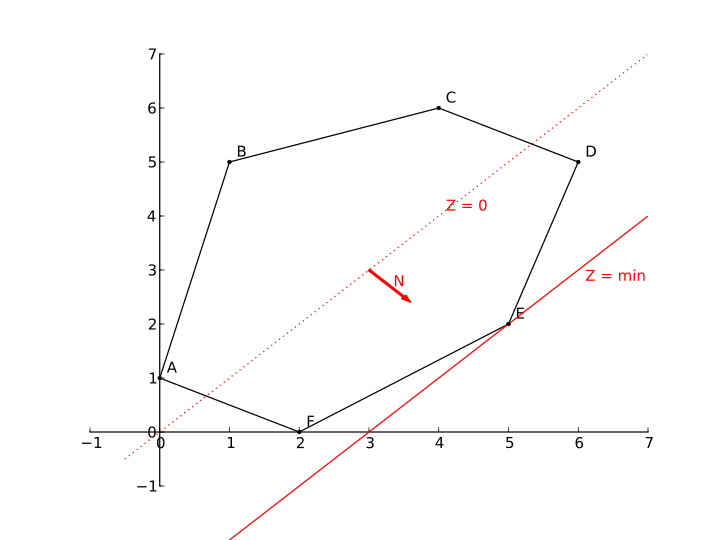
Если же многоугольник решений представляет собой неограниченную многоугольную область, то возможны два случая.

Случай 2. Прямая, передвигаясь, всё же становится опорной относительно многоугольника решений. Тогда в зависимости от вида области линейная функция может быть ограниченной сверху и неограниченной снизу, ограниченной снизу и неограниченной сверху, либо ограниченной как снизу, так и сверху.

Или конкретный пример из учебника:

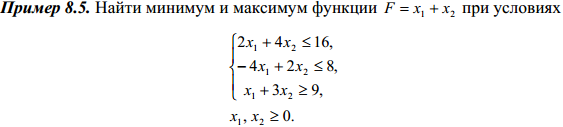
Построим многоугольник решений. Для этого в неравенствах системы ограничений и в условиях неотрицательности переменных следует заменить знаки неравенств знаками точных равенств. Построив полученные прямые, найдем соответствующие полуплоскости и их пересечение (рис. 8.2).

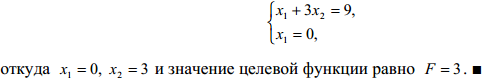
8.7. Дать определение плана и оптимального плана задачи линейного программирования.

8.8. Какую задачу линейного программирования можно решить с помощью симплекс-метода?

Симплекс-метод основан на направленном переходе от одного опорного плана к другому, при котором значение целевой функции возрастает. Такой переход возможен, если уже известен какой-нибудь исходный опорный план.

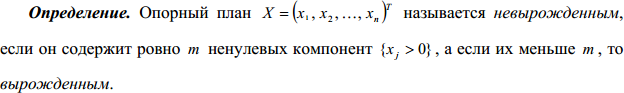
Нахождение решения симплекс-методом гарантируется только в том случае, когда на каждом шаге рассматриваемый опорный план является невырожденным. В противном случае задача линейного программирования называется вырожденной, возможны холостые шаги симплекс-метода, т.е. шаги, в результате которых значение целевой функции не изменяется. При этом теоретически возможно и зацикливание, т.е. бесконечное повторение холостых шагов.

8.9. Дать определение опорного плана задачи линейного программирования.

8.10. Сформулировать признак оптимальности опорного плана для задачи линейного программирования симплексным методом.

8.11. Показать, что если для некоторого Δk < 0 среди чисел нет положительных, то целевая функция задачи линейного программирования в канонической форме (8.15) − (8.17) не ограничена на множестве ее планов.

8.15. В каких случаях для решения задачи линейного программирования необходимо добавлять искусственные переменные?

Для задачи линейного программирования, записанной в форме канонической, можно непосредственно указать ее опорный план только в том случае, если среди Pj векторов имеется m единичных. Когда это не выполняется, то следует применять метод искусственного базиса.

8.16. Показать, что для метода искусственного базиса величины и kF0jΔ зависят от параметра M

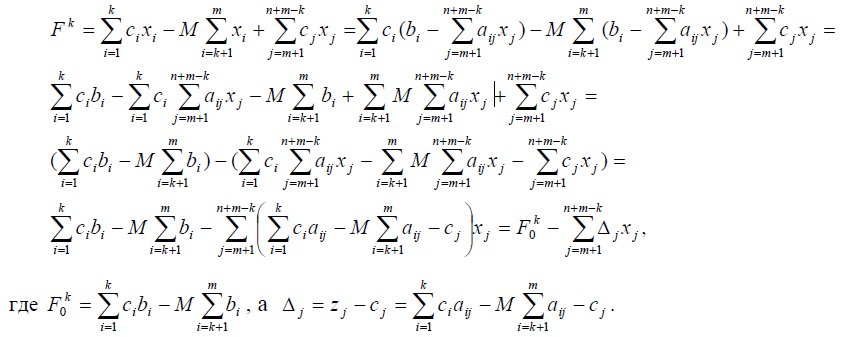
Таким образом, и состоят каждая из двух независимых частей, одна из которых зависит от параметра M, а другая − нет.

8.17. В каких случаях метод искусственного базиса не даст решения задачи линейного программирования?

Если достигнуто оптимальное решение, где хотя бы одна искусственная переменная входит в базис, то задача не имеет допустимых решений.

Если в M-задаче F(целевая функция) стремится в бесконечность, то исходная задача не имеет решений. Это происходит из-за пустой области допустимых решений или из-за того, что F также стремится в бесконечность.

Если в оптимальном решении М-задачи хотя бы одна искусственная переменная не равна 0, то исходная ЗЛП не имеет решения в силу несовместимости ограничений.