6.12 В чём состоит стратегия метода Хука-Дживса?

Эффективность прямого поиска точки минимума ограниченной снизу целевой функции можно повысить, если на каждом k-ом шаге поиска последовательно выбирать направление спуска. Для этого на каждом k-ом шаге выделяют предварительный этап исследующего поиска. Целью этого этапа является выбор направления спуска путём исследования поведения целевой функции f(x) в окрестности точки x^k-1, найденной на предыдущем шаге. В результате исследующего поиска находится точка , для которой f( <f(x^k-1). Направление спуска, завершающего k-й шаг поиска, определяется вектором . Такая стратегия поиска, предложенная в 1961г., получила название метод Хука-Дживса. Это один из наиболее эффективных прямых методов.

6.13. Какие методы для реализации исследующего поиска в методе Хука-Дживса Вы знаете? В чём состоит метод исследующего покоординатного поиска?

Алгоритм метода Хука-Дживса на каждом шаге содержит две основные процедуры:

а) исследующий поиск в окрестности данной точки x для определения направления убывания функции f(x). В результате получим точку ;

б) перемещение в направлении убывания ( ).

Поиск завершается, если после шага «а» получено, что .

6.14. Перечислите способы выбора ускоряющего множителя в методе Хука-Дживса при перемещении в направлении убывания.

6.15. Какие алгоритмы случайного поиска Вы знаете?

6.16. От какого параметра в наибольшей степени зависит эффективность алгоритмов случайного поиска?

От выбора величины шага α.

6.17. На основе собственного опыта дать сравнительный анализ прямых методов.

Прямые методы:

Минимизация функций по правильному (регулярному) симплекс

Минимизация функций при помощи нерегулярного симплекса

Метод циклического покоординатного спуска

Метод Хука – Дживса

Методы случайного поиска

Глава 7

7.1. Что называется обобщенной (классической) функцией Лагранжа задачи условного экстремума?

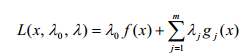- обобщенная функция Лагранжа

- множители Лагранжа

- классическая функция Лагранжа

7.2. Что называется градиентом обобщенной (классической) функции Лагранжа?

Градиентами обобщенной и классической функций Лагранжа по x называются вектор-столбцы, составленные из соответствующих частных производных первого порядка по Xi, i=1,.., n:

7.3. Что называется вторым дифференциалом обобщенной (классической) функции Лагранжа?

Вторым дифференциалом обобщенной (классической) функции Лагранжа называется функция

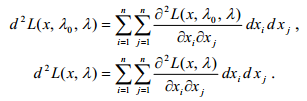
7.4. Что называется первым дифференциалом ограничения gj(x)?

Первым дифференциалом ограничения gj(x) называется функция

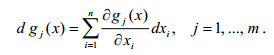
7.5. Когда ограничение gj(x)<=0 называется активным в точке x*?

Если

7.6. Когда ограничение gj(x)<=0 называется пассивным в точке x*?

Если

7.7. При каких условиях градиенты ограничений g1(x),…, gm(x) называются линейно зависимыми в точке x*, линейно независимыми в точке x*?

Градиенты ограничений называются линейно независимыми в точке x*, если равенство выполняется только при Если существуют числа одновременно не равные нулю, для которых равенство выполняется, то градиенты линейно зависимы.

7.8. Сформулировать необходимые условия экстремума первого порядка с ограничениями типа равенств.

Необходимые условия минимума (максимума) первого порядка. Пусть x* − точка локального минимума (максимума) в задаче .

Тогда найдется такое число , и вектор , не равные одновременно нулю и такие, что выполняются следующие условия:

− стационарности обобщенной функции Лагранжа по x

(7.12a)

− допустимости решения

(7.12б)

− неотрицательности для условного минимума

(7.12в)

(условие неположительности для условного максимума );

− дополняющей нежесткости

(7.12г)

Если при этом градиенты активных в точке x* ограничений линейно независимы (выполняется условие регулярности), то Точки x*, удовлетворяющие системе (7.12), называются условно-стационарными.

7.9. Какие точки x* называются условно-стационарными в задаче экстремума с ограничениями типа равенств?

(является продолжением/входит также в 7.8)

Если при этом градиенты активных в точке x* ограничений линейно независимы (выполняется условие регулярности), то Точки x*, удовлетворяющие системе (7.12), называются условно-стационарными.

7.10. Какие точки экстремума x* называются регулярными, а какие − нерегулярными при ограничениях типа равенств?

Определение. Точка экстремума, удовлетворяющая системе (7.7) при λ^*₀ ≠ 0 называется регулярной, а при

λ^*₀ = 0 − нерегулярной.

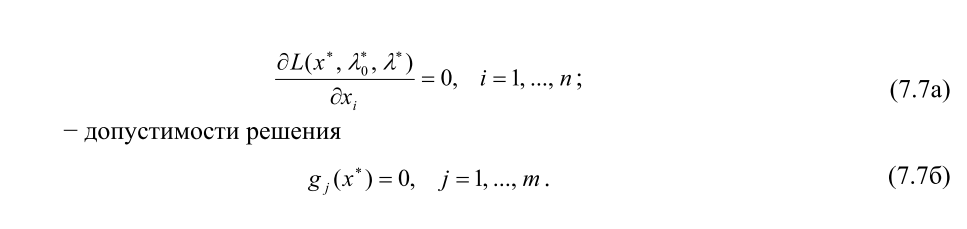
7.11. В каком случае антиградиент целевой функции является линейной комбинацией градиентов ограничений?

Условие в регулярной точке экстремума x* отражает тот факт, что антиградиент целевой функции является неотрицательной (положительной в случае максимума) линейной комбинацией градиентов функций, образующих активные ограничения в точке x*. Действительно, условие

с учетом условия можно переписать в виде:

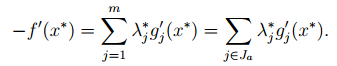
7.12. Сформулировать необходимые условия экстремума второго порядка; достаточные условия экстремума в случае ограничений типа равенств.

Необходимые условия экстремума второго порядка. Пусть x^* − регулярная точка минимума (максимума) в задаче (7.1) и имеется решение (x^*, λ^*) системы (7.8). Тогда второй дифференциал классической функции Лагранжа, вычисленный

в точке (x^*, λ^*) , неотрицателен (неположителен):

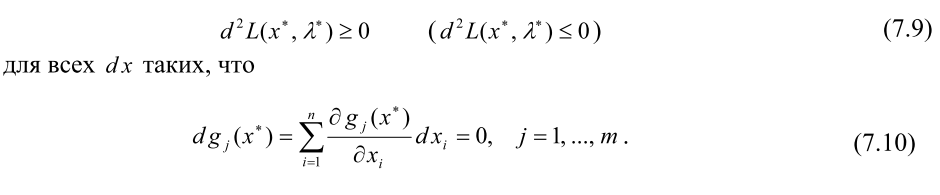
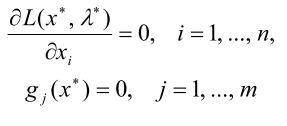
7.13. В каких точках x* проверяются необходимые условия второго порядка и достаточные условия в случае ограничений типа равенств?

В условно-стационарных точках.

7.14. Сформулировать алгоритм решения задачи нахождения экстремума в случае ограничений типа равенств.

Шаг 1. Составить обобщенную функцию Лагранжа

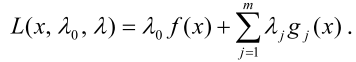
Шаг 2. Записать необходимые условия экстремума первого порядка

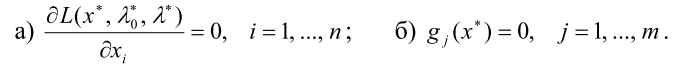
Шаг 3. Решить систему для двух случаев

Шаг 4. Для выделенных на шаге 3 точек проверить достаточные условия

экстремума:

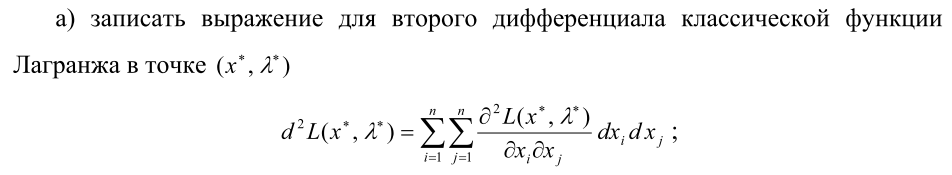
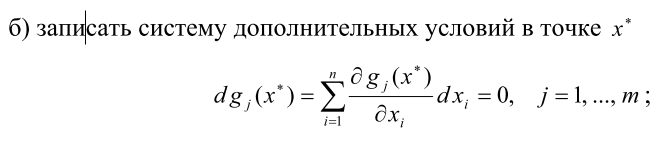
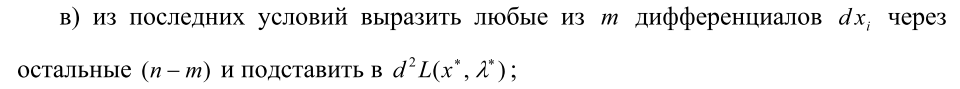
Шаг 5. Вычислить значения функции в точках условного экстремума.

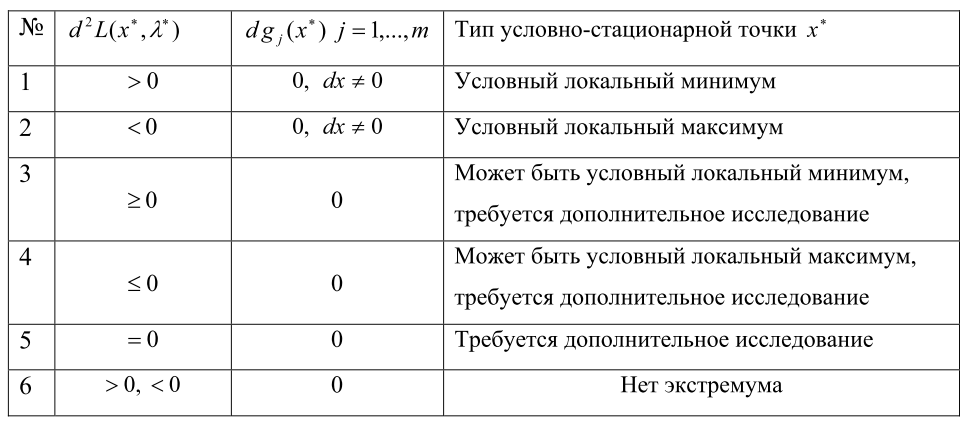
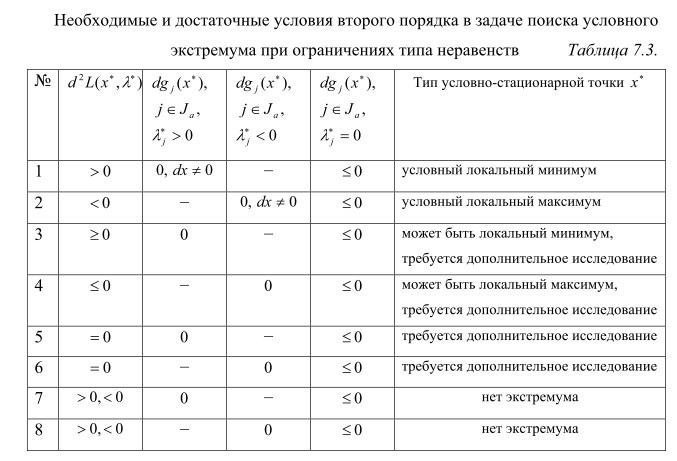
7. 15. Сформулировать необходимые условия минимума (максимума) первого порядка с ограничениями типа неравенств.

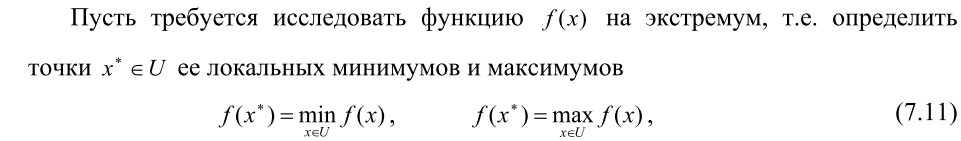
7.16. В каком случае необходимые условия минимума (максимума) первого порядка с ограничениями типа неравенств являются одновременно и достаточными условиями минимума (максимума)?

7.17. Сформулировать достаточные условия минимума (максимума) первого порядка в случае ограничений типа неравенств.

7.18. Сформулировать необходимое условие минимума (максимума) второго порядка в случае ограничений типа неравенств.

7.19. Сформулировать достаточные условия экстремума второго порядка в случае ограничений типа неравенств.

7. 20. Сформулировать алгоритм решения задачи нахождения экстремума в случае ограничений типа неравенств.

Шаг 1. Составить обобщенную функцию Лагранжа

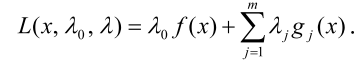
Шаг 2. Записать необходимые условия минимума (максимума) первого порядка

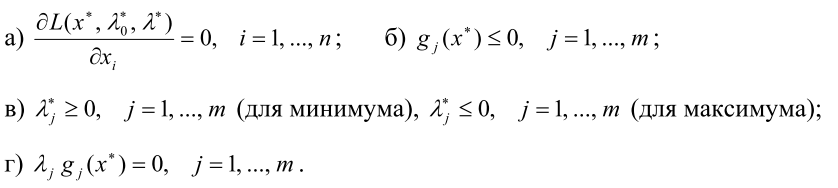
Шаг 3. Решить систему для двух случаев

Шаг 4. Для выделенных на шаге 3 точек проверить достаточные условия экстремума первого или второго порядка.

Шаг 5 

Шаг 5. Вычислить значения функции в точках условного экстремума.