Глава 6

6.1. Сформулировать стратегию построения алгоритма симплексного поиска.

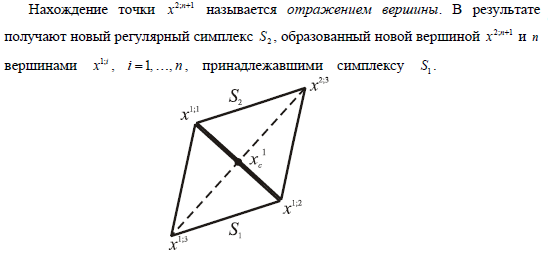
6.2. Какая нумерация вершин симплекса называется правильной?

Нумерацию вершин симплекса S_k назовем правильной, если выполнено неравенство

Пример

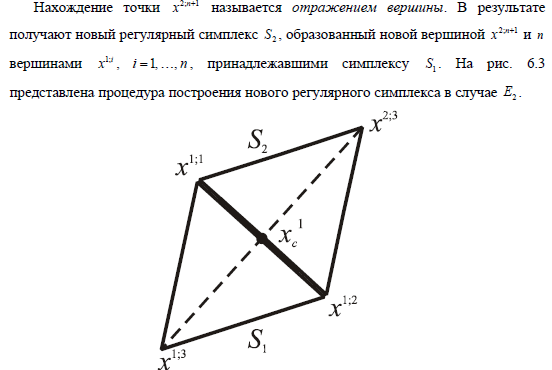
6.3. Описать алгоритм отражения вершины в методе правильного симплекса.

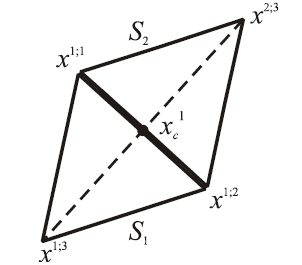
6.4. Зачем необходима и в чем заключается редукция правильного симплекса?

Редукция – уменьшение длина ребра l симплекса S_k.

6.5. Сформулировать теоретическое обоснование минимизации целевой функции методом правильного симплекса.

Твой вопрос? Не повезло 

6.6. В задачах минимизации с какими целевыми функциями метод правильного симплекса не может обеспечить высокой точности?

Симплексные процедуры безусловной минимизации, в которых используются регулярные симплексы, эффективны лишь в тех случаях, когда топография поверхностей уровня целевой функции достаточно проста. В противном случае эффективность применения таких процедур значительно снижается. В частности, это характерно для функций, скорость убывания которых по одному или нескольким направлениям значительно больше, чем по остальным. В таком случае говорят, что график функции имеет овражную структуру.

Примером функции, график которой обладает овражной структурой, является функция Розенброка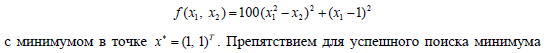

f(x) является в этом случае форма симплекса: регулярный симплекс нельзя изменить так, чтобы он "вытянулся" вдоль "оврага", а это не позволяет продолжить поиск минимума. В этих случаях естественной выглядит идея деформирования симплекса в процессе поиска, т.е. изменения его формы и размера.

6.7. Сформулировать особенности минимизации целевой функции методом Нелдера-Мида по сравнению с ее минимизацией методом правильного симплекса.

6.8. Назвать класс целевых функций, при минимизации которых метод Нелдера-Мида имеет преимущество перед минимизацией по регулярному симплексу.

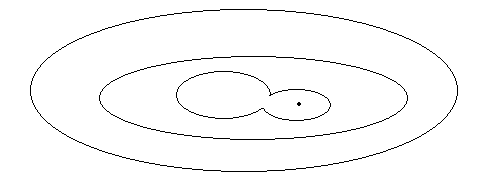
Этот метод хорош при минимизации функций, которые имеют искривленный овражный характер.

6.9. Сформулировать теоретическое обоснование минимизации целевой функции методом Нелдера-Мида.

Твой вопрос? Не повезло 

6.10. Назвать класс унимодальных целевых функций, для которых эффективна минимизация методом циклического покоординатного спуска.

Метод эффективен в случае, если минимизируемая функция является сепарабельной, т.е. представляет собой сумму функций, каждая из которых зависит лишь от одной координаты

В этом случае решение задачи минимизации можно получить за один шаг поиска. Действительно, т.к. то достаточно на первом шаге поиска последовательно решить n задач одномерной минимизации функции что позволит найти все n координат x*_j искомой точки x*. Для функция общего вида эффективность поиска минимума методом циклического покоординатного спуска может быть значительно ниже.

6.11. Как можно дополнительно повысить эффективность поиска точки минимума целевой функции, которая ищется методом циклического покоординатного спуска?

Эффективность решения задачи методом циклического покоординатного спуска можно повысить. Для этого следует дополнить его алгоритм периодически повторяющимся поиском точки минимума в направлении pⁱ=xⁱ-x^i-2 из точек xⁱ.