Глава 3

3.1. Пусть − выпуклая дифференцируемая функция и . Можно ли указать погрешности определения точки минимума x* и минимального значения f* по формулам ∗ ∗? Ответ пояснить рисунком.

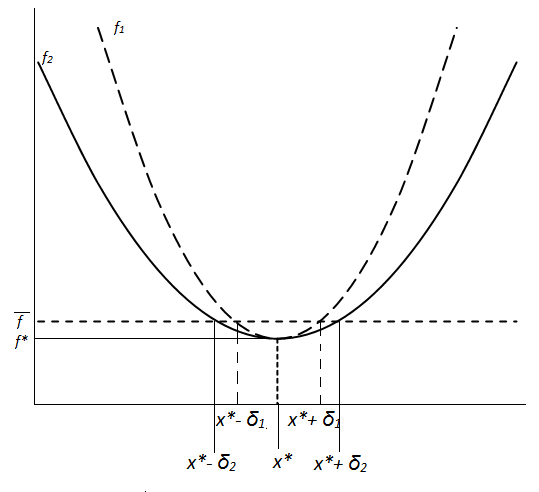
Ответ: Нет, нельзя. Возьмем для примера функцию x² и 2x². f* и x* - точка минимума. При погрешности в ε получаем разброс возможных значений функции (от до f*). Найденная точка по оси ОУ будет лежать в интервале , следовательно погрешность одинакова, однако погрешности по ОХ различны: δ₁<δ₂.

3.2. Является ли условие достаточным для того, чтобы число x было точкой минимума унимодальной, но не выпуклой функции ? Ответ сопроводить примером.

Нет. Пример: функция y=x³. В точке (0,0) производная равна 0, однако она не является точкой минимума.

3.3. Указать класс функций, для которых точное определение точки минимума гарантировано в результате всего одной итерации метода Ньютона.

Квадратичная фукнция

3.4. Сформулировать достаточные условия сходимости метода Ньютона

3.5. Сформулировать достаточные условия монотонной сходимости метода Ньютона. Всегда ли в этом случае скорость сходимости будет квадратичной?

Монотонная сходимость {x_k} к x^*

Достаточное условие монотонной сходимости метода Ньютона

Нет

3.6 Для каких выпуклых дважды дифференцируемых функций метод золотого сечения приводит к цели за меньшее количество итераций, чем метод Ньютона?

3.8. Сформулировать оценку погрешности определения минимума многомодальной функции методом перебора.

3.9. Увеличение используемого значения константы Липшица L при реализации метода ломаных приводит к замедлению сходимости метода. Объяснить этот факт с помощью геометрической иллюстрации

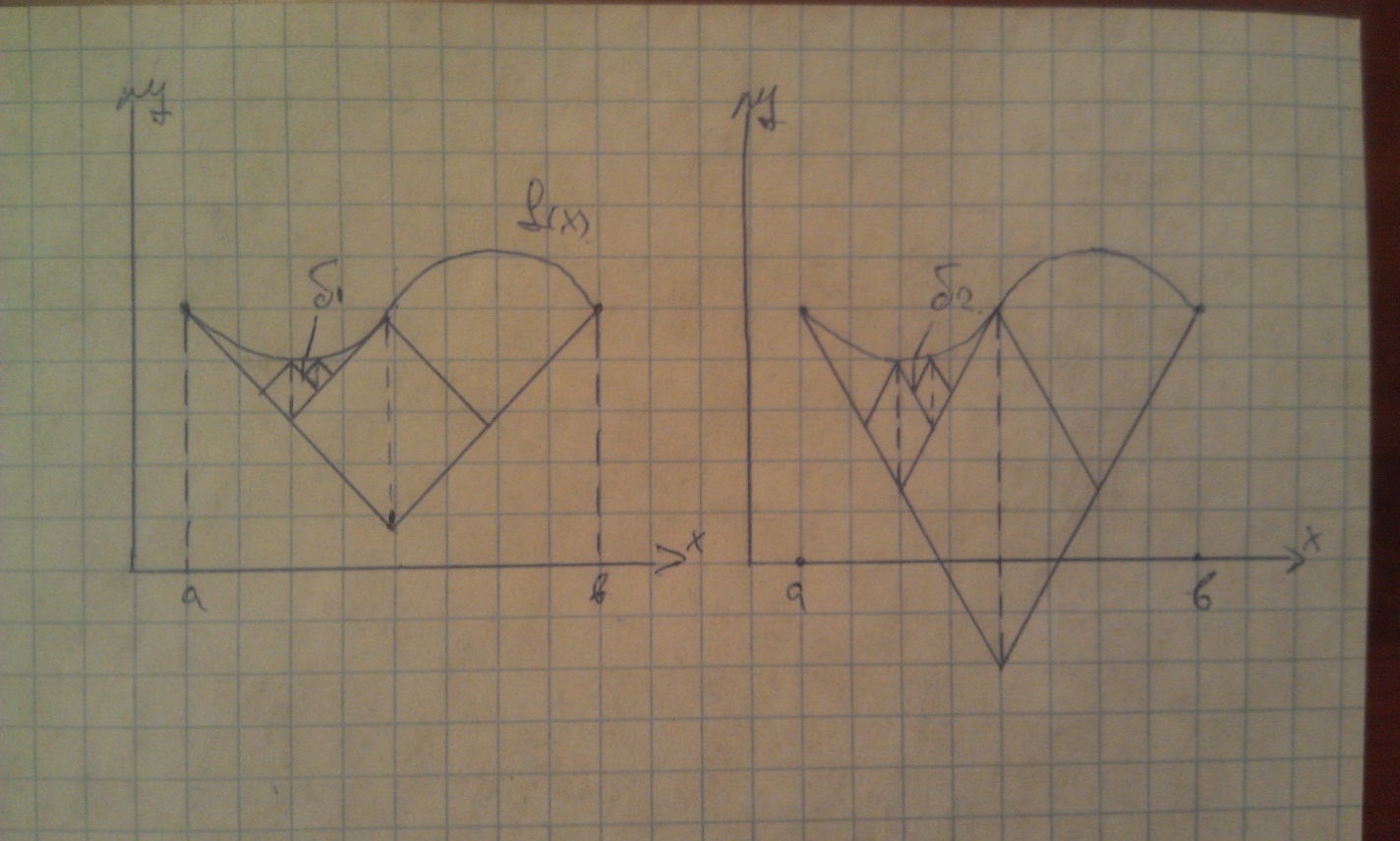
L₁<L₂

δ₁<δ₂

3.10. Показать с помощью рисунка, что если в методе ломаных используется ошибочно заниженное значение константы Липшица L, то задача минимизации может быть решена неверно.

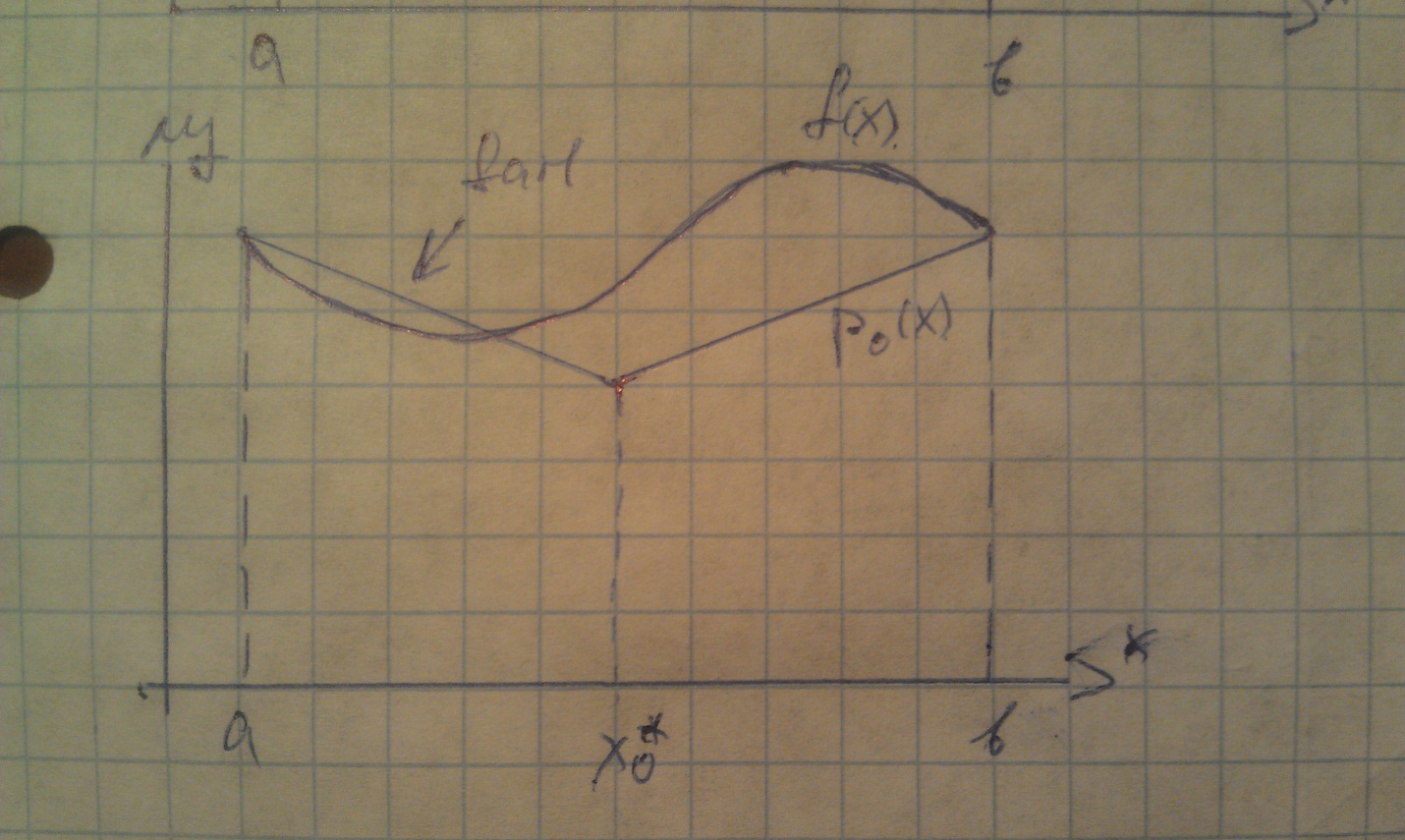
Глава 4

4.1.Что такое градиент и антиградиент функции многих переменных и каков их геометрический смысл?

Определение. Градиентом ∇f(x) непрерывно дифференцируемой функции f(x) в точке x называется вектор-столбец, элементами которого являются частные производные первого порядка, вычисленные в данной точке

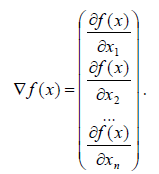
Градиент функции направлен по нормали к поверхности уровня, т.е. перпендикулярно к касательной плоскости, проведенной в точке x, в сторону наибольшего возрастания функции в данной точке.

Антиградиент равен по модулю вектору градиента, но противоположен по направлению. Он указывает в сторону наибольшего убывания функции в данной точке.

4.2. Что такое матрица Гессе функции многих переменных?

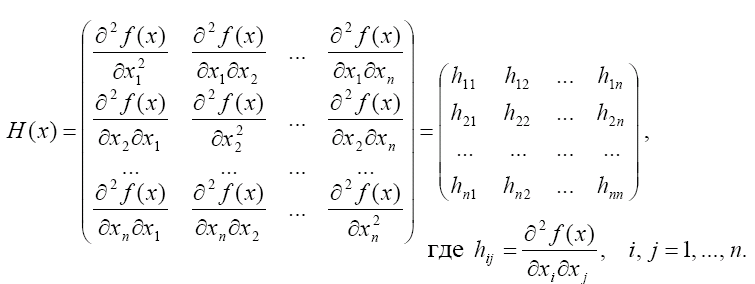
4.3. Записать приращение функции в точке x через градиент и матрицу Гессе.

С помощью градиента и матрицы Гессе, используя разложение в ряд Тейлора, приращение функции может быть записано в форме

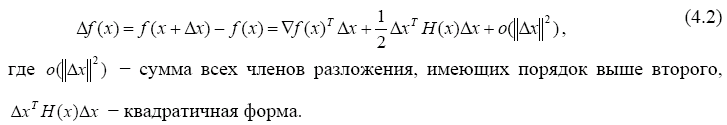
4.4. Вычислить и нарисовать градиенты, а также вычислить матрицу Гессе функции градиент: =(2*х_1, -2*х₂₎

Вычисленный: =(2, 2) Матрица Гессе:

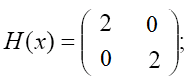
4.5. Классифицировать квадратичные формы и соответствующие им матрицы Гессе

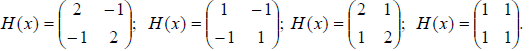
А) 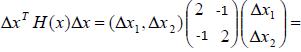(2∆x1-∆x2)∆x1+∆x2(-∆x1+2∆x2)

b) (∆x1-∆x2)∆x1+∆x2(-∆x2+∆x1)

c) (2∆x1+∆x2)∆x1+∆x2(∆x1+2∆x2)

d) (∆x1+∆x2)∆x1+∆x2(∆x1+∆x2)

4.6. Почему в этой главе и далее в книге рассматриваются, в основном, выпуклые функции?

Иначе, решение задач сводилось бы к простому сравнению значений функции на концах отрезка.

4.7. Дать определение выпуклого множества. Сформулировать его геометрический смысл.

Образно говоря, выпуклыми являются множества, которые не содержат "вмятин", "дырок", и состоят из одного "куска". Примерами выпуклых множеств являются само пространство E_n, отрезок, прямая, шар.

4.8. Дать определение выпуклой функции. Сформулировать геометрическую интерпретацию этого свойства, свойство матрицы Гессе выпуклой функции.

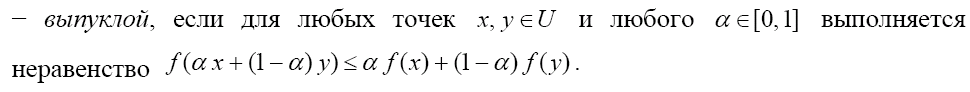
Графическая интерпретация:

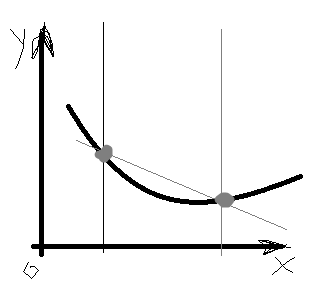
4.9. Дать определение строго выпуклой функции. Сформулировать геометрическую интерпретацию этого свойства, свойство матрицы Гессе строго выпуклой функции.

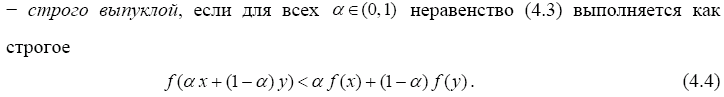
Функцию называют строго выпуклой, если ее график целиком лежит ниже отрезка, соединяющего две ее произвольные, но не совпадающие точки.

Если функция строго выпуклая, то она одновременно выпуклая.

4.10. Дать определение сильно выпуклой функции. Сформулировать свойство матрицы Гессе сильно выпуклой функции.

4.11. Исследовать на выпуклость функции:

4.12. Какие свойства выпуклых функций Вы знаете?

4.13. Сформулировать необходимое условие первого порядка для безусловного экстремума функции многих переменных.

4.14. Сформулировать необходимое условие второго порядка для безусловного

экстремума функции многих переменных.

4.15. Сформулировать достаточное условие безусловного экстремума функции многих переменных.

4.16. Что такое угловые миноры и главные миноры квадратной матрицы?

4.17. Сформулировать критерий Сильвестра проверки достаточных условий безусловного экстремума функции многих переменных.

4.18. Сформулировать критерий проверки необходимых условий экстремума второго порядка функции многих переменных.

4.19. Сформулировать второй способ проверки условий экстремума функции многих переменных (через собственные значения матрицы Гессе).

Второй способ проверки условий экстремума связан с анализом собственных значений матрицы Гессе и применим только в случае, если эти значения удается вычислить.

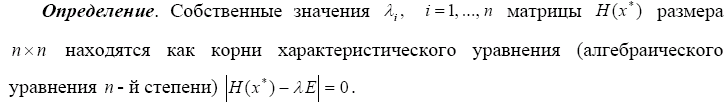
Необходимо отметить, что собственные значения вещественной симметрической матрицы H(x^*) вещественны.

Если собственные значения матрицы Гессе вычислены, то дальнейшая проверка условий экстремума не составляет затруднений.

4.20. Сформулировать необходимые и достаточные условия безусловного экстремума функции одной переменной.