Глава 1

1.1.Какая функция называется целевой?

Многие задачи оптимизации сводятся к отысканию наименьшего или наибольшего значения некоторой функции, которую принято называть целевой функцией. Такая постановка задачи будет обычной при дальнейшем изложении. В этом случае методы исследования существенно зависят от свойств целевой функции и той информации о ней, которая может считаться доступной до решения задачи и в процессе решения.

1.2.Дать определение локального и глобального минимумов функции.

1.3. Что такое точная нижняя грань функции на множестве?

1.4. Как соотносятся точная нижняя грань и минимум функции на множестве?

Если . Таким образом, точная нижняя грань обобщает понятие минимума функции на случай

1.5. Какая функция называется унимодальной на отрезке [a,b]?

1.6. Сформулировать свойства унимодальных функций.

Из определения вытекают следующие свойства унимодальных функций.

1. Любая из точек локального минимума унимодальной функции является и точкой ее глобального минимума на отрезке [a,b].

2. Функция, унимодальная на отрезке [a,b], унимодальна и на любом меньшем отрезке

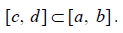
3. Пусть f(x) унимодальна на [a,b] и Тогда

1.7. Какая функция называется выпуклой на отрезке [a,b]?

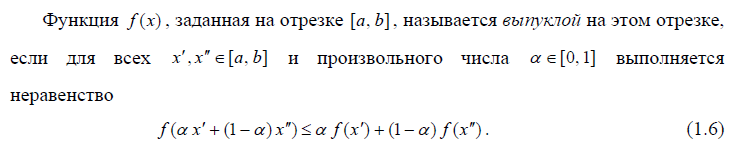
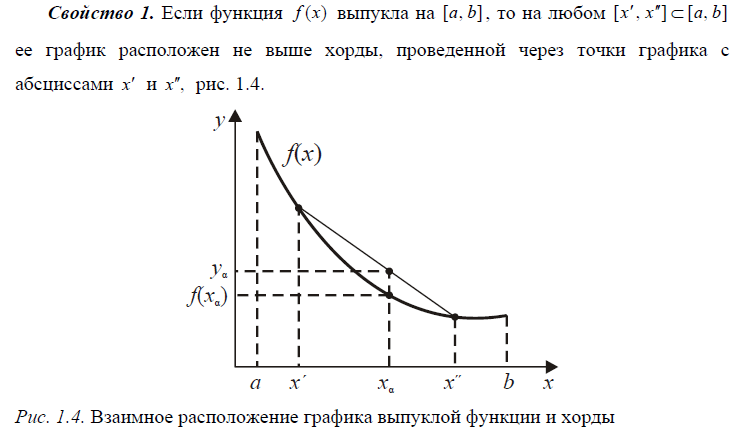
1.8. Каков геометрический смысл выпуклости функции?

1.9. Сформулировать два необходимых и достаточных дифференциальных условий выпуклости функций.

1.10. Сформулировать условие Липшица для функции f(x) на отрезке [a,b]

1.11. Всякая ли унимодальная на отрезке [a,b] функция f(x) удовлетворяет на нем условию Липшица?

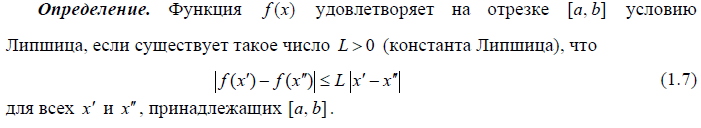
1.12. Всякая ли функция f(x), удовлетворяющая условию Липшица на отрезке [a,b], унимодальна на нем?

1.13. Сформулировать свойства функций, удовл. на отрезке [a,b] условию Липшица.

1.14. В чем заключается классический метод минимизации функций, 1.15 Для каких целей разработан классический метод минимизации функций, 1.16 Какова практическая ограниченность применимости этого метода?

Глава 2

2.1.Пусть f(x) – дифференцируемая унимодальная на отрезке [a,b] функция, причем

. Оценить точность ∆(N) при определении минимального значения f’ методом перебора в результате N вычислений f(x).

|x* - x_n| < E(n)

f ` (x_n)= - f(x)

f ` (x_n)= (f(x) – f(x_n))/∆

f(x_n) ≤ ∆M

∆N= M(b-a)/N-1

2.2. Может ли оценка ε(N)= для точности определения х* методом перебора для функций, не являющихся унимодальными. Ответ пояснить рисунком.

Может, так как большой шаг.

2.3. Повысится ли эффективность метода поразрядного поиска, если шаг поиска ∆ последовательно уменьшать не в четыре, а в какое-либо другое количество раз?

Однозначного ответа нет, но можно рассмотреть предельные случаи:

- если уменьшать отрезки в 2 раза, а не в 4, то поиск будет часто менять свое направление.

- если уменьшать отрезки в большее число раз (100, 1000…), то метод не будет эффективен, так как это будет почти метод перебора.

2.4. Может ли применение методов исключения отрезков привести к неверному определению х*, если функция f(X) не унимодальная. Ответ пояснить рисунком.

Пояснение: рассмотрим на графике две точки: х1 и х2, значения функции в точке х2 меньше, чем в точке х1, следовательно, согласно методу исключения отрезков, мы исключаем отрезок [a,x1] и теперь рассматриваем только [x1, b]. Таким образом, реальный минимум функции остается в исключенном отрезке и минимум функции определяется неправильно.