
- •Вопрос 8 Сила тяжести и ускорение свободного падения
- •Трение покоя
- •Виды кинематического трения
- •Вопрос 9 Механическая работа
- •Мощность
- •Вопрос 10
- •Кинетическая энергия
- •5.2. Потенциальное поле сил
- •Консервативные силы (физика)
- •Связь между потенциальной энергией и силой
- •. Упругие и неупругие соударения
- •Вопрос 17
- •8) Вращение твердого тела вокруг неподвижной оси. Скорости и ускорения точек тела (векторные и скалярные выражения).
- •3.1. Основные положения мкт
- •Основное уравнение мкт газов. Температура
- •Степеней свободы число
- •Распределение Максвелла
- •Распределение Максвелла
- •Границы применимости
- •[Править] Условия классического рассмотрения
- •5.5. Экспериментальная проверка распределения Максвелла
- •Опыт Ламмерта
- •Суть эксперимента
- •Барометрическая формула
- •Первое начало термодинамики
- •Формулировка
- •Частные случаи
- •Формулировка
- •Другие определения
- •Теплоёмкость для различных состояний вещества
- •Теория теплоёмкости
- •Основное уравнение термодинамики для адиабатического процесса
- •Уравнение Пуассона
- •Показатель адиабаты
- •] Формулировки
- •Ограничения
- •Второе начало термодинамики и «тепловая смерть Вселенной»
- •Энтропия и критика эволюции
- •Неравенство Клаузиуса
- •Выведение Частный случай: два тепловых резервуара
- •Общий случай: много тепловых резервуаров
- •Cледствия
- •Критические параметры
- •Приведённые параметры
- •Перенос энергии
- •Сила вязкого трения
- •Вязкость газов
- •Дифференциальное уравнение движения физического маятника
- •Центр качания физического маятника
- •[Править] Период малых колебаний физического маятника
- •Уравнение колебаний маятника
- •Решения уравнения движения Гармонические колебания
- •Нелинейный маятник
- •Движение по сепаратрисе
- •Затухающие колебания пружинного маятника
- •Математическое выражение для кривой Лиссажу
- •Применение в технике — сравнение частот
- •Силы инерции при произвольном ускоренном движении системы отсчета
- •Формулировка
- •Получение
- •Количественное рассмотрени
- •Сила инерции в неинерциальной системе отсчёта
. Упругие и неупругие соударения
Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.
В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.
Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.
При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).
Примером
абсолютно неупругого удара может
служить попадание пули (или снаряда) в
баллистический
маятник. Маятник
представляет собой ящик с песком массой
M,
подвешенный на веревках (рис. 1.21.1).
Пуля массой m,
летящая горизонтально со скоростью
![]() попадает
в ящик и застревает в нем. По отклонению
маятника можно определить скорость
пули.
попадает
в ящик и застревает в нем. По отклонению
маятника можно определить скорость
пули.
Обозначим
скорость ящика с застрявшей в нем пулей
через
![]() Тогда
по закону сохранения импульса
Тогда
по закону сохранения импульса
|
При застревании пули в песке произошла потеря механической энергии:
|
Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:
|
Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.
При
m << M  почти вся кинетическая энергия пули
переходит во внутреннюю энергию. При
m = M
почти вся кинетическая энергия пули
переходит во внутреннюю энергию. При
m = M  – во внутреннюю энергию переходит
половина
– во внутреннюю энергию переходит
половина
первоначальной
кинетической энергии. Наконец, при
неупругом соударении движущегося тела
большой массы с неподвижным телом малой
массы (m >> М)
отношение

Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:
|
где h – максимальная высота подъема маятника. Из этих соотношений следует:
|
Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.
Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.
При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.
Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).
Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.
|
Абсолютно упругий центральный удар шаров |
В общем случае массы m1 и m2 соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии
|
Здесь υ1 – скорость первого шара до столкновения, скорость второго шара υ2 = 0, u1 и u2 – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:
m1υ1 = m1u1 + m2u2. |
Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u1 и u2 шаров после столкновения:
|
ВОПРОС 16 |
|
|
|
Механическая система будет находиться в равновесии, если на неё не будет действовать сила. Это условие необходимое, но не достаточное, так как система может при этом находиться в равномерном и прямолинейном движении. Рассмотрим пример, изображенный на рис. 5.7.
Здесь, даже при отсутствии силы, положение в точке x2 нельзя назвать устойчивым равновесием. По определению, Fx = 0 – условие равновесия системы. Учитывая формулы
(5.3.7)
имеем
Именно так находят положение точек экстремума. Возвращаясь к рисунку 5.7, заметим, что при x = x1 и x = x2. Точка x = x1 соответствует состоянию устойчивого равновесия (потенциальный барьер), тогда как точка x = x2 - состоянию неустойчивого равновесия (потенциальная яма). Таким образом, достаточным условием равновесия является равенство минимуму значения U (это справедливо не только для механической системы, но, например, и для атома). |





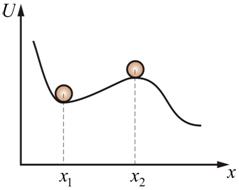 Рис.
5.7
Рис.
5.7