
- •Вопрос 8 Сила тяжести и ускорение свободного падения
- •Трение покоя
- •Виды кинематического трения
- •Вопрос 9 Механическая работа
- •Мощность
- •Вопрос 10
- •Кинетическая энергия
- •5.2. Потенциальное поле сил
- •Консервативные силы (физика)
- •Связь между потенциальной энергией и силой
- •. Упругие и неупругие соударения
- •Вопрос 17
- •8) Вращение твердого тела вокруг неподвижной оси. Скорости и ускорения точек тела (векторные и скалярные выражения).
- •3.1. Основные положения мкт
- •Основное уравнение мкт газов. Температура
- •Степеней свободы число
- •Распределение Максвелла
- •Распределение Максвелла
- •Границы применимости
- •[Править] Условия классического рассмотрения
- •5.5. Экспериментальная проверка распределения Максвелла
- •Опыт Ламмерта
- •Суть эксперимента
- •Барометрическая формула
- •Первое начало термодинамики
- •Формулировка
- •Частные случаи
- •Формулировка
- •Другие определения
- •Теплоёмкость для различных состояний вещества
- •Теория теплоёмкости
- •Основное уравнение термодинамики для адиабатического процесса
- •Уравнение Пуассона
- •Показатель адиабаты
- •] Формулировки
- •Ограничения
- •Второе начало термодинамики и «тепловая смерть Вселенной»
- •Энтропия и критика эволюции
- •Неравенство Клаузиуса
- •Выведение Частный случай: два тепловых резервуара
- •Общий случай: много тепловых резервуаров
- •Cледствия
- •Критические параметры
- •Приведённые параметры
- •Перенос энергии
- •Сила вязкого трения
- •Вязкость газов
- •Дифференциальное уравнение движения физического маятника
- •Центр качания физического маятника
- •[Править] Период малых колебаний физического маятника
- •Уравнение колебаний маятника
- •Решения уравнения движения Гармонические колебания
- •Нелинейный маятник
- •Движение по сепаратрисе
- •Затухающие колебания пружинного маятника
- •Математическое выражение для кривой Лиссажу
- •Применение в технике — сравнение частот
- •Силы инерции при произвольном ускоренном движении системы отсчета
- •Формулировка
- •Получение
- •Количественное рассмотрени
- •Сила инерции в неинерциальной системе отсчёта
Основное уравнение термодинамики для адиабатического процесса
Для адиабатического процесса первое начало термодинамики в силу отсутствия теплообмена (ΔQ = 0) системы со средой имеет вид
![]()
где:
 —
изменение внутренней
энергии тела,
—
изменение внутренней
энергии тела,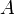 —
работа, совершаемая
системой
—
работа, совершаемая
системой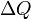 —
теплота, полученная
системой
—
теплота, полученная
системой
Основное уравнение термодинамики применительно к адиабатическому процессу записывается в дифференциалах как
![]() ,
,
где
![]() —
дифференциальное выражение для работы,
ai
— внешние параметры, Ai
— соответствующие им внутренние
параметры. В частном случае, когда
работа совершается через изменение
объёма
—
дифференциальное выражение для работы,
ai
— внешние параметры, Ai
— соответствующие им внутренние
параметры. В частном случае, когда
работа совершается через изменение
объёма
![]() ,
где p
— давление.
,
где p
— давление.
Энтропия системы в адиабатическом процессе не меняется:
![]() .
.
Уравнение Пуассона
Для идеальных газов адиабата имеет простейший вид и определяется уравнением:
![]()
где:
 —
давление
газа,
—
давление
газа, —
его объём,
—
его объём, —
показатель
адиабаты,
—
показатель
адиабаты, и
и
 —
теплоёмкости
газа соответственно при постоянном
давлении и постоянном объёме.
—
теплоёмкости
газа соответственно при постоянном
давлении и постоянном объёме.
Показатель адиабаты
Для
нерелятивистского невырожденного
одноатомного идеального газа
![]() ,
для двухатомного
,
для двухатомного
![]() ,
для трёхатомного
,
для трёхатомного
![]() ,
для газов состоящих из более сложных
молекул, показатель адиабаты,
,
для газов состоящих из более сложных
молекул, показатель адиабаты,
![]() определяется
числом степеней
свободы
конкретной молекулы.
определяется
числом степеней
свободы
конкретной молекулы.
При
адиабатическом процессе показатель
адиабаты равен
![]() ,
где R — универсальная
газовая постоянная.
,
где R — универсальная
газовая постоянная.
С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду:
![]() ,
где T
— абсолютная
температура
газа.
,
где T
— абсолютная
температура
газа.
Или к виду:
![]()
Поскольку всегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (т.е. при уменьшении V) газ нагревается (T возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов.
Вариант 46
Круговой
процесс — процесс, при котором газ,
пройдя через ряд состояний, возвращается
в исходное.
Если круговой процесс
на диаграмме P-V протекает по часовой
стрелке, то часть тепловой энергии,
полученной от нагревателя, превращается
в работу. Так работает тепловая
машина.
Если круговой процесс на
диаграмме P-V протекает против часовой
стрелки, то тепловая энергия передается
от холодильника (тела с меньшей
температурой) к нагревателю (телу с
большей температурой) за счет работы
внешней силы. Так работает холодильная
машина.
 Коэффициент
полезного действия тепловой
машины равен отношению работы
Коэффициент
полезного действия тепловой
машины равен отношению работы
![]() за
цикл к полученной от нагревателя
тепловой энергии
за
цикл к полученной от нагревателя
тепловой энергии
![]() :
:
![]() .
Холодильный
коэффициент холодильной машины
равен отношению тепловой энергии
.
Холодильный
коэффициент холодильной машины
равен отношению тепловой энергии
![]() ,
отобранной от холодильника за цикл, к
затраченной работе
:
,
отобранной от холодильника за цикл, к
затраченной работе
:
![]() .
.
Цикл Карно — круговой процесс, состоящий из двух изотерм и двух адиабат.
1
– 2 — изотермическое сжатие при
температуре
![]() ,
,
![]() .
2
– 3 — адиабатическое расширение от
температуры
до
.
2
– 3 — адиабатическое расширение от
температуры
до
![]() ,
,
![]() .
3
– 4 — изотермическое сжатие при
температуре
,
.
3
– 4 — изотермическое сжатие при
температуре
,
![]() 4
– 1 — адиабатическое сжатие от температуры
до
,
4
– 1 — адиабатическое сжатие от температуры
до
,
![]() .
Согласно
уравнению Пуассона:
.
Согласно
уравнению Пуассона:
 .
Коэффициент
полезного действия (кпд) цикла Карно —
отношение суммарной работы за цикл к
полученному теплу:
.
Коэффициент
полезного действия (кпд) цикла Карно —
отношение суммарной работы за цикл к
полученному теплу:
 ,
,
 .
Таким
образом, кпд цикла Карно всегда меньше
единицы (100%) и зависит только от
соотношения температур холодильника
и нагревателя:
.
Таким
образом, кпд цикла Карно всегда меньше
единицы (100%) и зависит только от
соотношения температур холодильника
и нагревателя:
![]() .
.
Вариант 47
|
Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.
Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая невозможность перехода всей внутренней энергии системы в полезную работу.
Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.
|
|
