Тема 6. Денежные потоки и их использование в инвестиционном анализе

При изучении денежных потоков используют понятия будущей и настоящей стоимости, являющиеся аналогами операций наращивания сложных процентов и дисконтирования:

FV=PV(1+i)ⁿ, PV=FV/(1+(1+i)ⁿ

где i - величина доходности инвестиций;

n - рассматриваемый отрезок времени;

FV - будущая стоимость (future value)

PV - настоящая, текущая, современная стоимость (present value).

Поток платежей, все члены которого - положительные величины, а временные интервалы между платежами одинаковы, называют финансовой рентой или просто рентой, а иногда аннуитетом. Строго говоря, последнее наименование предполагаем только ежегодные платежи, однако на практике оно применяется более широко - для обозначения любого вида регулярной последовательности платежей.

Сам же ежегодный платеж также называют аннуитетом или рентным платежом.

В начале рассматривается приток (отток) денежных средств по схеме постнумерандо, имеющий вид:

I₀ a₁ a₂ a₃ a_n

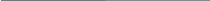
0 1 2 3 n

Здесь I₀ - инвестиция;

a₁, a₂, ..., a_n - потоки платежей (приход или расход) в конце каждого года при i% годовых;

n - рассматриваемый период времени.

Текущая стоимость ряда вкладов постнумерандо будет

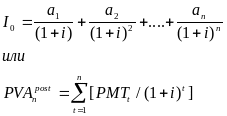
Здесь - современная стоимость аннуитета постнумерандо за n лет;

- разовый платеж (payment) в году t.

Рассмотрим случай, когда

а₁= а₂=... а_n=РМТ=а

Тогда ,

где - коэффициент приведения или коэффициент дисконтирования вкладов.

То же самое в новой символике можно записать

- текущая (современная) стоимость аннуитета стоимостью в 1 руб. В конце каждого из n периодов при ставке доходности по уровне i.

Для рассматриваемого потока будущая стоимость аннуитета рассчитывается по формуле

или при равенстве ежегодных платежей

где =[(1+i)-1]/i - будущая стоимость аннуитета в 1 руб в конце каждого периода получения доходов на протяжении n периодов и при ставке процентного дохода на уровне i.

Далее переходят к рассмотрению потока пренумерандо. Схема пренумерандо имеет вид:

I₀

a₁ a₂ a₃ a_n

0 1 2 n-1 n

где а₁, а₂, ..., а_n - потоки платежей (приход или расход) в начале каждого года при i% годовых.

Текущая стоимость ряда вкладов пренумирандо будет

Рассмотрим случай, когда

а₁=а₂= ...= а_n=а=РМТ

Тогда

) или

)

Примером альтернативного аннуитету вложения является перпетуитет (англ. perpetuity - вечность) - банковский текущий (сберегающий) счет, процентный доход начисления. В этом случае возникает ситуация, когда основная сумма как бы «зарабатывает» деньги на предстоящий год, а срок жизни инвестиции неограничен.

В этом случае годовой доход определяется по формуле: РМТ=PVi,

где PV - основная сумма сбережений на банковском счете,

i - процентная ставка дохода, выплачиваемая банком по счетам данного типа.

Последнее соотношение приводит к пониманию логики инвестиционного анализа: если простое помещение денежной суммы PV на сберегательный счет обеспечивает ежегодный доход в сумме РМТ, то нет смысла выделять денежную сумму более величины PV на реализацию инвестиционного проекта, который может обеспечить получение в начале каждого очередного года дохода на уровне РМТ.

Особый случай перпетуитета - инвестиция с неограниченным сроком жизни, но с постоянно возрастающими величинами годового дохода.

Если такой рост происходит с темпом, равным g, а РМТ₁ означает ожидаемую величину денежных поступлений в конце первого года, тогда текущая (современная) стоимость такой «вечной» инвестиции будет

PV=PMT₁/(i-g)

Эту модель называют формулой Гордона.

Перейдем к рассмотрению некоторых характеристик денежных потоков, в частности, среднего срока потока платежей. Под средним сроком потоков платежей (например, получения доходов на вложенные капиталы a₁, a₂, ..., a_n в момент t₁, t₂, . . . ,t_n) понимают момент, в который дисконтированная сумма всех платежей равняется сумме дисконтированных стоимостей всех платежей. По определению:

(*)

Используя биномиальное разложение, получим:

Отбрасывая член, содержащий i², и упрощая соотношение (*), получаем:

a₁(1-t₁i)+ a₂(1-t₂i)+. . .+ a_n(1-t_ni)=( a₁+ a₂+. . . + a_n)(1-t_ai)

или

a₁t₁i+ a₂t₂i+ . . .+ a_nt_ni = ( a₁+ a₂+. . . + a_n)t_ai

Отсюда t_a= (a₁t₁+ a₂t₂+ . . .+ a_nt_n)/( a₁+ a₂+. . . + a_n)

Далее при изложении материала будет использоваться понятие годового чистого денежного потока R, который по определению равен:

R=(РП-С-А)(1-Н_n)+A, где

РП - выручка от проекта;

С - затраты (кроме амортизационных отчислений);

А - амортизационные отчисления;

Н_n - ставка налогообложения прибыли.

Денежные потоки используются при расчете эффективности инвестиционных проектов. Прежде чем переходить к рассмотрению этого вопроса, необходимо напомнить слушателям известное им из курса «Экономика фирмы» характеристики эффективности инвестиционных проектов. К ним относятся: абсолютная эффективность; срок окупаемости дополнительных капитальных вложений; коэффициент сравнительной эффективности дополнительных капитальных вложений; приведенные затраты.

Проект принимается, если его абсолютная или сравнительная эффективность выше нормативной, а срок окупаемости ниже нормативного. Из рассматриваемых вариантов выбирается проект с наименьшими приведенными затратами. Здесь следует разъяснить рыночный смысл приведенных затрат как минимальной «цены производства». В рыночной экономике формула расчета приведенных затрат П3 имеет вид:

П3=С+iК,

где С - себестоимость продукции после реализации проекта;

К - объем капитальных вложений;

i - ставка ссудного процента.

Добавленная к себестоимости величина iК представляет собой либо упущенную выгоду (если капитальные вложения осуществляются за счет собственных ресурсов), либо - проценты за кредит (если для реализации инвестиционного проекта взят кредит, равный объему капитальных вложений).

Затем переходят к рассмотрению характеристик эффективности инвестиционных проектов, используемых в рыночной экономике. Это - внутренний уровень доходности, чистая современная стоимость проекта период окупаемости инвестиций и их рентабельность.

Внутренний уровень доходности (ВУД) определяется как ставка i, при которой вложенные инвестиции I₀ были бы равны сумме дисконтированных чистых потоков R_t от эксплуатации проекта в каждом году t:

В международной символике ВУД обозначается аббревиатурой IIR - Internal Rate of Return.

Чистая современная (текущая) стоимость ЧСС проекта или международной символике NPV - Net Present Value представляет собой разность между суммой дисконтированных чистых денежных потоков от реализации проекта и вложенной инвестицией:

сопоставляя это выражение с приведенным выше, убеждаемся, что внутренний уровень доходности - такая процентная ставка, при которой разность между суммой дисконтированных доходов и начальной инвестицией равна нулю.

Если инвестиции рассредоточены во времени, то формула для расчета NPV имеет вид

Период окупаемости инвестиций рассчитывается по формуле:

,

где РР - период окупаемости, лет (payback period);

I₀ - первоначальная инвестиция (investment);

- среднегодовой, чистый денежный поток.

И, наконец, рентабельность инвестиций оценивают по формуле:

Здесь PI - рентабельность инвестиций, доли (profitability index).

Проект принимается, если NPV0 или если IRR или PI больше заданных барьерных коэффициентов.

Затем переходят к более подробному рассмотрению характеристик, используемых для оценки эффективности инвестиционных проектов, в частности, периода окупаемости инвестиционного проекта. Одно из определений этого периода было дано выше: период окупаемости инвестиций рассчитывается как частное от деления инвестиции на среднегодовой чистый денежный поток от реализации проекта.

В соответствии со вторым определением за момент окупаемости проекта принимается момент времени, в который накопленная сумма денежных поступлений от реализации проекта начинает превосходить величину инвестиции.

Пусть, например, I₀=600 млн. руб., а R₁=100; R₂=150; R₃=200; R₄=300; R₅=350 млн. руб. - соответствующие чистые денежные потоки. Убеждаемся в том, что млн. руб. превышаем I₀. В то же время млн. руб.I₀. Это означает, что срок окупаемости проекта не превышает четырех лет. Для нахождения точного значения периода окупаемости составляют балансовое соотношение:

100+150+300х=600, где х - отрезок времени (в долях), приходящийся за четвертый год эксплуатации проекта, в который завершается его окупаемость.

Находим, что Х=0,5 года, а если период окупаемости проекта равен РР=3,5 года.

Можно осуществлять расчет периода окупаемости с учетом операции дисконтирования. Полезно убедиться в том, что использование этой процедуры приводит к удлинению периода окупаемости.

Кроме того полезно убедиться, что период окупаемости имеет прямую связь с используемым значением ставки дисконтирования.

Покажем, например, что проект с пятилетним сроком окупаемости и десятилетним сроком жизни предполагает значение ставки дисконтирования на уровне15%. Действительно, пятилетний период окупаемости означает, что ежегодные денежные поступления должны составлять не менее 20% от суммы первоначальных инвестиций, т.е. на каждые 100 руб. инвестиций получаем в год не менее 20 руб. денежных поступлений. Имеем балансовое соотношение:

100=20PVA1_{10 лет, i%}

или

PVA1_{10 лет,i%}=5

По таблицам текущей стоимости аннуитета стоимостью в 1 руб. находим, что последнее равенство выполняется при i=15%. При этом наиболее близкая к 5 величина PVA1_{10 лет, i%}

равна 5,019.

Величина, обратная сроку окупаемости, называется коэффициентом эффективности инвестиций Е. в то же время коэффициент эффективности равен отношению среднегодового чистого денежного потока к начальным капитальным вложениям. Таким образом:

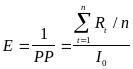
Можно показать, что коэффициент эффективности проекта при длительных сроках его эксплуатации приближается к внутреннему уровню доходности.

Рассмотрим денежный поток постнумерандо для случая равных чистых денежных потоков, т.е. для случая когда R₁= R₂=. . . R_n= R_.

Ранее было получено соотношение:

Здесь i - ставки дисконтирования, равная внутреннему уровню доходности проекта.

Отсюда:

Переходя к пределу, имеем

Но

Тогда

Таким образом, величина, обратная среднему сроку окупаемости (коэффициент эффективности капитальных вложений) при длительных сроках эксплуатации проекта приближается к внутреннему уровню доходности.

Необходимо уяснить также зависимость чистой современной стоимости от ставки дисконтирования. Действительно:

Отсюда при и при .

Пусть Р₁, Р₂, . . . , Р_n - доходы в моменты t₁, t₂, . . . , t_n, a C₁, C₂, . . . , C_k - расходы в моменты t₁, t₂, . . . , t_k. По определению ВУД:

Используя определение среднего срока потока платежей, можно записать:

(Р₁+ Р₂+. . . + Р_n) =( С₁+ С₂+ . . +С_к)

или

(Р₁+ Р₂+. . . + Р_n)/ ( С₁+ С₂+ . . +С_к)=

Отсюда получаем формулу для расчета ВУД (IIR):

IRR=i=

Во втором случае для расчета ВУД используют соотношение I₀=RPVA1_n,IRR.

Отсюда PVA1_n,IRR=I₀/R

Далее по таблицам современной стоимости аннуитета находят ближайшие к I₀/R величины современной стоимости такие, что

Затем, зная i₁ и i₂ , а также соответствующие величины современных стоимостей, прибегая к линейной интерполяции можно вычислить IIR.

Далее переходят к обсуждению вопросов, связанных с выбором лучшего из двух альтернативных проектов. Основное внимание здесь уделяется использованию критерия NPV.

При анализе двух проектов А и В с одинаковыми сроками жизни рассчитывают NPV_А и NPV_B. Тогда отдают предпочтение проекту А.

Если же зависимость NPV_А=f₁(i) и NPV_В=f₂(i) в некоторой точке F и до этой точки NPV_АNPV_В , а после нее NPV_А NPV_В, причем абсцисса т. F равна i_F, то нежно величину i_F сравнить со значением выбранной барьерной ставки HR (англ. hardle rate) - стандартного уровня желаемой рентабельности вложений. Далее, если i_FHR, то предпочтение отдается проекту А, в противном случае - проекту В. Заметим, что точку F называют точкой Фишера.

Критерий NPV для сравнения проектов можно использовать только при равной продолжительности их жизни. Если сроки жизни проектов различны, то нужно либо приводить их к одинаковой продолжительности, повторив каждый проект соответствующее число раз, либо воспользоваться эквивалентными аннуитетами ЕА (equivalent annuity).

Эквивалентный аннуитет - это уровневый (стандартный) аннуитет, который имеет ту же продолжительность, что и оцениваемый инвестиционный проект PV, что и NPV этого проекта.

В формуле для расчета PV величина PV заменяется на NPV, а PMT заменяется на ЕА и записывается соотношение:

ЕА=NPV/PVA1_n,i

проект, у которого ЕА окажется наибольшим, будет обеспечивать и наибольшую величину NPV всех денежных поступлений.

При решении задач данного типа пользуются эквивалентными годовыми расходами ЕАС (equivalent annual charge), рассчитываемые по формуле для определения эквивалентного аннуитета. Варианту, обеспечивающему минимальные расходы и отдается предпочтение.