Тема 4. Принцип эквивалентности процентных ставок

Эквивалентные процентные ставки - это такие процентные ставки разного вида, применение которых дает одинаковые финансовые результаты.

Эквивалентные ставки необходимо знать в случаях, когда существует возможность выбора условий финансовой операции и требуется инструмент для корректного сравнения этих условий. Пусть речь идет, например, о сопоставлении эффективности различных кредитных предложений, в которых используются различные процентные ставки. Все предложения пересчитываются на один и тот вид ставки процентов. При этом используются формулы для расчета эквивалентных ставок. Условия для получения кредита будут более выгодными в том случае, где соответствующая эффективная ставка, по которой нужно выплачивать проценты, будет ниже.

Далее рассматривается случай, когда все условия финансовых операций совпадают, т.е. первоначальный капитал, временная база, метод расчета (точный или обыкновенный) процентов и период начисления одинаковы. В противном случае применяются те же рассуждения и преобразования, только полученные формулы будут содержать большее количество переменных.

Эквивалентные ставки вычисляются из условия равенства множителей наращения при различных способах вычисления наращенной суммы.

Приведем примеры таких ставок:

эффективная (эквивалентная) годовая ставка простых процентов

i_э=i_Пm,

где i_П - ставка процентов в период их начисления;

эквивалентные ставки простых и сложных процентов при их начислении 1 раз в году

эквивалентные ставки простых и сложных процентов при начислении процентов m раз в году

эквивалентные непрерывные и дискретные ставки сложных процентов

,

отсюда

;

эквивалентная простая годовая ставка ссудного процента и простая годовая учетная ставка:

откуда

эквивалентные сложная годовая ставка процента и сложная годовая учетная ставка:

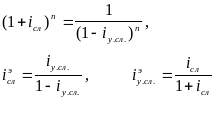
Проанализировав приведенные формулы, можно сделать следующие два вывода:

1. эквивалентность различных процентных ставок не зависит от величины первоначальной суммы S₀, поскольку она предполагалась одинаковой при сопоставлении способов вычисления наращенных сумм.

2. эквивалентность процентных ставок обычно зависит от продолжительности периода начисления, кроме случая когда сопоставляют сложные ставки с одинаковым периодом начисления.

Тема 5. Наращивание процентов в условиях инфляции

Уровень инфляции h показывает на сколько в относительном выражении выросли цены за рассматриваемый период времени: h=S/S, где S - сумма, на которую надо увеличить сумму S для сохранения ее покупательной способности. Индекс же инфляции отвечает на вопрос, во сколько раз увеличились цены за тот же период времени: I_n=(S+S)/S=(1+h). Здесь нужно уметь вычислять годовые уровень h_год и индекс инфляции , если известно месячное значение уровня инфляции:

Для расчета наращенной суммы используются сложные проценты, а для учета влияния инфляции производится дисконтирование по сложной ставке, равной темпу инфляции. Наращенная сумма вычисляется по формуле

Отсюда видно следующее:

если i=h (доходность вложений и уровень инфляции равны), то S=S₀ , т.е. весь доход поглощается инфляцией; если ih (доходность вложений ниже уровня инфляции), то SS₀, т.е. операция приносит убыток; если ih (доходность вложений выше уровня инфляции), то SS₀, т.е. происходит реальный прирост вложений капитала.

Номинальной называют ставку, по которой заключено или заключается кредитное соглашение. Пусть требуется, например, найти номинальную банковскую ставку i_Н - некоторую увеличенную ставку процентов, позволяющую компенсировать влияние инфляции.

Обозначим через i_ч реальную банковскую ставку. Реальная сумма выплат означает, что то количество товаров, которое в момент выплаты можно купить на сумму S₀(1+i_ч) 1 год назад можно было купить на сумму S₀(1+i_Н). С учетом инфляции имеем следующее балансовое соотношение для товарных эквивалентов

_ч)

Понятно, что в данной задаче i_ч равна существующей банковской ставке процентов, таким образом

Решая последнее соотношение относительно номинальной ставки, получаем так называемую формулу И. Фишера:

В то же время можно рассмотреть и обратную задачу.

Известно номинальная банковская ставка i_H (ставки, по которой заключено кредитное соглашение, = i_H ). Известен годовой уровень инфляции h. Требуется определить реальную банковскую ставку.

В этом случае балансовое соотношение для товарных эквивалентов примет вид

отсюда

Возвращаясь к формуле И. Фишера, заметим, что величину , которую нужно прибавить к реальной ставке доходности для компенсации инфляционных потерь, называют инфляционной премией.