3.Синтез кулачкового механизма

3.1 Графическое интегрирование заданного закона движения

Синтез кулачкового механизма начинается с построения диаграммы движения ведомого звена толкателя, исходя из заданной диаграммы

Для построения диаграммы зададимся масштабными коэффициентами:

Далее интегрируем кривую без указания масштабного коэффициента , получаем кривую

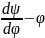
Масштаб обеих кривых связан равенством

(3.1)

где Н – полюсное расстояние.

Аналогичным образом строим кривую , масштаб которой связан масштабом кривой следующим равенством

(3.2)

где Н – полюсное расстояние.

В нашем случае Н = 57,3 мм.

Построив кривую замеряем значение l=10,5мм. Определяем масштабный коэффициент μ_ψ.

из формулы (3.2) определим :

из формулы (3.1) определим :

Диаграммы представлены в приложении.

3.2 Определение минимального радиуса вращения кулачка

Величину начального радиуса кулачка можно получить графически, строя диаграмму перемещения в функции от аналога углового уско­рения . По оси абсцесс откладываем значения аналога углового ускорений по оси ординат величину угла подъема, которые берем соответственно с диаграммы аналога углового ускорения и диаграммы угла подъема. После этого проводи под углом 60° к оси абсцесс прямую так, чтобы она касалась снизу одной из ветвей диаграммы с отрицательными абсциссами. Отрезок О₁А₀, который отсекает эта прямая на отрицательном направлении оси ординат определяет искомую величину r_min, т.е. такое значение r, при котором радиус кривизны профиля хотя бы в одной точке обращаясь в ноль, но отрицательных значениях иметь не может.

3.3 Построение профиля кулачка по закону движения

Строим диаграмму аналога углового ускорения. Для этогов прямоугольной системе координат по оси абсцесс откла­дываем отрезок L соответствующий одному обороту кулачка и делим эго на части, соответствующие фазовым углам. По оси координат откладываем значения аналога углового ускорения .

Затем по заданному виду и найденным параметрам, строим диаграмму аналога углового ускорения ().

Теперь строим диаграмму аналога угловой скорости. Аналог углового ускорения представляет собой производную от аналога угловой скорости по обобщенной координате, т.е. по углу поворота кулачка . Поэтому диаграмма аналога угловой скорости может быть получена путем графического интегрирования (операция обратная графическому дифференцированию) диаграммы аналога углового ускорения.

Отрезок, соответствующий фазе подъема делим на n равных частей, n=5, присваивая точкам деления номера от 0 до 5; отрезок, соответствующий фазе опускания, делим тоже на 5 равных частей и точкам деления присваиваем номера от 0 до 5’. Деление отрезков, соответствующих верхнему и нижнему выстою производим, учитывая неизменность рассматриваемых функций на этих отрезках.

Найдем точки 1”, 2”, 3” и т.д. на оси ординат получим, проводя горизонтальные линии из точек диаграммы аналога ускорения, лежащих в середине отрезков , , 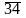и т.д. по оси абсцесс.

На отрицательном направлении оси абсцесс (влево от начала координат) отмечаем точку Р - полюс интегрирования на рас стоянии Н (мм) от начала координат и проводим отрезки Р – 1”, Р – 2”, Р – 3” и т.д.

На оси ординат диаграммы аналога скорости - s’ отмечаем точку 0’ (на чертеже совпадает с началом координат) и проводим отрезок параллельно отрезку , после этого строим отрезок 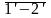параллельно отрезку и т.д.

Соединяя точки 0, 1, 2, ... плавной линией, получим искомую диаграмму аналога угловой скорости.

Строим диаграмму угла подъема. Она получается путем графического интегрирования диаграммы аналога угловой скорости. Все построения аналогичны построениям диаграммы аналога угловой скорости.

В качестве самоконтроля при построении диаграммы угла подъема необходимо учесть, что ордината, соответствующая концу фазы подъема, должна давать (приближенно) значение хода коромысла, ордината, полученная в конце фазы опускания, должна (приближенно) равняться нулю.

Задача построения профиля кулачка решается в общем случае при помощи метода обращения движения, когда всему механизму мысленно придаем вращение вокруг центра вращения кулачка О₁ с угловой скоростью  равной, но противоположно направленной угловой скорость кулачка. Кулачок тогда становиться неподвижным. Движение коромысла раскладываете на переносное движение вместе со стойкой и относительное движение относительно стойки.

Таким образом, сначала по данному значению угла _i строим положения коромысла в обращенном движении, затем, зная из диаграммы перемещения координату _i определяющую положение выходного звена относительно стойки находим по­ложение выходного звена и, следовательно, точку касания ролика коромысла с профилем кулачка.

Построения проводим в такой последовательности:

1) Строим отрезок О₁О₂=l₀ и проводим окружность этим радиусом с центром в точке О₁ и окружность радиусом r₀=r+r_рол. Проводим дугу радиуса О₂А=l₂ с центром в точке О₂ (траекторию центра ролика – точки А). Точка пересечения этой дуги с окружностью радиуса r₀ дает начальное положение коромысла А₀;

2) Пользуясь диаграммой = () производим разметку траектории центра ролика, т.е. указываем положение точек А_i.

3) Строим траекторию точки О₂ в обращенном движении, т.е. окружность радиуса l₀, начиная от точки О₂ в направ­лении противоположном вращению кулачка, разбиваем на дуги, соответствующим фазовым углам _П, _ВВ, ₀. Первую из этих дуг разбиваем на 5 равных частей, обозначая точки деления через 1, 2, ..., 5. Дугу, соответствующую фазе опускания делим на 5 равных частей, обозначая точки деления через 1^’, 2^’, .... 5^’;

4) Точки а_i на центровом профиле кулачка получаем как точки пересечения окружности радиуса О₂А₀ с центром в точке О₂ и окружности, центр которых совпадает с точной О₁ и которая проходит через точку А_i;

5) Проведя через точки а_i плавную линию, получаем центровой профиль кулачка;

6) Конструктивный профиль кулачка получаем как огибающую семейства;

7) Строим окружности радиуса r_рол с центрами на центровом профиле.

Таким образом из построения получаем:

R_min=81мм;

R_рол=16мм;

а_w=124мм;

β₀=40⁰.

Заключение

В курсовом проекте внимание уделено синтезу механизма и его динамическому расчету. А также подробно изложен ход решения и наглядно показаны схемы исходного механизма, зубчатой передачи, планетарной передачи, профиля кулачка.

Курсовой проект выполнен с учетом норм оформления технической документации и представлен в виде пояснительной записки.

Список используемой литературы

1. Артоболевский И.И. Теория механизмов и машин. – Ленинград, 1988.

- 640 с.

1. Артоболевский И.И., Эдельштейн Б.В. Сборник задач по теории механизмов и машин.- Ленинград,1973.- 256 с.

2. Кореняко А.С., Курсовое проектирование по теории механизмов и машин.-М.:Высшая школа, 1970.- 336 с.

3. Подоляк Н.Я. Синтез привода механизма. Методическое указание к выполнению курсового проекта по ТММ для студентов очного и заочного обучения специальностей 1201, 1502. –Орск: ОГТИ, 2003- 32 с.

4. Подоляк Н.Я. Синтез кулачкового механизма. Синтез привода механизма. Методическое указание к выполнению курсового проекта по ТММ для студентов очного и заочного обучения специальностей 1201, 1502.-Орск: ОГТИ, 2003.- 30 с.