2 Синтез привода механизма

2.1 Расчет планетарной ступени

Передаточное отношение от колеса 4 к водилу Н при неподвижном колесе 5 определяется по формуле:

(2.1)

Этой формуле соответствуют значения <25. Конструктивно принимаем =0,1. Число зубьев одного из зубчатых колес принимаем z₄=80.

Для подбора чисел зубьев колес 1, 2, 3 пользуюсь условием «3С» - сборки, соседства, соосности.

1. Условие соосности:

Учитывая что , приведем предыдущее уравнение к виду:

. (2.2)

Принимаем, что разность чисел зубьев сателлитов составляет 2 зуба,тогда

(2.3)

Теперь найдем число зубьев :

Преобразуем уравнение (2.1)

Уравнение (2.2) приведем к виду:

.

Составим систему уравнений:

,

Решая эту систему, определили, что

Условие выполнено.

2.Условие соседства:

, (2.3)

где K – количество сателитов (от 1 до 7).

3.Условие сборки:

, (2.4)

где N – любое натуральное число

К – число сателлитов

Определим размеры зубчатых колес:

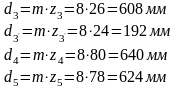(2.5)

Согласно полученным значениям вычерчиваю схему в масштабе.

Построим треугольник распределения скоростей для каждого из колес редуктора.

Отложим скорость точки А вправо. Соединим точку А с О и получим треугольник скоростей для колеса 4.

Проведем горизонталь из точки С оси. Получим скорость 5 колеса.

Проведем горизонталь из точки О₃, соединим ее с прямой проходящей через точки А и С.Получили точку О_3' и нашли скорость колеса 3'. Соединив точку О₃ и точку , получим треугольник скоростей для водила.

По построенным треугольникам скоростей можно определить передаточное отношение редуктора.

(2.6)

Все описанные построения приведены в приложении 2.

2.2 Синтез зубчатой цилиндрической передачи эвольвентного профиля

2.2.1 Определение размеров зубчатого зацепления

Размеры колес, а также всего зацепления, зависит от числа зубьев колес z_к=32, z_ш =16, от модуля зацепления m=5, общего для обоих колес, а также от метода их обработки.

Определяем геометрические размеры цилиндрической зубчатой передачи.

1. Шаг зацепления по делительной окружности

_Р =

2. Радиусы делительных окружностей

r_к =

r_ш =

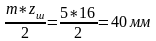
3. Радиусы основных окружностей

r_вк= r_к*cos

r_вш = r_ш* cos

4. Коэффициент суммы смещений

X

X_k=0

X_ш=0,06

5. Толщина зуба по делительной окружности

S_ш =

_Sк =

6. Угол зацепления:

ά_wш=20^o25^|

B=1000*X_∑/Z_∑=1,25

ά_wк=ά=20^o

7. Межосевое расстояние

а_w=

8. Коэффициент воспринимаемого смещения

у=

9. Коэффициент уравнительного смещения

10. Радиусы окружностей впадин

r_fк=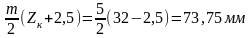

r_fш=

11. Радиусы окружностей вершин

r_ак=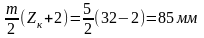

r_аш=

12. Радиусы начальных окружностей

r_wк=

r_wш=

13. Глубина захода зубьев

h_d=

14. Высота зуба

h=1.25m=1,25*5=6,25мм

Подсчитав все размеры элементов зацепления по формулам, приведенным выше, приступаем к вычерчиванию зубчатого зацепления. Определяем активную часть линии зацепления, затем строим рабочие участки профилей зубьев. Те участки профилей зубьев, которые участвуют в зацеплении, называют рабочими. Схема эвольвентного зацепления представлена в приложении…