1.1.6 Определение момента инерции маховика

Момент инерции маховика определим по формуле:

, (1.9)

где – максимальный момент инерции;

, (1.10)

где δ – неравномерность хода;

ΔJ_пр – изменение приведенного момента инерции механизма;

, (1.11)

ΔТ' – изменение кинетической энергии;

, (1.12)

Примем радиус маховика за 0,8 м, тогда его масса равна:

1.2 Динамический анализ механизма

1.2.1 Определение истинного закона движения механизма

Для определения истинного закона движения рассмотрим дифференциальное уравнение движения, которое имеет следующий вид:

(1.13)

где – приведённый момент сил сопротивления;

– приведённый момент сил движущих;

угловое ускорение ведущего звена;

угловая скорость вращения ведущего колеса;

– момент инерции;

– изменение момента инерции от угла поворота.

Момент инерции машинного агрегата находим по формуле:

(1.14)

Полученные значения производной сведём в таблицу 1.5.

Таблица 1.5 Значения производной приведённого момента инерции.

Положение	1	2	3	4	5	6	7	8	9	10	11	12
Јпр, кг/м2	1.43	1.7	0.82	-1.4	-2.26	-0.36	2.54	2.33	-1.8	-1.34	1.76	0.08

Решается дифференциальное уравнение методом последовательных приближений с помощью начальных условий. В основу решения положена формула равноускоренного движения. Полагаем, что в пределах достаточно малого угла поворота машина движется равноускоренно. Тогда, используя начальные условия, получим

Зная , определяются

Зная определяем .

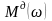Из дифференциального уравнения выражаем ε_i .

Зная ε_i , можно найти ω в следующем положении

Расчет вести до установившегося движения, то есть когда закон движения из цикла в цикл повторяется. Полученные значения представлены в приложении …..

1.2.2 Построение планов ускорений

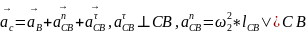
В результате определения истинного закона движения видим, что угловая скорость ω₁ при установившемся движении изменяется в зависимости от времени.

Скорректируем вычисленные ранее угловые скорости ω₂, ω₃, ω₄ относительно ω₁ для 1 положения:

=

где 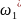– скорректированная угловая скорость, после определения истинного закона движения,

– поправочный коэффициент.

;

;

.

Для построения планов ускорений воспользуемся значениями , , .

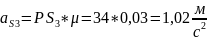
Скорректируем вычисленные ранее угловые скорости ω₂, ω₃, ω₄ относительно ω₁ для 2 положения:

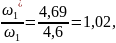
где – скорректированная угловая скорость после определения истинного закона движения,

– поправочный коэффициент.

;

;

.

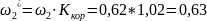Для построения планов ускорений воспользуемся значениями , , .