3.4 Енергетичний спектр електронів у кристалі. Модель Кроніга-Пенні

Для знаходження енергетичного спектра електронів у кристалі необхідно розв’язати одноелектронне рівняння Шредінгера (3.2) з періодичним потенціалом решітки . Власні функції і власні значення цього рівняння значною мірою залежать від виду періодичного потенціалу. Точний розв’язок рівняння Шредінгера можна знайти, коли потенціал має вигляд послідовних прямокутних бар’єрів (модель Кроніга-Пенні). Розглянемо елементи моделі на прикладі одновимірного кристала, в якому його потенціальне поле для простоти замінюється лінійним періодичним ланцюжком потенціальних бар’єрів шириною b, що чергуються з прямокутними потенціальними ямами шириною а. Період такої решітки a+b (рис. 3.4). Висота кожного бар’єра .

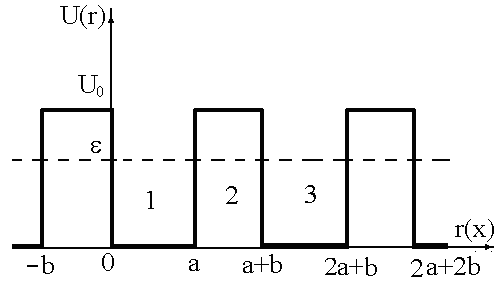
Рисунок 3.4 - Залежність потенціальної енергії електрона від міжатомної відстані в моделі Кроніга-Пенні для одновимірного кристала

Рівняння руху електрона в такому кристалі також описується рівнянням Шредінгера

,

де - хвильова функція електрона; - стала Дірака (h- стала Планка).

Розв’язок даного рівняння будемо шукати у вигляді функції Блоха , де - функція координат, яка не залежить від хвильового вектора і є періодичною з періодом решітки, тобто

.

Після підстановки функції Блоха рівняння Шредінгера набуде вигляду

.

Розглянемо три області і для кожної запишемо рівняння Шредінгера.

Область 1. (0 а, U(x)=0):

,

, де . (3.6)

Розв’язок (3.6) можна записати так:

; . (3.7)

Область 2. :

,

, де . (3.8)

Розв’язок (3.8) має такий вигляд:

. (3.9)

Область 3. фізично еквівалентна області 1 і тому для обчислення необхідно скористатися теоремою Блоха, згідно з якою хвильова функція, як і періодичний потенціал, задовольняють умови періодичності.

Для обчислення сталих інтегрування А, В, С і D необхідно скористатися граничними умовами та умовою неперервності та її першої похідної, тобто роз’язати систему рівнянь:

У загальній формі її можна записати як систему чотирьох лінійних однорідних рівнянь з чотирма невідомими:

. (3.11)

Умовою існування розв’язку системи є рівність нулю детермінанта ( ), складеного із коефіцієнтів при невідомих. Якщо визначник системи (3.11) то і постійні А, В, С і D = 0.

Після розкриття визначника четвертого порядку одержуємо

. 3.12)

Останнє рівняння зв'язує величини і , які містять власні значення енергії електрона з хвильовим вектором k. Отже, рівність (3.12) можна розглядати як співвідношення між і k. Розв'язати рівняння (3.12) складно. Тому в моделі вводять додаткові умови, що її спрощують. Розглянемо згідно з Кронігом та Пенні високі ( ) та тонкі ( ) бар'єри, але такі, що добуток є скінченним і сила потенціального бар’єру . Це означає, що , тоді із однаковими темпами. Оскільки , то

.

Проведемо оцінку :

~ , оскільки

.

Таким чином, .

При малих значеннях - гіперболічні величини ~1, а ~ .

Якщо врахувати, що << , , >> і << , то співвідношення (3.12) перепишеться так:

. (3.12')

Можна подати і так:

. (3.12'')

Введемо параметр Г, позначивши множник =Г>0.

Зазначимо, що згідно з означенням величина Г є мірою ефективної площі кожного бар'єра, тобто характеризує ступінь прозорості бар'єра для електрона або ступінь зв'язаності електрона в потенціальній ямі. Тоді рівняння (3.12''), з урахуванням , записують у вигляді

Г . (3.12''')

Оскільки є парною функцією (заміна k на -k не змінює рівняння), то із співвідношення (3.12''') випливає, що енергія електрона є також парною функцією від k: (k)= (-k). Рівняння (3.12''') розв’язується графічним методом. Точки перетину Г і (рис. 3.5) є корені (3.12'''). Бачимо, що кожному значенню хвильового числа k відповідає декілька значень енергії, оскільки .

Якщо розглядати всю сукупність електронів, то спектр їх хвильових чисел забезпечує межі зміни від -1 до

1.Тоді розв’язками рівняння (3.12''') будуть не окремі точки, а інтервали енергії , і т.д., які одержали назву енергетичних зон.

Рисунок 3.5 - Графічний розв`язок рівняння (3.12'''). Дозволені значення замальовані

Ліва частина рівняння (3.12''') зображена суцільною лінією. Оскільки може набувати значення в інтервалі [-1,1], то дозволеними значеннями є такі, для яких ліва частина рівняння (3.12''') не виходить за вказані межі. На рис 3.5 інтервали дозволених значень замальовані . Ширина цих інтервалів залежить від Г: із зменшенням Г їх ширина зростає. Крім того, ширина інтервалів залежить також від : якщо Г фіксоване, то ці інтервали збільшуються із зростанням .

Із співвідношень (3.7) та (3.9) випливає, що такі самі висновки стосуються енергії. Відтак, енергія електрона в полі періодичного потенціалу не може набувати довільних значень: існують зони дозволених та заборонених значень енергії.

Проаналізуємо, як змінюватиметься спектр електронів у двох граничних випадках: і . Випадок відповідає умові , тобто майже вільному електрону (наближення слабкого зв'язку). Із співвідношення (3.12''') отримаємо , тобто , і оскільки енергія є парною функцією хвильового числа , із співвідношення (3.7) отримують такий вираз для енергії електрона:

. (3.13)

Цей вираз збігається із залежністю (k) для вільних електронів.

В іншому граничному випадку (при ) бачимо, що . Фізично це означає, що електрон локалізований у нескінченно глибокій ямі, тобто є сильно зв'язаним (наближення сильного зв'язку). При з рівняння (3.12''') отримаємо , тобто , де і т.д.

З умови (3.9) отримаємо

. (3.14)

Отже, при система енергетичних зон вироджується у систему рівнів.