§ 3. Два види руху. Аналітичне задання руху

Будемо говорити, що перетворення площини зберігає орієнтацію площини, якщо репер R і його образ однаково орієнтовані і змінює орієнтацію площини, якщо R і протилежно орієнтовані.

Наприклад, такі добре відомі із школи рухи як паралельне перенесення та поворот навколо точки зберігають орієнтацію площини, а осьова симетрія змінює орієнтацію площини.

Коли рух орієнтація площини не змінює, то він називається власним (рухом першого роду), якщо змінює – невласним (рухом другого роду).

Отримаємо аналітичне задання руху.

Нехай g – даний рух. Розглянемо на площині ортонормований репер R= . Позначимо (х, у) координати довільної точки М в цьому репері, а через ( ) координати її образа при рухові g в цьому ж репері R .

Одержати аналітичне задання руху значить виразити координати точки в репері R через х, у.

Так як рух g задано, то за теоремою 2 ортонормований репер R= перейде в ортонормований репер . , причому .

Отже, фактично одержуємо звичайну задачу перетворення прямокутних систем координат: точка в старому репері R має координати , а в новому репері  – х, у. Потрібно виразити через х, у.

Такі формули мають вигляд:

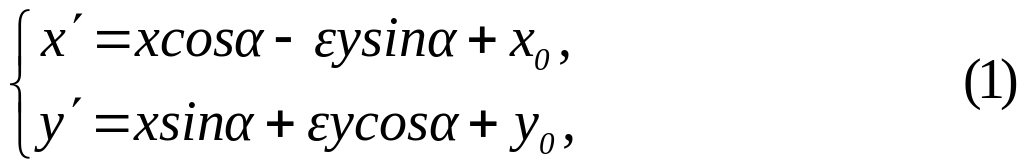
де , якщо репери і однаково орієнтовані, тобто при рухах першого роду, і , при рухах другого роду.

§ 4. Класифікація рухів площини

Класифікацію рухів площини проведемо в залежності від наявності інваріантних точок і прямих, і одержимо аналітичне задання конкретних рухів.

Інваріантна точка (нерухома) перетворення – це точка, яка переходить в себе при даному перетворенні.

Інваріантна пряма (нерухома) – це пряма, кожна точка якої переходить в точку цієї ж прямої при даному перетворенні .

Власні рухи:

а) тотожне перетворення. Ясно що при такому перетворенні повороту немає, отже і перенесення немає, тому . Підставивши ці значення в формулу (1) отримаємо :

. Тобто інваріантними залишаються всі точки і всі прямі площини.

б) поворот на . Нехай центром обертання є точка О(0,0). Тоді , і маємо аналітичне задання :

Інваріантною є єдина точка – точка навколо якої виконується обертання. Інваріантних прямих немає.

в) центральна симетрія. Тут . Нехай центром симетрії є точка О(0,0), тоді . Отримаємо з формул (1) аналітичне задання такої симетрії:

Інваріантна точка – центр симетрії. Інваріантні прямі – прямі, що проходять через центр симетрії.

г) паралельне перенесення. Маємо Аналітичне задання:

Інваріантних точок немає, інваріантні прямі – прямі, що паралельні до .

Невласні рухи:

а) осьова симетрія. Повороту немає, тому . Якщо , то отримаємо осьову симетрію відносно осі ОХ:

Інваріантні точки – всі точки вісі симетрії. Інваріантні прямі – сама вісь симетрії і всі прямі, які перпендикулярні до неї.

б) ковзна симетрія (симетрія відносно прямої, а потім перенесення на паралельний до цієї прямої).

Тут , і якщо розглянути осьову симетрію відносно вісі ОХ, то отримаємо :

Інваріантні точки – точки вісі симетрії, інваріантна пряма – вісь симетрії.