§ 31. Циліндричні поверхні

Поверхня, яка разом з будь-якою своєю точкою містить і всю пряму, яка проходить через цю точку, паралельно до деякого вектора називається циліндричною.

Циліндричну поверхню можна отримати, якщо провести через деяку криву (направляючу) прямі лінії (твірні), які паралельні до . Якщо паралельний до вісі OZ, то за направляючу можна взяти лінію, яка лежить в площині XOY. Тоді циліндричну поверхню можна задати рівнянням від двох змінних F(x,y)=0 – тобто направляючою. Дійсно, в цьому випадку, якщо точка належить циліндричній поверхні (її координати задовольняють рівняння F(x,y)=0), то цій поверхні буде належати і точка (так як її координати задовольнятимуть це ж рівняння F(x,y)=0) отже, поверхні буде належати і вся пряма, яка паралельна до вісі OZ.

Циліндр другого порядку може бути (в залежності від направляючої) еліптичним, гіперболічним, параболічним, а також виродженим циліндром, який розпадається на пару площин, що перетинаються, пару паралельних площин, пару площин що співпадають (див. §14).

Еліптичним циліндром називається поверхня, яка в деякі прямокутній системі координат визначається рівнянням:

. (28)

Дослідимо форму еліптичного циліндра методом перерізів і побудуємо його.

1). Розглянемо перерізи еліптичного циліндра площиною XOY і паралельними до неї площинами: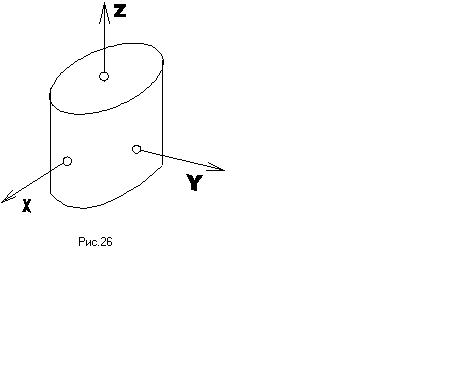

– еліпс.

2). В перетині еліптичного циліндра з площиною XOZ і паралельними до неї площинами отримаємо:

або

а). Якщо то маємо пару прямих, що співпали (будуємо пряму паралельну до вісі OZ) (рис 26).

b). Якщо маємо порожню множину.

с). Якщо отримаємо пару паралельних прямих (які паралельні до вісі OZ).

3). Перетин еліптичного циліндра з площиною YOZ і паралельними до неї площинами повністю аналогічний до попереднього (рис.26).

Як бачимо для побудови циліндра можна і не використовувати метод перерізів, а просто побудувати направляючу і провести твірні, паралельні до вісі циліндра (в нашому випадку до вісі OZ).

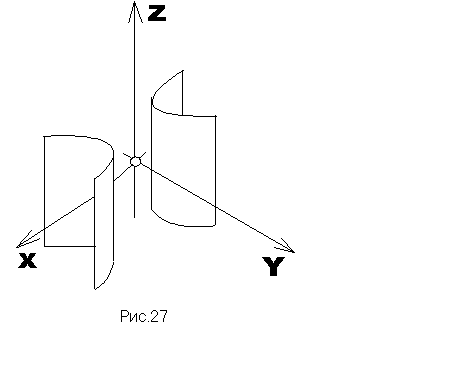
Гіперболічним циліндром (рис.27) називається поверхня, яка в деякі прямокутній системі координат визначається рівнянням:

. (29)

Параболічним циліндром (рис.28) називається поверхня, яка в деякі прямокутній системі координат визначається рівнянням:

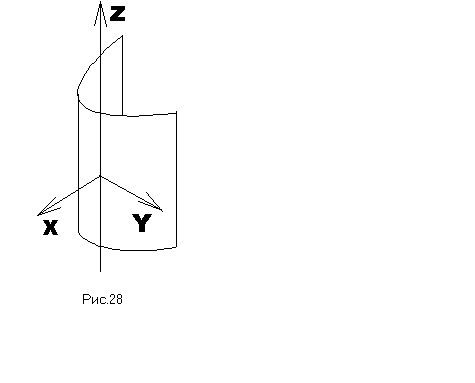. (30)

Приклад 10.

Побудувати зображення циліндричної поверхні, заданої рівнянням .

Розв’язання: Рівняння з двома змінними х і у визначає циліндричну поверхню, твірні якої паралельні до вісі OZ. За направляючу можна взяти лінію перетину поверхні з координатною площиною XOY.

Так як площина XOY має рівняння z=0, то направляюча задається системою рівнянь:

Щоб привести до канонічного вигляду рівняння виконаємо паралельне перенесення системи

к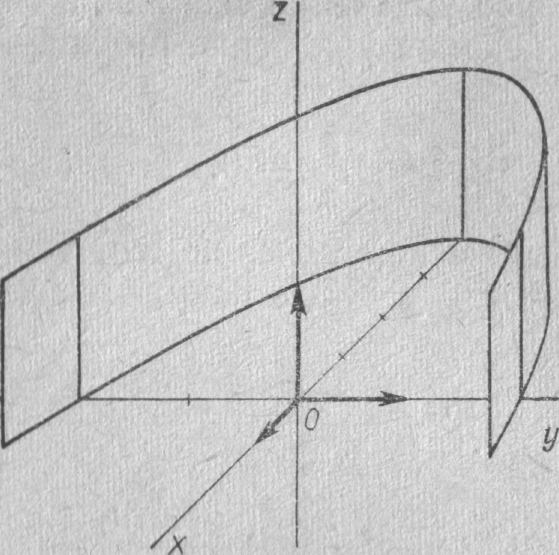 оординат за формулами:

при якому початок

координат переходить в точку

. У нових координатах

одержуємо систему рівнянь:

Така система рівнянь Рис.29

визначає параболу, у якої вершина

розташована в точці O', а вісь направлена по осі O'X', яка співпадає з віссю OX (рис.29). Для уточнення побудови корисно побудувати точки перетину цієї параболи з віссю OY. Для цього розв’яжемо систему рівнянь одержимо: . Відзначимо на малюнку точки і і проведемо через них направляючу параболу.

Щоб отримати наочне зображення, побудуємо ще одну параболу, утворену з направляючої паралельним перенесенням уздовж осі OZ. Проведемо ще декілька твірних, сполучаючи точки цих двох парабол, які розташовані на одній паралелі до осі OZ.