Лабораторная работа №1

Экспертная система « Дерево решений»

1. Цель работы:

Изучение возможностей и особенностей построения экспертной системы на основе метода дерева решений. Получение практических навыков в создании баз знаний (БЗ) с использованием проблемно-независимой инструментальной оболочки.

2. Теоретическая часть

При построении экспертных систем (вопросно-ответных сове­тующих систем), обобщающих опыт людей-экспертов в данной проблемной области, многие задачи решаются более эффективно, когда исходная задача Q разбивается на некоторое число подзадач Q₁, Q₂.. Q_к и делаются попытки решить каждую из них. Данный подход весьма актуален, в частности, при конструировании БИС и СБИС, содержащих сотни тысяч элементов, а также при использовании в задачах классификации, содержащих значитель­ное число признаков. Под решением задачи понимаются:

• нахождение оптимального решения;

• доказательство, что подзадача неразрешима;

• доказательство, что значение полученного решения хуже, чем предыдущее.

Такое разбиение обычно описывают деревом, где исходная за­дача моделируется корневой вершиной. Деревом называется связ­ный граф без циклов и обозначается Т=(Х, U). |Х|=n. где X - множество вершин, а U- множество ребер. Любое дерево Т имеет n-1 ребро. Начальная вершина, т.е. вершина с наименьшим номером, называется корнем, из которого выходят ребра, назы­ваемые ветвями дерева. Очевидно, что в дереве любые две вер­шины Х_i , Х_jсвязаны единственной цепью и в любом связном гра­фе G можно выделить некоторое дерево Т. Для задач конструирования значительный интерес представляют деревья, у которых число вершин равно числу вершин графа, из которого выделено это дерево. Такие деревья называются покрывающими. Для одного и того же связного графа можно выделить некоторое множество покрывающих деревьев.

Смысл разбиения задачи состоит в том, что после разбиения подзадачи легче решать, они имеют значительно меньший размер или имеют новую структуру. Очевидно, что если разбиение окончено, то множество подзадач, на которые разбита задача, долж­но представлять всю задачу. После окончания каждая подзадача представляется вершиной дерева, которая называется висячей. Важной проблемой является нахождение оптимального решения на основе перебора путей на дереве решений. Задачи такого типа называют поисковыми. А сам поиск связан с исследованием графовых структур. Существуют три основных типа поиска в зависи­мости от того, как выбираются вершины дерева для прохождения ветвления. Это поиск с возвращением, поиск в глубину и поиск в ширину.

Поиск с возвращением заключается в попытках расширить частное решение. На каждом шаге поиска, если расширение теку­щего частичного решения невозможно, происходит возврат к пре­дыдущему частичному решению и предпринимается попытка снова его продолжить. Другими словами, поиск с возвращением - это продолжение расширения исследуемого решения до тех пор, пока это возможно. Когда решение нельзя расширить, производится возврат назад и попытка сделать другой выбор на ближайшем шаге, где имеется такая возможность. Поиск с возвращением от­носится к классу экспоненциальных алгоритмов.

Поиск в глубину на дереве решений неформально как бы соот­ветствует "нырянию" в глубь дерева. Идея метода состоит в том, чтобы в каждой исследуемой вершине дерева выбирать один из возможных путей и исследовать его до конца, причем другие, существующие пути решений при этом не рассматриваются, пока сохраняется возможность получить конечный результат, исследуя выбранное направление. При поиске в глубину выбирается опре­деленный путь по дереву и производится его продолжение до по­лучения решения или до тех пор, пока дальнейшее продвижение окажется невозможным. Тогда процесс поиска возобновляется от ближайшей вершины дерева, имеющей смежные неисследованные вершины. Из сказанного следует, что при поиске в глубину пе­ребор сначала выполняется вдоль одного пути, пока не будет достигнута максимально возможная глубина. Далее рассматрива­ются другие пути такой же или меньшей глубины, которые отли­чаются от первого последним шагом, затем исследуются пути, отличающиеся последними двумя шагами и т.д. Процесс повторя­ется до получения требуемого результата. Основное достоинство методов поиска в глубину то, что большинство из них относится к классу полиномиальных алгоритмов и может быть в основном реализовано за время 0(n).

Основной недостаток поиска в глубину заключается в том, что при исследовании дерева решений с большой вероятностью можно пройти мимо той ветви, на которой раньше всего появля­ется окончательное решение.

Поиск в ширину. При использовании этого метода ветвления поиск происходит от уровня к уровню, причем если на уровне 1 начальная задача 0, разбивается на подзадачи Q₁, Q₂.. Q_к, то каждая из них исследуется раньше, чем задачи уровня 2. За­дачи в уровне, которые трудны для разрешения, разбиваются на подзадачи уровня 2 и процесс продолжается аналогично.

Поиск в ширину эффективно используется при установлении изоморфизма и изоморфного вложения графов при разбиении и размещении схем. Алгоритмы поиска в ширину в основном реали­зуются за время 0(n²)-0(n⁴).

Существует много процедур повышения эффективности поиско­вых методов. Основные из них - это упорядочивание ветвей, от­ходящих от каждой вершины так, что в первую очередь рассмат­риваются наиболее перспективные ветви, и движение вперед до поиска наилучшей из всех найденных, неза­висимо от того, где она расположена в дереве.

Многие задачи сводятся к значительному перебору вариантов, приближающемуся к полному. В некоторых случаях полный перебор удается заменить перебором с отсечениями. Наиболее употреби­тельным в этой связи является метод ветвей и границ. Ме­тод основан на переборе определенных вариантов решений задачи при условии, что число этих вариантов конечно. При этом в об­щем случае полный перебор заменяется частичным, так как используются априорные оценки вариантов, позволяющие отбрасы­вать "неперспективные" решения. Метод ветвей и границ состоит из операций ветвления и отсечения. Операцию ветвления можно осуществить на основе методов поиска как в глубину, так и в ширину.

Отсечение вариантов решения задачи выполняется с помощью оценочной функции, которая задается на вершинах дерева перебора и дает верхнюю или нижнюю границу значений функции для вариантов решений, входящих в множество Q. Оценочная функция. Дающая нижнюю границу в процессе разбиения множества, не убывает, а оценочная функция с верхней границей не возрастает. Точность оценки зависит от способа разбиения множества Q. Существует три основных способа отсечения ветвей:

• по результатам сравнения текущего значения с уже найденным;

• по результатам сравнения двух оценок;

• прекращение ветвления в вершине, не содержащей опти­мального решения.

Порядок продолжения ветвления выбирается на основе после­довательного построения ветвей или по минимальной нижней (максимальной верхней) границе или на основе их комбинаций. Процедура ветвления и отсечения повторяется до получения оп­тимального или квазиоптимального (с заданной точностью) реше­ния. Учитывая специфику рассматриваемой задачи, вычислить границы целевой функции нужно как можно ближе к оптимальному значению. Это определит число ветвящихся вершин и соот­ветственно степень сокращения перебора при решении задачи.

В данной лабораторной работе реализован один из методов поиска по дереву решений (модифицированный поиск в глубину), который используется при проектировании экспертной системы и создании базы знаний. Практическая реализация экспертной системы (подготовка базы знаний и ее использование) не требует знания какого-либо алгоритмического языка программирова­ния, поскольку так называемая проблемно-независимая программ­ная оболочка уже реализована на языке С++ в среде Borland для IВМ РС.

Экспертная система состоит из двух программ: подготови­тельной и исполнительной. При работе с каждой из них на экра­не появляется основное меню, с помощью которого производится выбор необходимой процедуры. Подготовительная программа поз­воляет эксперту сформировать базу знаний, а исполнительная программа дает возможность пользователю, используя уже гото­вую базу знаний, реализовать возможности экспертной системы в определенной проблемной области. В результате реализации пер­вой программы создается файл базы знаний, модификация которого в процессе реализации второй программы невозможна. Таким образом, процессы создания и использования экспертной системы программно изолированы. Связующим элементом между ними явля­ется хранящийся на диске файл базы знаний.

В нашем случае база знаний имеет вид ветвящегося дерева, по которому можно двигаться вниз, каждый раз выбирая новое усло­вие. Движение всегда заканчивается каким-либо логическим вы­водом.

Такая экспертная система работает следующим образом. Нап­ример, человек приходит в отдел кадров, садится за персональ­ный компьютер и отвечает на вопросы, последовательно возникающие на экране:

Код пути

1 - Есть диплом о высшем образовании

1-2 Нет изобретений

1-2-1 Средний балл в ведомости, прилагаемой диплому, более 4

1-2-1-1 Экспертная система делает вывод: "Принять на работу инженером".

Можно сказать, что отвечая на вопросы, мы прошли три уров­ня ветвей от корневой вершины (главную ветвь, вторую и третью). В данном варианте реализации базы знаний возможно наличие до 5 главных ветвей, отходящих от корневой вершины, а исходящих ветвей от остальных вершин - до 4. Здесь предусмот­рены 5 уровней ветвей в глубину и 6-й уровень выводов. Нумерация исходящих ветвей в вершинах осуществляется слева напра­во для каждой родительской вершины. В качестве примера приведен фрагмент базы знаний E₁, содер­жащей 2 главные ветви и по 2 исходящих ветви в вершинах. Если набрать код пути 1-2-2-1-1. то на экране увидим:

Код пути

Главная ветвь - 1 - Есть диплом о высшем образовании

2-я ветвь - 1-2- Нет изобретений

3-я ветвь - 1-2-2 - Средний балл диплома <4

4-я ветвь - 1-2-2-1- Стаж менее 2-х лет

5-я ветвь - 1-2-2-1-1 -

Вывод:- 1-2-2-1-1 - В приеме на работу отказать

Код пути для каждой ветви состоит из номеров последовательно пройденных ветвей (вершин), начиная от корневой вершины. Для предыдущего примера в левом столбце также указан код пути до получения логического вывода, который (за исключением 2-й ветви) пролег по крайнему левому маршруту дерева.

3. Порядок выполнения работы

Получить у преподавателя вариант задания.

Ознакомившись с теоретическим разделом и пояснениями к программам, реализовать базу знаний в выбранной проблемной области.

При выполнении работы следует руководствоваться основным меню подготовительной программы (п.3.1, п.3.2), изображенном на рисунке 1.

Рисунок 1. Основное меню подготовительной программы

3.1. Основное меню подготовительной программы:

- пояснения;

- задание количества главных и количества исходящих ветвей;

- просмотр правил;

- ввод и редактирование правил;

- вызов правил с диска;

- запись правил на диск;

- вывод правил на принтер;

- задание названия базы знаний;

- выход.

Выбор необходимой процедуры осуществляется путем нажатия соответствующей цифры на клавиатуре.

1 - При создании новой базы знаний необходимо задать пределы ветвления (Рисунок 2). На экране появляются запросы:

"Сейчас количество главных ветвей 0.

Введите количество главных ветвей (1-5) ".

"Сейчас количество исходящих ветвей в вершинах 0.

Введите количество исходящих ветвей (2-4)".

Рисунок 2. Задание количества главных и исходящих ветвей

После выбора нужного количества главных и исходящих ветвей необхо­димо нажать клавишу «Принять».

2 - Правила из нужной базы знаний можно просмотреть (Рисунок 3).

Рисунок 3. Просмотр правил

На экране появляется запрос: "Введите код пути". При этом цифры кода пути задаются в соответствии с пожеланиями пользователя, в диапазоне от 1 до n, где n -заданное количество главных и исходящих ветвей дерева решений. После задания кода пути и фиксации данного пути на экране появляются соответствующие выбранному коду правила. Например:

1-есть диплом

1-1 - есть изобретения

1-1-1- стаж >2 лет

1-1-1-1 - член профсоюза

5-я ветвь - вывод: "Принять МНС".

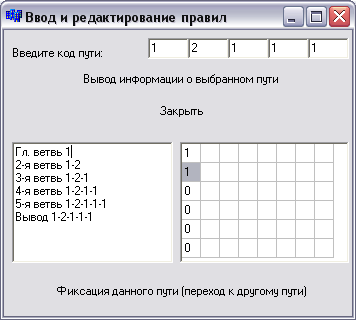
Рисунок 4. Ввод и редактирование правил

Для возврата в основное меню нажать клавишу «Закрыть».

3 - При создании новой базы знаний, либо при редактировании уже имеющейся, существует возможность изменения и созда­ния правил. На экране появится запрос: "Введите код пу­ти".

После задания необходимого кода на экране появится набор строк, каждая из которых соответствует правилу для выбранного пути. 6-я строка заключает в се­бе вывод, который должна сделать ЭС в этом случае. Фиксация данного пути и возврат в основное меню производится нажатием клавиши «Закрыть».

4 - В случае, если уже имеется готовая база знаний, ее можно вызвать для работы с программой. На экране высвечи­ваются все имена файлов, находящихся в данной директо­рии.

Рисунок 5. Окно для открытия имеющейся базы

При этом необходимо выбрать (выделить) нyжную базу знаний (из числа указанных на экране) и нажать кла­вишу «Открыть». После чего можно продолжать работу с конкретной базой знаний.

5 - После создания либо изменения базы знаний необходимо записать ее для дальнейшего использования с исполни­тельной программой. На экране появляется запрос (см. Рисунок 6): «Сохранить как»

Введите имя файла, его расширение (.bz) и нажмите клавишу «Сохранить».

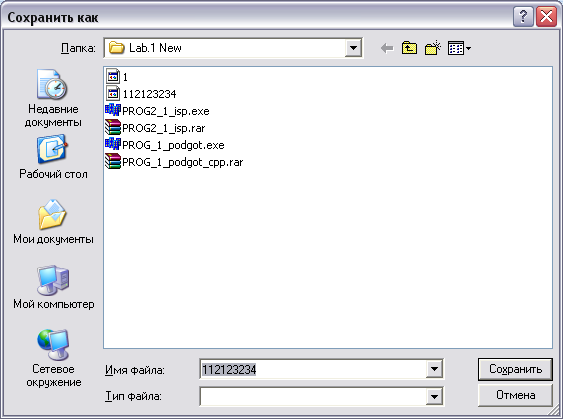
Рисунок 6. Сохранение созданной базы

6 - После создания или редактирования БЗ необходимо присвоить ей имя. На экране появляется запрос: «Введите название базы знаний».

Рисунок 7. Задание названия базы знаний

Введите название и нажмите клавишу «Принять». В дальнейшем при работе с этой БЗ на экране будет появляться заданное название.

7 - Выход из подготовительной программы.

3.2. Основное меню исполнительной программы

Рисунок 8. Исполнительная программа

- пояснения;

- вызов правил с диска;

- реализация экспертной системы;

- выход.

1 – Необходимо вызвать правила с диска.

При нажатии на этот пункт открывается директория, в которой ранее сохранялась подготовительная база.

Нужно выбрать необходимую базу и нажать клавишу «Открыть».

В случае, если нужная БЗ находится в другой директории, необходимо скопировать ее.

2 - На экране высвечиваются возможные варианты ответов. Путем установки курсора на нужную строку и нажатием кла­виши «Выбрать» фиксируются нужные ответы.

3 - Запустить на решение исполнительную программу.

Убедиться в работоспособности экспертной системы и объяснить полученные результаты.

4. Содержание отчета

Цель работы.

Краткая теоретическая часть.

Вариант задания.

Графическое изображение дерева решений.

Распечатки результатов работы.

Выводы.