8. Оформити звіт.
Індивідуальне завдання: виконати відповідне варіанту завдання (перевірити гіпотезу про рівність дисперсії середньої тривалості життя значенню =70.
Лабораторна робота № 22(2)
Тема
Перевірка гіпотез про математичні сподівання нормального розподілу .
Мета
Уміти
проводити перевірку гіпотез 
про
математичні сподівання нормального
розподілу генеральної сукупності.
Теоретичні відомості
Опрацювати матеріал Лекції № “ Гіпотези про параметри нормального розподілу генеральної сукупності”.
Практичне правило перевірки нульової гіпотези.
При
заданому рівні значущості
перевірку
нульової гіпотези 
про
рівність математичних сподівань двох
нормально розподілених сукупностей з
невідомими, але однаковими дисперсіями
за малими незалежними вибірками проводять
за схемою :
1. Одним
із методів знаходять вибіркові середні
і
виправлені дисперсії
і 
.
2. Обчислюють спостережуване значення критерію
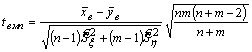
1. А) Альтернативна гіпотеза .
З
таблиці критичних точок розподілу
Стьюдента (двостороння критична область)
за рівнем значущості
і
числом ступенів вільності 
знаходять
критичну точку
.
Якщо - нульову гіпотезу приймають.
Якщо 
-
нульову гіпотезу відхиляють.
b)
Альтернативна гіпотеза
.
З таблиці критичних точок розподілу Стьюдента (одностороння критична область) за рівнем значущості і числом ступенів вільності знаходять критичну точку правосторонньої критичної області .
Якщо - нульову гіпотезу приймають.
Якщо - нульову гіпотезу відхиляють.
c)
Альтернативна гіпотеза
.
Знаходимо критичну точку як в пункті b).
Якщо - нульову гіпотезу приймають.
Якщо - нульову гіпотезу відхиляють.
Зауваження
Якщо ж невідомо чи дисперсії однакові, то перш ніж порівнювати математичні сподівання потрібно за критерієм Фішера-Снедекора попередньо перевірити гіпотезу про рівність дисперсій.
В даній лабораторній роботі будемо використовувати наступні функцій:
СРЗНАЧ (AVERAGE) — повертає середнє арифметичне аргументів.
Синтаксис: AVERAGE(число1;число2;...)
Число1, число2, ... – це від 1 до 30 аргументів, для яких обчислюється середнє.
Зауваження
Аргументи мають бути або числами, або іменами, масивами або посиланнями, що містять числа.
Якщо аргумент, що є масивом або посиланнями, містить тексти, логічні значення або порожні клітинки, то такі значення ігноруються; але клітинки, які містять нульові значення, враховуються.
ДИСП(VAR) – обчислює дисперсію на основі вибірки.
Синтаксис: VAR(число1;число2;...)
Число1, число2, ... – це від 1 до 30 числових аргументів, які відповідають вибірці з генеральної сукупності.
ЕСЛИ(IF) Повертає одне значення, якщо задана умова при обчисленні дає значення ИСТИНА,та інше значення, якщо ЛОЖЬ.
Функція ЕСЛИ використовується при перевірці умов для значень і формул.
Синтаксис: ЕСЛИ(лог_выражение;значение_если_истина;значение_если_ложь)
Лог_выражение — це довільне значення або вираз, який набуває значення ИСТИНА абоЛОЖЬ.
Значение_если_истина — це значення , яке повертається, якщо лог_выражениедорівнює ИСТИНА. Значение_если_истина може бути формулою.
Значение_если_ложь — це значення , яке повертається, якщо лог_выражениедорівнює ЛОЖЬ. Значение_если_ложь може бути формулою.
СТЬЮДРАСПОБР (TINV) повертає t-значення для розподілу Стьюдента, як функцію ймовірності і числа ступенів свободи. Використовується для знаходження критичних значень t -розподілу.
Синтаксис
СТЬЮДРАСПОБР(вероятность;степени_свободы)
Вероятность — це ймовірність, пов’язана з двостороннім розподілом Стьюдента.
Степени_свободы — це число ступенів свободи.